 |
Применим арифметическое кодирование (реализация IBM).
|
|
|
|
Аналого-цифровое преобразование сигналов.
Реализация исходного аналогового сигнала во временной области:

динамический диапазон U =0÷10 В.
Общий вид спектра такого сигнала: 
Примем fmax равной 24,4 кГц, определим период и частоту дискретизации:
|
|
|
|
 ,
,
 -3 c,
-3 c,
 ,
,

Изображение дискретного сигнала:

Выберем число уровней квантования L равным 11. Определим шаг квантования Δ:


Выполним квантование полученных дискретных выборок по амплитуде. Для этого значение дискретной выборки будем присваивать одному из уровней квантования, при этом, если значение выборки меньше чем Δ/2, то выборку присваиваем меньшему уровню, если значение выборки больше или равно чем Δ/2, то выборку присваиваем большему уровню.

Найдем разрядность двоичного кода, требуемую для представления полученного многоуровневого квантованного сигнала в двоичном виде:


Таблица соответствия номера уровня двоичной комбинации:
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
Преобразуем ранее полученные квантованные выборки в двоичные комбинации, в соответствии с таблицей:
0100 0110 0110 0111 0111 1000 1001 1001 1001 1001 1001 1000 1000 1000 0111 0111 0111 0110 0111 1001 1001 1000.
Определение битовой скорости двоичного потока и объем информации, соответствующий выбранному количеству дискретных значений:

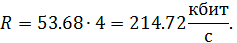
Рассмотрим дифференциальную импульсно-кодовую модуляцию сигнала (ДИКМ).
При данной модуляции передаются не текущие значения отсчетов, а разница между соседними отсчетами.
Разностный сигнал будет иметь следующий вид:
|
|
|

Если исходный сигнал имел динамический диапазон U 0÷10В, то сигнал, прошедший через ДИКМ, как видно, имеет динамический диапазон U -2÷4В. Уменьшение динамического диапазона позволяет уменьшить число уровней квантования до 6 при том же шаге квантования 1В.
Квантованный сигнал имеет вид:

Рассчитаем битовую скорость кодированного методом ДИКМ сигнала:


Сравним ее со скоростью, полученной при простой ИКМ:

За счет уменьшения уровней квантования, мы получили меньший объем передаваемой информации.
Вариант реализации АЦП.

Устройство собрано на PIC16F876A. Делители (R10-R19) определяют ширину диапазона. Подбор делителей на входе устройства позволяет измерять сигналы в широком диапазоне. Программно можно корректировать смещение сигнала +/- в случае погрешности номиналов сопротивлений делителя.
Точность измерения определяется по формуле:

Например, если делителями задан диапазон 10 В, то точность составляет
10 / 1023 = 0,0097 В
Кодирование источника, сжатие двоичной информации.
Рассмотрим алгоритм Шенона-Фано.
Для имеющейся последовательности
0100 0110 0110 0111 0111 1000 1001 1001 1001 1001 1001 1000 1000 1000 0111 0111 0111 0110 0111 1001 1001 1000
применим статистический алгоритм сжатия Шенона-Фано.
Определим статистику повторения комбинаций в последовательности:
| 0100 | 1 |
| 0110 | 3 |
| 0111 | 6 |
| 1000 | 5 |
| 1001 | 7 |
Построим дерево алгоритма

Полученная кодировка:
| 0100 | 011 |
| 0110 | 010 |
| 0111 | 11 |
| 1000 | 10 |
| 1001 | 00 |
Запишем исходную последовательность в новой кодировке:
011 010 010 11 11 10 00 00 00 00 00 10 10 10 11 11 11 010 11 00 00 10
Определим коэффициент сжатия:



Применим статистический алгоритм сжатия Хаффмана.
Определим статистику повторения комбинаций в последовательности:
| 0100 | 1 |
| 0110 | 3 |
| 0111 | 6 |
| 1000 | 5 |
| 1001 | 7 |
Построим дерево алгоритма:

Полученная кодировка:
| 0100 | 111 |
| 0110 | 110 |
| 0111 | 01 |
| 1000 | 00 |
| 1001 | 10 |
|
|
|
Запишем исходную последовательность в новой кодировке:
111 110 110 01 01 00 10 10 10 10 10 00 00 00 01 01 01 110 01 10 10 00
Определим коэффициент сжатия:



Применим арифметическое кодирование (реализация IBM).
Кодирование происходит по следующему алгоритму: каждому символу сопоставляется его вес: вначале он для всех равен 1. Все символы располагаются в естественном порядке, например, по возрастанию. Вероятность каждого символа устанавливается равной его весу, деленному на суммарный вес всех символов. После получения очередного символа и постройки интервала для него, вес этого символа увеличивается на 1.
Рассчитаем вероятности получения следующего символа, с учетом пришедших ранее символов и границы отрезка.
| Номер итерации | Веса символов | Вероятность символа | Граница интервала | ||||
| 0100 | 0110 | 0111 | 1000 | 1001 | |||
| 1 | 1 | 1 | 1 | 1 | 1 | 1/5 | (0;1/5) |
| 2 | 2 | 1 | 1 | 1 | 1 | 1/6 | (2/30;3/30) |
| 3 | 2 | 2 | 1 | 1 | 1 | 2/7 | (16/210;18/210) |
| 4 | 2 | 3 | 1 | 1 | 1 | 1/8 | (69/840;70/840) |
| 5 | 2 | 3 | 2 | 1 | 1 | 2/9 | (626/7560;628/7560) |
| 6 | 2 | 3 | 3 | 1 | 1 | 1/10 | (3238/38800;3239/38800) |
| 7 | 2 | 3 | 3 | 2 | 1 | 1/11 | (35628/415800;35629/415800) |
| 8 | 2 | 3 | 3 | 2 | 2 | 2/12 | (427546/4989800;427548/4989800) |
| 9 | 2 | 3 | 3 | 2 | 3 | 3/13 | (2779059/16216200;2779062/16216200) |
| 10 | 2 | 3 | 3 | 2 | 4 | 4/14 | (12968952/75675600;12968956/75675600) |
| 11 | 2 | 3 | 3 | 2 | 5 | 5/15 | (48633580/283783500; 48633585/283783500) |
| 12 | 2 | 3 | 3 | 2 | 6 | 2/16 | (155627464/454053600; 155627466/454053600) |
| 13 | 2 | 3 | 3 | 3 | 6 | 3/17 | (1322833452/3859455600; 1322833455/3859455600) |
| 14 | 2 | 3 | 3 | 4 | 6 | 4/18 | (7937000720/23156733600; 7937000724/23156733600) |
| 15 | 2 | 3 | 3 | 5 | 6 | 3/19 | (37700753425/109994484600; 37700753428/109994484600) |
| 16 | 2 | 3 | 4 | 5 | 6 | 4/20 | (251338356171/733296564000; 251338356175/733296564000) |
| 17 | 2 | 3 | 5 | 5 | 6 | 5/21 | (1319526369902/3849806961000; 1319526369907/3849806961000) |
| 18 | 2 | 3 | 6 | 5 | 6 | 3/22 | (5805916027571/16939150628400; 5805916027574/16939150628400) |
| 19 | 2 | 4 | 6 | 5 | 6 | 6/23 | (4451202287810/129866821484400; 4451202287816/129866821484400) |
| 20 | 2 | 4 | 7 | 5 | 6 | 6/24 | (17804809151258/519467285937600; 17804809151264/519467285937600) |
| 21 | 2 | 4 | 7 | 5 | 7 | 7/25 | (74186704796326/2164447024740000; 74186704796333/2164447024740000) |
| 22 | 2 | 4 | 7 | 5 | 8 | 2/26 | (27550617814927/80393746633200000; 27550617814927/80393746633200000) |
| 23 | 2 | 4 | 7 | 6 | 8 | 6/27 | (371933340501547/24644094144309000000; 371933340501553/24644094144309000000 ) |
Возьмем число 371933340501550/24644094144309000000, принадлежащее последнему интервалу и переведем его в двоичный вид, в результате чего получим число
0.00000000000000000000000000000000000000000000001011010000100100011010000111111111100100111111101111



|
|
|


