 |
Канальное (помехоустойчивое) кодирование.
|
|
|
|
Код Хэмминга.
Используем код Хэмминга (7,4), т.е. блок длинной 7 символов, из которых 4 разряда – информационные и 3 – контрольные. Для построения блоков необходимо получить производящую матрицу G = (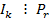
), где 
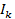- единичная матрица, а 
- матрица, столбцы которой задаются урвнениями:
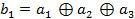
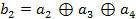
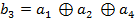
G=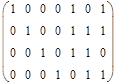 
Перемножая построчно G с блоком информационной комбинации и складывая затем строки по модулю 2, получаем кодовую комбинацию:
ИК: 1110 1000 0111 0111 0111 0011 1011 1100 1110 0011 0001 0000
КК: 1110100 1000101 0111010 0111010 0111010 0011101 1011000 1100010 1110100 0011101 0001011 0000000
Битовая скорость R равна:
,
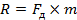где m – разрядность.
,
Кодовым расстоянием d для кода, содержащего m кодовых комбинаций, является минимальное расстояние между всеми парами кодовых комбинаций. Для кода Хэмминга d=3.
Кратность обнаруживаемой ошибки:
Кратность исправляемой ошибки:
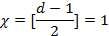
Декодирование и обнаружение/исправление ошибки.
Построим проверочную матрицу Хэмминга H=(
).
Введем ошибку во второй разряд комбинации 1110100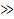 
1010100.
Перемножая столбец с разрядом комбинации, получим проверочную матрицу для комбинации:
Получим вектор S, путем сложения столбцов по модулю 2:
Ненулевой вектор показывает что есть ошибка. Находим такой столбец в проверочной матрице, его номер указывает на номер разряда в кодовой комбинации, в котором произошла ошибка, в данном случае – во втором. Изменяем значение второго бита и получаем 1110100, далее получаем проверочную матрицу для той комбинации:
Вектор S для нее:
,
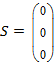что говорит о том, что ошибки нет и можно отбросить проверочные разряды.
Код Хэмминга, заданный как циклический код.
Используем код Хэмминга, заданный как циклический код с образующим полиномом G(x)=x3+x2+1.
Переведем исходные блоки в полиномиальный вид:
|
|
|
| Последовательность | Полином |
| 1110 | x3+x2+x |
| 1000 | x3 |
| 0111 | x2+x+1 |
| 0111 | x2+x+1 |
| 0111 | x2+x+1 |
| 0011 | x+1 |
| 1011 | x3+x+1 |
| 1100 | x3+x2 |
| 1110 | x3+x2+x |
| 0011 | x+1 |
| 0001 | 1 |
| 0000 | 0 |
Введем избыточность, умножая каждый полином на x3:
| Полином | Избыточный полином |
| x3+x2+x | x6+x5+x4 |
| x3 | x6 |
| x2+x+1 | x5+x4+x3 |
| x2+x+1 | x5+x4+x3 |
| x2+x+1 | x5+x4+x3 |
| x+1 | x4+x3 |
| x3+x+1 | x6+x4+x3 |
| x3+x2 | x6+x5 |
| x3+x2+x | x6+x5+x4 |
| x+1 | x4+x3 |
| 1 | x3 |
| 0 | 0 |
Деля избыточные полиномы на образующий полином, получаем кодовые полиномы:
| Избыточный полином | Кодированный полином | Кодовая комбинация |
| x6+x5+x4 | x6+x5+x4+x | 1110010 |
| x6 | x6+x2+x | 1000110 |
| x5+x4+x3 | x5+x4+x3+1 | 0111001 |
| x5+x4+x3 | x5+x4+x3+1 | 0111001 |
| x5+x4+x3 | x5+x4+x3+1 | 0111001 |
| x4+x3 | x4+x3+x | 0111001 |
| x6+x4+x3 | x6+x4+x3+x2 | 0011010 |
| x6+x5 | x6+x5+x2+1 | 1100101 |
| x6+x5+x4 | x6+x5+x4+x | 1110010 |
| x4+x3 | x4+x3+x | 0011010 |
| x3 | x3+x2+1 | 0001101 |
| 0 | 0 | 0000000 |
Битовая скорость R равна:
,
Кратность обнаруживаемой ошибки:
Кратность исправляемой ошибки:
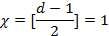
Декодирование и обнаружение/исправление ошибки.
Если при делении кодированного полинома на образующий полином, остаток от деления равен 0, то ошибок нет и служебную информацию можно отбросить.
Внесем ошибку в четвертый разряд полинома x6+x5+x4+x, т.е. добавим член x3 (1111010) и разделим результат на образующий полином, сдвигая кодовую комбинацию влево на разряд, до тех пор, пока остаток от деления не будет равен 1.
| Итерация | Делимое | Остаток |
| 1 | x6+x5+x4+x3 | x2+1 |
| 2 | x6+x5+x4+x2+1 | x2+x+1 |
| 3 | x6+x5+x3+x+1 | x+1 |
| 4 | x6+x4+x2+x+1 | x2+x |
| 5 | x5+x3+x2+x+1 | 1 |
Сдвигаем вектор 0000001 влево на 4 разряда, получаем 0001000, складываем этот вектор по модулю 2 с ошибочной кодовой комбинацией, получая в результате 1110010. Переводим комбинацию в полиномиальный вид, делим на образующий полином. Остаток от деления равен 0, значит проверочные разряды можно отбросить.
Кодирование с исправлением двойной ошибки.
В качестве кода, исправляющего ошибку двойной кратности, выберем сверточный код. Применим 3-х разрядный сверточный кодер с векторами связи g1=111 и g2=101.Ниже представлен граф переходов этого кодера.
|
|
|
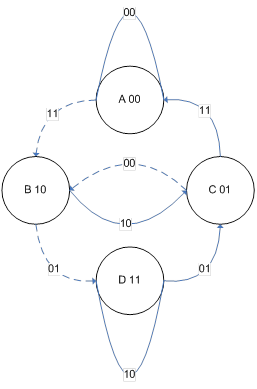
Переход по сплошной линии соответствует входному 0, по пунктирной – входной 1.Составим таблицу шифрования:
| Итерация | Входной символ | Состояние РС | Выходная посл. |
| 0 | - | 000 | - |
| 1 | 1 | 100 | 11 |
| 2 | 1 | 110 | 01 |
| 3 | 1 | 111 | 10 |
| 4 | 1 | 111 | 10 |
| 5 | 1 | 111 | 10 |
| 6 | 0 | 011 | 10 |
| 7 | 1 | 101 | 00 |
| 8 | 1 | 110 | 01 |
| 9 | 0 | 011 | 01 |
| 10 | 0 | 001 | 11 |
| 11 | 1 | 100 | 11 |
| 12 | 0 | 010 | 10 |
| 13 | 1 | 101 | 00 |
| 14 | 0 | 010 | 10 |
| 15 | 0 | 001 | 00 |
| 16 | 1 | 100 | 11 |
| 17 | 0 | 010 | 10 |
| 18 | 1 | 101 | 00 |
| 19 | 0 | 010 | 10 |
| 20 | 1 | 101 | 00 |
| 21 | 0 | 010 | 10 |
| 22 | 1 | 101 | 00 |
| 23 | 0 | 010 | 10 |
| 24 | 1 | 101 | 00 |
| 25 | 0 | 010 | 10 |
| 26 | 0 | 001 | 11 |
| 27 | 0 | 000 | 00 |
| 28 | 0 | 000 | 00 |
| 29 | 0 | 000 | 00 |
| 30 | 0 | 000 | 00 |
| 31 | 0 | 000 | 00 |
| 32 | 0 | 000 | 00 |
| 33 | 1 | 100 | 11 |
| 34 | 0 | 010 | 10 |
| 35 | 1 | 101 | 00 |
| 36 | 0 | 010 | 10 |
| 37 | 1 | 101 | 00 |
| 38 | 1 | 110 | 01 |
| 39 | 1 | 111 | 10 |
| 40 | 0 | 011 | 01 |
| 41 | 0 | 001 | 11 |
| 42 | 1 | 101 | 11 |
| 43 | 1 | 110 | 01 |
| 44 | 0 | 011 | 01 |
| 45 | 1 | 101 | 00 |
| 46 | 0 | 010 | 10 |
| 47 | 0 | 001 | 11 |
| 48 | 0 | 000 | 00 |
Построим по графу решетчатую диаграмму[1]:
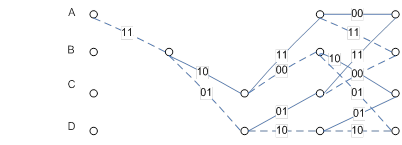
Битовая скорость R равна:
,
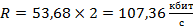Кратность обнаруживаемой ошибки:
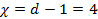
Кратность исправляемой ошибки:
,
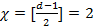где d – минимальное свободное расстояние, определяемое как метрика Хэмминга между двумя минимальными путями, сходящимися в одной точке (d=5).
Декодирование и исправление двукратной ошибки.
Для декодирования и исправления воспользуемся алгоритмом Витерби, согласно которому, необходимо посчитать метрики Хэмминга для всех путей в некоторый момент времени t и выбрать минимальную из них. Будем считать метрики Хэмминга для кодированной последовательности из 8 символов.
| Путь | Метрика Хэмминга для верной последовательности 11 01 10 10 | Метрика Хэмминга для ошибочной последовательности 10 01 11 10 |
| 11 10 11 00 | 4 | 4 |
| 11 01 01 11 | 3 | 3 |
| 11 10 11 11 | 4 | 4 |
| 11 01 01 00 | 3 | 3 |
| 11 10 00 10 | 3 | 5 |
| 11 01 10 01 | 2 | 4 |
| 11 10 00 01 | 5 | 7 |
| 11 01 10 10 | 0 | 2 |
Выбираем последнюю ячейку, так как она содержит минимальные метрики Хэмминга для обоих случаев. Ошибочную последовательность интерпретируем как путь, с которым у нее минимальная метрика Хэмминга. Для декодирования сообщения необходимо пройти по решетчатой диаграмме, интерпретируя блок кода как значение, при котором совершается переход, т.е. последовательность 11 01 10 10 декодируем в 1 1 1 1.
Импульсная модуляция
Представим сигнал кодировкой без возврата к нулю:
Достоинства метода:
— Простота реализации.
— Метод обладает хорошей распознаваемостью ошибок (благодаря наличию двух резко отличающихся потенциалов).
— Основная гармоника f0 имеет достаточно низкую частоту (равную N/2 Гц), что приводит к узкому спектру.
|
|
|
Недостатки метода:
— Метод не обладает свойством самосинхронизации. Даже при наличии высокоточного тактового генератора приёмник может ошибиться с выбором момента съёма данных, так как частоты двух генераторов никогда не бывают полностью идентичными. Поэтому при высоких скоростях обмена данными и длинных последовательностях единиц или нулей небольшое рассогласование тактовых частот может привести к ошибке в целый такт и, соответственно, считыванию некорректного значения бита.
— Вторым серьёзным недостатком метода, является наличие низкочастотной составляющей, которая приближается к постоянному сигналу при передаче длинных последовательностей единиц и нулей. Из-за этого многие линии связи, не обеспечивающие прямого гальванического соединения между приёмником и источником, этот вид кодирования не поддерживают. Поэтому в сетях код NRZ в основном используется в виде различных его модификаций, в которых устранены как плохая самосинхронизация кода, так и проблемы постоянной составляющей.
Представим сигнал кодировкой с возвратом к нулю:
Достоинства метода:
— Высокая помехоустойчивость по сравнению с кодом без возврата к нулю.
Недостатки метода:
— Более сложный процесс декодирования (на приемной стороне сигнал необходимо пропустить через дифференцирующую цепь для определения начала и конца импульса).
Представим сигнал манчестерским кодом:
Достоинства метода:
— Самосинхронизация.
Недостатки метода:
— Требует вдвое большей пропускной способности чем прямое кодирование.
Реализация импульсной модуляции в витой паре.
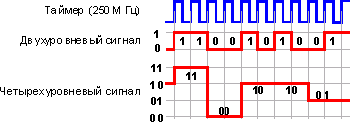
5-ти уровневая амплитудно-импульсная модуляция обеспечивает пропускную способность выше, чем бинарный сигнал, где каждый символ представлен одним битом (0 или 1). Так, каждый передаваемый символ представлен одним из 5ти разных уровней (-2, -1, 0, + 1, +2). Так как каждый символ может представляться 2-мя битами информации (4 уровня используется для представления 2х бит, плюс дополнительный пятый уровень используется для разработки метода поддержки коррекции ошибок (FEC)), скорость передачи данных вместе с пропускной способностью увеличивается. Распространенное четырехуровневое кодирование обрабатывает входящие биты парами. Всего существует 4 различных комбинации - 00, 01, 10, 11. Передатчик может каждой паре бит установить свой уровень напряжения передаваемого сигнал, что уменьшает в 2 раза частоту модуляции четырехуровневого сигнала, 125 МГц вместо 250 МГц, (рис.4), и следовательно частоту излучения. Пятый уровень добавлен для создания избыточности кода. В результате чего становится возможной коррекция ошибок на приеме. Это дает дополнительный резерв 6 дБ в соотношении сигнал/шум.
|
|
|
Реализация импульсной модуляции в коаксиальном кабеле.
Растущая потребность в повышении качества передачи изображения в системах охранного телевидения обусловила необходимость разработки полностью цифровых методов передачи видеосигнала. В этом случае для передачи двоичных символов в волоконнооптических системах связи обычно используется импульсно-кодовая модуляция; "0" соответствует отсутствию, "1" - наличию оптического излучения в волокне. Использование цифровых технологий обеспечило появление систем передачи одного или нескольких видеосигналов по одному оптическому кабелю с исключительно высоким качеством, не зависящим от длины линии связи.
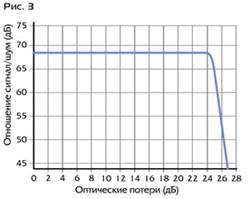
При этом в 2-3 раза удалось снизить искажения типа "дифференциальная фаза" и "дифференциальное усиление" по сравнению с аналоговыми методами. Использование даже 8битного кодирования позволяет создать транспортную среду, удовлетворяющую требованиям ГОСТ Р 5072594 и RS250C MediumHaul Transmission.
Например, цифровые кодеки серий "CFO" и "OPX" финской фирмы "Teleste" c 8битным кодированием обеспечивают отношение "сигнал/шум" не хуже 60 дБ при искажениях типа "дифференциальное усиление" - 1%, "дифференциальная фаза" - 1°. Переход к 12битному кодированию в последних разработках "Teleste" позволил создать многомодовую аппаратуру, обеспечивающую студийное качество передаваемых изображений в соответствии с CCIR601 и RS250C ShortHaul Transmission. Так, передатчики серии "CFO 121" обеспечивают в линии связи отношение "сигнал/шум" не хуже 70 дБ при искажениях типа "дифференциальное усиление" -1%, "дифференциальная фаза" - 1°.
Многоканальная передача.
Частотное уплотнение
|
|
|
Используются канальные сигналы, частотные спектры которых располагаются в неперекрывающихся частотных полосах. Формирование канальных сигналов осуществляется при помощи АМ, ЧМ или ФМ так, чтобы средние частоты спектров канальных сигналов соответствовали средним частотам отведенных полос каждого канала. В приемной части разделение каналов осуществляется набором частотных фильтров, каждый из которых пропускает спектр частот, принадлежащий только данному канальному сигналу. На рисунках показаны спектры сообщений, передаваемых по трем каналам и спектр сигнала, передаваемого по линии связи.
В многоканальных системах с временным разделением каналов (ВРК) канальные сигналы не перекрываются во времени, что обеспечивает их ортогональность.
Рассмотрим один из способов формирования канальных сигналов в системе с ВРК. Сообщения λk, поступающие от источников, подвергаются дискретизации по времени так, чтобы отсчеты одного сообщения не совпадали с отсчетами другого. В соответствии с моментами отсчетов вырабатываются импульсы, параметры которых меняются в зависимости от значений сообщений сообщения в каждом отсчете. Канальные сигналы, образованные из сообщения λ1, не совпадают по времени с канальными сигналами, образованными из сообщения λ2.
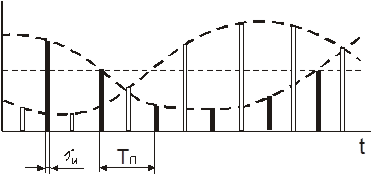
Множественный доступ
Для обеспечения возможности одновременного использования канала передачи данных несколькими пользователями применяют системы множественного доступа:
- множественный доступ с частотным разделением — при этом каждому пользователью предоставляется отдельный диапазон частот.
- множественный доступ с временным разделением — каждому пользователю предоставляется определенный временной интервал Таймслот, в течение которого он производит передачу и прием данных.
- множественный доступ с кодовым разделением — при этом каждому пользователю выдается кодовая последовательность, полученная, например, с помощью фунуции Уолша. Данные пользователя накладываются на кодовую последовательность таким образом, что передаваемые сигналы различных пользователей не мешают друг другу, хотя и передаются на одних и тех же частотах.
[1] Проведена селекция путей после такта t3 по алгоритму Витерби
|
|
|
