 |
В соответствии с ОСТ при малой скорости хода
|
|
|
|
,
, (6.10)
где
,
,
.
Вертикальная и килевая качки представляют собой поступательные вертикальные перемещения судна и вращательное по дифференту под действием сил 
, представляемых гармониками с амплитудами AFy, AMz, которые зависят от редукционных коэффициентов 
, 
.
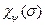Вертикальная качка:
(6.11)
Килевая качка:
(6.12)
В соответствии с ОСТ при малой скорости хода для вертикальной силы
,
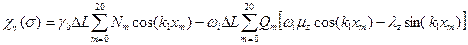где 
- абсцисса теоретического шпангоута,
; 
,
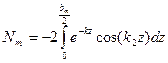-волновое число гармоники,
,
Интегралы вычисляются по контуру половины сечения 
-го теоретического шпангоута, который задается таблицей 
.
- уд. вес воды;
для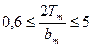 
, 
,
где
- ширина теретического шпангоута по расчетной ватерлинии,
- осадка теоретического шпангоута, 
- присоединенные массы и коэффициенты демпфирования по каждому из шпангоутов;
для 
, 
,
где 
, 
- площадь погруженной части теоретического шпангоута.
Для момента относительно оси oz
(6.13) Рыскание судна по курсу представляет собой вращательное движение относительно оси oy, которое обусловлено воздействием силы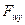 
, гармоникой с амплитудой AMу 
, зависящих в соответствии с (34) от 
, (6.14)
где 
.
Результаты расчета редукционных коэффициентов поперечной качки и рыскания для рассматриваемого судна и для 
приведены на рис.6.4
Рис.6.4
Тема 5.4. Расчет спектров кинематических параметров ОМТ на волнении.-2 час. Частотные характеристики, связывающие входные силы и моменты волнения с кинематическими параметрами движения ОМТ. Применение теоремы Хинчина для расчета спектров и статистических характеристик кинематических параметров.
Нерегулярное волнение
Нерегулярность и хаотичность взволнованной поверхности позволяют рассматривать волнение как случайный процесс, при котором амплитуды и частоты гармоник изменяются случайным образом. Такое волнение называется нерегулярным. В этом случае волновая ордината 
представляется как случайная стационарная функция, удовлетворяющая условиям эргодичности. Эта функция является центрированной, мерой интенсивности служит дисперсия 
, спектр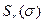 
и плотность распределения высоты волны 
.
|
|
|
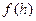Кроме того, для оценки интенсивности используется понятие высоты волны 3-% обеспеченности. Под этим понимают такую высоту волны, вероятность превышения которой составляет 3%, т.е. 
. Между и 
существует зависимость, которая определяется плотностью распределения высот волн. Практикой установлено, что плотность распределения амплитуд волн подчиняется закону Релея
. (6.15)
Вероятность, что высота волны не превысит значения 
,
тогда 
,
откуда после логарифмирования можно получить
; 
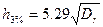. (6.16)
Связь с балльностью волнения представлена в табл.6.1
Табл.6.1
| Волнение, баллы | |||||||||
| , м
| 0-0.25 | 0.25-0.75 | 0.75-1.25 | 2.25-2.0 | 2.0-3.5 | 3.5-6.0 | 6.0-8.5 | 8.5-11 | Более 11 |
Корреляционные функции. С помощью волнографов в течение длительного промежутка времени записывается высота волны 
в заданной точке определенной акватории.
Используя гипотезу об эргодичности случайного процесса с помощью корреляторов рассчитывается корреляционная функция волновой ординаты
. (6.17)
Спектральные характеристики получаются с помощью преобразования Фурье
(6.18)
и обратно
, (6.19)
причем
. (6.20)
Рассмотренная упрощенная модель получается в предположении двумерного волнения, при котором гребни волн имеют бесконечную длину и перемещаются в одном направлении, сохраняя параллельность. Более точной является модель трехмерного волнения, которая образуется суперпозицией большого числа двумерных волн с разными направлениями распространения. Спектр двумерного волнения представляет собой функцию одного аргумента-частоты .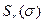
|
|
|
Пример. Пусть 
, тогда
.
Если на вход системы с передаточной функцией 
поступает случайный процесс спектральная плотность которого 
, то спектральная плотность сигнала на выходе системы 
определяется в соответствии с теоремой Хинчина
Спектр трехмерного волнения зависит как от частоты, так и угла 
между главным направлением распространения волн и направлением, в котором определяется спектральная плотность. Между этими спектрами существует связь:
при соблюдении условия сохранения энергии
,
позволяющая свести расчеты движения судна на трехмерном волнении к расчетам на двумерном.
|
|
|
