Расчетные спектры морского волнения.

Известны спектры Ньюмена, Бретшнайдера, Пирсона-Московица, Вознесенского, …

В настоящее время для описания спектров используются экспоненциальные и дробно-рациональные спектры.

Стандартный экспоненциальный спектр, рекомендованный ОСТ 5.1003-80 имеет вид

где , (6.21)

, (6.22)

-дисперсия волновых ординат, частота максимума спектра и средняя частота, соответствующие спектральным плотностям .

Параметры спектров определяются по формулам:

,

(6.23)

где ,

- высота волны 3% обеспеченности (определяется балльностью волнения, см.табл.).

, ,

, , ,

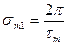где , см. ОСТ 5.1003-80.и рис.6.5

 

Рис.6.5

Среди дробно-рациональных спектров широко используется спектр вида

, (6.24)

которому соответствует корреляционная функция

.

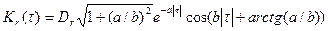Для развитого морского волнения соблюдается:

- , тогда ;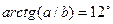

-частоты максимумов спектров однозначно связаны с () и практически равны .

-дисперсия волновой ординаты .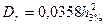

Так для 5-ти балльного волнения [15]

и , , 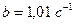. Тогда в соответствии с (2.25)

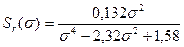
В расчетах также используется спектр угла волнового склона , который связан со спектром волновых ординат 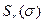соотношением

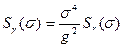. (6.25)

 

Примеры расчета спектра волновых ординат

Для волнения 5 баллов в соответствии с табл. и рис.

=3.5 м., =7 сек.

Тогда =0.89714, 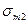=0.6279, =0.73565, =5.39, =1.16512,

=0.1253, =0.1109, 0.0144.

Значимые значения спектра находятся в диапазоне частот от 0.4 до 2.4 с^-1.

График спектра приведен на рис. 6.6

Рис.6.6

 

Спектр угла волнового склона приведен на рис.6.7

Рис.6.7

Для волнения 10 баллов

=11 м., =13.5 сек.

Тогда =0.46518, 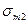=0.3256, =0.38144, =10395, =0.60413,

=4.3318, =3.83364, 0.49815.

Значимые значения спектра находятся в диапазоне частот от 0.2 до 1.4 с^-1.

График спектра приведен на рис. 6.8

Рис.6.8

Спектр угла волнового склона приведен на рис.6.9

Рис. 6.9

При моделировании силовых воздействий используется представление сил и моментов вида. Для определения амплитуд гармоник A_Fxi,A_Fyi, A_Fzi, A_Mxi, A_Myi, A_Mzi спектр волновых ординат или угла волнового склона разбивается на сумму прямоугольников с площадями или , привязанных к некоторой частоте 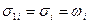. Сумма всех площадей определяет дисперсию соответствующего процесса. Вычисляются корни квадратные из полученных площадей. Тогда случайная функция волновых ординат имеет вид

,

аналогично случайная функция угла волнового склона

.

Значения ординат для соответствующих приведены в табл. 6.2

Табл. 6.2 (5 баллов)

	0.4	0.5	0.6	0.7	0.8	0.9	1.0	1.1	1.2
	1.45Е-3	2.15Е-2	3.98Е-2	0.0587	0.0776	0.0882	0.0764	0.0666	0.0564
	1.3	1.4	1.5	1.6	1.7	1.8	1.9	2.0	2.1
	0.0472	0.0394	0.0333	0.0278	0.0235	0.0200	0.0172	0.0148	0.0129
	2.2	2.3	2.4
	0.0113	0.0099	0.0087

 

Табл. 6.3 (10 баллов)

	0.2	0.26	0.32	0.38	0.44	0.5	0.56	0.62	0.68
	4.11Е-3		3.6601	11.5511	15.7101	15.5131	13.6001	11.3012	9.1900
	0.74	0.8	0.86	0.92	0.98	1.04	1.1	1.16	1.22
	7.4721	6.1094	5.0211	4.1600	3.4805	2.9402	2.5021	2.1408	1.8501
	1.28	1.34
	1.611	1.4100

 

Для угла волнового склона в Табл.6.4,6.5 соответственно.

 

Табл.6.4 (5 баллов)

	0.4	0.5	0.6	0.7	0.8	0.9	1.0	1.1	1.2
	2.37Е-5	5.47Е-4	1.46Е-3	2.93Е-3	5.07Е-3	6.79Е-3	7.78Е-3	8.21Е-3	8.27Е-3
	1.3	1.4	1.5	1.6	1.7	1.8	1.9	2.0	2.1
	8.13Е-3	7.87Е-3	7.57Е-3	7.25Е-3	6.93Е-3	6.62Е-3	6.33Е-3	6.05Е-3	5.79Е-3
	2.2	2.3	2.4
	5.55Е-3	5.33У-3	5.12Е-3

 

 

Табл. 6.5 (10 баллов)

	0.2	0.26	0.32	0.38	0.44	0.5	0.56	0.62	0.68
	1.67Е-5	1.13Е-3	0.0382	0.0169	0.309	0.396	0.434	0.441	0.433
	0.74	0.8	0.86	0.92	0.98	1.04	1.1	1.16	1.22
	0.417	0.398	0.378	0.359	0.341	0.324	0.308	0.293	0.281
	1.28	1.34
	0.268	0.256

 

 

Тогда амплитуды i- х гармоник силовых воздействий определяются соотношениями:

где , , , , , - редукционные коэффициенты, вычисленные для соответствующих частот.

 

Алгоритмы расчета спектров процессов ОМТ на волнении.

Рассмотрим процесс рыскания корабля на волнении.

Управляемое движение корабля на волнении описывается уравнениями

 

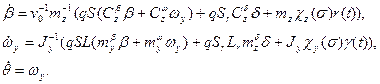(6.26)

Возможны два подхода:

1-й заключается в следующем

- для заданной балльности, скорости хода и угла определяется набор истинных частот и соответствующих им кажущихся , для вычисляются редукционные коэффициенты, которые домножаются на выбранные случайные амплитуды спектров пересчитанных к кажущимся частотам. Моделируется приведенная система уравнений. Для исследуемого процесса вычисляется дисперсия по одной длинной реализации на основании соотношения

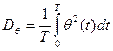при .

2-й способ связан с аналитическим вычислением спектра и дисперсии . Для этого

необходимо по исходным уравнениям вычислить передаточные функции в соответствии с рис.6.10

 

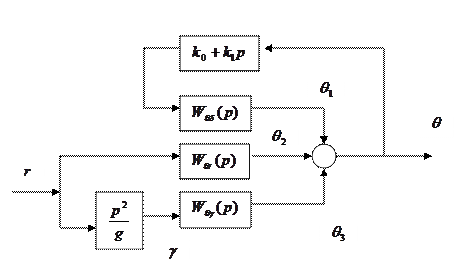
Рис.6.10

 

Путем несложных преобразований схема может быть приведена к виду, рис.6.11

 

Рис.6.11

где .

Тогда спектр выходного сигнала определяется по формуле

.

 

 

Силы волнового дрейфа.

Рассмотренные ранее силы имели нулевую постоянную составляющую. Однако в соответствии с исходными данными отмечается наличие в горизонтальной плоскости постоянных сил и момента волнового дрейфа. Силы и момент волнового дрейфа, действующие на маневрирующее судно в условиях двумерного нерегулярного волнения заданного спектра 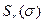, определяется выражениями

(6.27)

где ,

,

 

Для принятого ранее спектра ординат морского волнения, величина принимает следующие значения:

- для пяти баллов =0.017018;

- для десяти баллов =36,340032.

6.7Силовые воздействия ветра (аэродинамические силы) подвержены существенным изменениям из- за больших отклонений от средней скорости, вызываемых порывами и шквалами. Порывы, являющиеся следствием турбулентности потока воздуха у поверхности воды, представляют блоьшую опасность, так как они накладываются на сильный штормовой ветер. Изменение скорости достигает 100% от среднего значения.

В табл.6.6 приведены значения средних скоростей ветра и шквальных для различных балльностей ветра по шкале Бофорта на высоте 6 м от поверхности моря. Здесь же приведены значения давлений для средних скоростей и аэродинамические лобовая и боковая силы действующие на судно при средней и шквальной скорости ветра ( =300 м², =1160 м²).

Табл.6.6

Сила ветра балл	Скорость ветра и аэродинамические силы	Удельное давление р Па
Средняя М/c	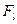, кгс	,кгс	Шквальная М/c	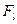,кгс	,кгс	Средняя	Шквальная
	0-0,5			1,0	18.75	72.5		0.125
	0,6-1,7	27.0	104.4	3,2	192.0	742.4	0.18	1.28
	1,8-3	91.5	383.38	6,2	720.2	2786.9	0.661	4.805
	3-5							12.5
	5-8	792.15					5.281	40.5
	8-11	1518.75					10.125	60.5
	11-14	2929.5	11327.4				19.531	112.5
	14-17						30.031
	17-20						42.781	220.5
	20-24						60.5	300.125
	24-28						84.5
	28-32						112.5
	32-36						144.5

 

 

Поскольку процесс волнообразования тесно связан с передачей энергии от ветра к волнам, то следует увязывать балльность волнения (и соответствующие расчеты качек) с балльностью ветра по шкале Бофорта, см. Табл.6.7

 

Табл.6.7

Балльность ветра
Балльность волнен.

 

 

Скорость ветра меняется также по высоте (судна)

, ,

эффективная скорость ветра определяется по формуле [4]

(6.28)

 

где v - дополнительная скорость ветра при порыве.

Аэродинамическая сила давления ветра на надводную часть корпуса и надстройки 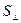определяется по формуле

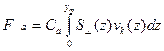, (6.29)

где 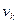- кажущаяся скорость ветра, действующая на судно с учетом его перемещения, -обобщенный аэродинамический коэффициент.

В данном случае используются соотношения

используются соотношения

, ,

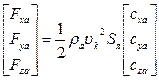для их определения необходимо знать соотношения для аэродинамических коэффициентов объекта .

Приведем примеры зависимости коэффициентов аэродинамических сил от

,

 

.

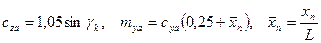Входящие в формулы значения площади лобовой и боковой парусности, а также абсцисса центра парусности судна пр.20 составляют, например

Скорость и угол кажущегося горизонтального ветра определяются соотношениями

 

При шквале дополнительная скорость ветра v_а изменяется от среднего значения до максимального (вдвое превышающее среднее значение) по линейному закону, причем время нарастания зависит от максимального значения дополнительной скорости в соответствии с таблицей 6.8.

 

 

Табл.6.8

va м/c
c

 

Волновая составляющая скорости ветра определяется морским волнением. Ее корреляционная функция и спектральная плотность совпадают с аналогичными характеристиками для функции волновой ординаты, но со значительно меньшей дисперсией, в следствии чего волновой составляющей скорости ветра пренебрегают.

 

 

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: