 |
Защита от ошибок. Помехоустойчивое (канальное) кодирование
|
|
|
|
4.1 Определение оптимальных параметров помехоустойчивого кодирования
Необходимо отметить, существует два основных метода защиты от ошибок передаваемых сигналов: 1 - обнаружение ошибок и повторная передача ошибочной последовательности, 2 – обнаружение ошибок и их исправление в приемном устройстве. Примем, что в рассматриваемой СПДИ применяется первый метод защиты от ошибок, при котором для проверки наличия ошибок используется контрольный бит четности (дополнительный бит, присоединяемый к данным). При этом приемное устройство не предпринимает попыток исправить обнаруженную ошибку, оно просто посылает запрос на повторную передачу данных. Для осуществления такого исправления ошибок рассматриваемая СПДИ имеет канал переспроса и в целом является полудуплексной системой, т.е. передача полезной информации от М источников производится только в одном направлении, в обратном же направлении передаются автоматические запросы на повторную передачу ошибочных сообщений. Причем передающее устройство перед началом очередной передачи ожидает подтверждения об успешном приеме.
Помехоустойчивое (или канальное) кодирование представляет собой класс преобразований канального видеосигнала для повышения качества связи, в результате которых информационный сигнал становится менее уязвимым к помехам. Существует условно два способа канального кодирования: кодирование самого сигнала, (когда в передающей части СПДИ производятся ряд процессов над формой передаваемого сигнала), и метод структурированных последовательностей (когда в цифровой сигнал вводится по определенному закону информационная избыточность, которая и служит для определения ошибок на приемной стороне).
|
|
|
Рассмотрим только второй способ канального кодирования, который нашел применение в исследуемой СПДИ. Заметим, что помехоустойчивое кодирование делится на три подкатегории помехоустойчивых кодов: блочные, сверточные и турбокоды.
В нашем случае для сравнения характеристик помехоустойчивого кодирования рассмотрим варианты блочного линейного корректирующего кодирования кодами Хэмминга.
При использовании блочных кодов исходные данные делятся на блоки (слова) Кс из к бит, которые называют битами сообщения. В нашем случае длина слова Кс=10 бит. В процессе помехоустойчивого кодирования каждый Кс блок данных преобразуется в больший блок из n бит, который называется кодовым словом, или канальным символом Кк. К каждому слову кодирующее устройство прибавляет r = (n - k) проверочных бит, которые также называются избыточными битами, или битами четности, и новой информации не несут.
Необходимо, исходя из разницы между пропускной способностью аналогового канала связи Ск и информационной производительностью СПДИ Ic, определить все необходимые числовые значения параметров заданного помехоустойчивого кода и выбрать наиболее оптимальные из них. Для этого воспользуемся методикой расчета параметров кода Хэмминга, приведенной в источнике [7].
Коды Хэмминга – это простой класс блочных кодов, которые имеют следующую структуру:
(4.1)
где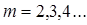 
- основание блочного кода.
Рассмотрим случаи, когда основание кода m =2,3,4…, и определим оптимальные параметры кода.
Из формулы (4.1) вычислим: значения n и к. Где n – число бит кодового слова; к - число информационных бит.
Тогда число проверочных бит кода:
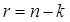(4.2)
Избыточность кода составит:
(4.3)
Степень кодирования информации, показывающая долю кода, приходящуюся на полезную информацию:
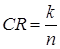(4.4)
т.е. каждый кодовый бит несет k / n бит информации.
|
|
|
Минимальное расстояние кодов Хэмминга dmin равно 3, поэтому, способность кода к исправлению ошибок t и возможность определения наличия ошибки e будут определяться соответствующими выражениями:
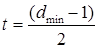(4.5)
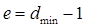(4.6)
Так как 
, то эти коды способны исправлять все однобитовые ошибки, или определять все модели ошибки из двух или меньшего числа ошибок в блоке (слове), т.к. 
.
Вероятность появления битовой ошибки при кодировании кодами Хэмминга Р b кх в нашем случае можно записать в следующем виде:
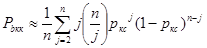(4.7)
где j - кратность ошибки, а именно количество неверно принятых символов в блоке (слове); ркс – вероятность ошибочного приема канального символа (кодового слова) Кк. В частности, для кодов Хэмминга вместо уравнения (4.7) можно использовать другое эквивалентное уравнение:
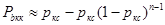(4.8)
Для описания гауссовского канала с использованием когерентной бинарной фазовой манипуляции, вероятность ошибочного приема канального символа (кодового слова) можно выразить через соотношение:
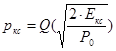(4.9)
Здесь Q () – Гауссов интеграл ошибок, значения которого приведены в [3,стр.1060];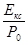 
- отношение энергии кодового символа к спектральной плотности мощности помехи. Чтобы связать 
с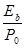 
- отношение энергии одного бита сигнала к спектральной плотности мощности помехи на входе приемника, используем следующее выражение:
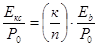(4.10)
Для кодов Хэмминга уравнение (4.10) примет вид:
(4.11)
Среднее время безошибочной работы в одном телеметрическом канале (канале источника сообщения) Θбр i (без учета помехоустойчивого кодирования) определяется выражением:
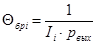(4.12)
где 
- битовая вероятность появления ошибки на выходе декодера (без учета помехоустойчивого кодирования), выражение для нахождения численного значения которой будет рассмотрено ниже, 
- производительность источника информации.
Среднее время безошибочной работы в групповом канале передачи данных Θбр (без учета помехоустойчивого кодирования) определяется выражением:
(4.13)
где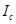 
- производительность СПДИ информации.
Таким образом, согласно вышеизложенной методики, рассчитаем параметры помехоустойчивого кодирования при различных значениях основания кода m.
|
|
|
Для m =2:
;
;
;
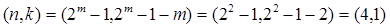
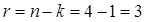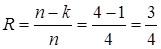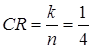Согласно формулы (4.11) получим:
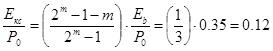
при значении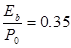 
(рассчитанном в п.8.1).
Тогда
из [3,стр.1060]
Для m = 3:
;
;
;
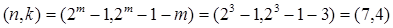
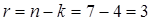, где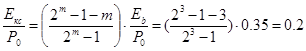 
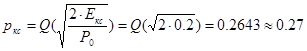
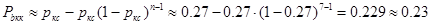
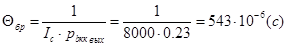
Для m =4:
; 
; 
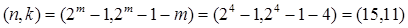
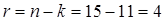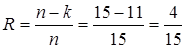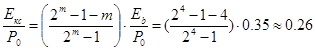
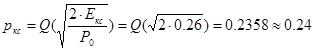
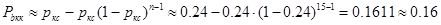
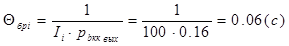
Как показали расчеты вероятность появления битовой ошибки при кодировании кодами Хэмминга Р b кх тем меньше, чем больше основание кода m, т.е.чембольшее количество проверочных символов вводится в информационный сигнал.
Рассчитаем, оптимальные параметры кода Хэмминга (с точки зрения обеспечения СПДИ наименьшей вероятностью Р b кх). С этой целью рассчитаем количество контрольных бит r, которое можно ввести в систему, исходя из того, что при расчетах пропускной способности канала связи (КТЧ) и информационной производительности СПДИ было получено соотношение 
или иначе
(4.14)
Как было рассчитано ранее в (3.9):
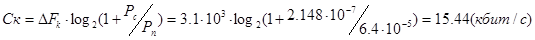
Подставим в предыдущее выражение вместо Ск значение ∆Ск
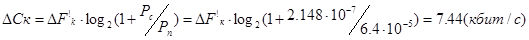
Выразим и рассчитаем
-
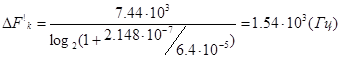эквивалентную ширину полосы пропускания.
Используя последнюю формулу, выразим r! – количество бит четности, которые можно ввести в кодовое слово в передаваемом сигнале (исходя из условия, что пропускная способность канала ТЧ – главный сдерживающий фактор увеличения возможного числа проверочных бит и как следствие этому - повышения помехоустойчивости системы):
.
где T б – длина одного тактового импульса.
Таким образом, в заданных условиях функционирования СПДИ, оптимальным количеством проверочных битов на каждый блок исходного сообщения кода Хэмминга, при котором вероятность появления битовой ошибки Pb кх будет минимальной 
, а среднее время безошибочной работы М-го канала телеметрии будет максимальным 
станет равным r ! = r =5. В связи с этим, так как по условию к=10 (бит), то n = k + r =15 (бит). Код Хэмминга в этом случае будет иметь вид, показанный для m=4, а именно 
, причем 1 бит из k бит кодового слова имеет смысл маркера кадра системы синхронизации, которая будет рассмотрена ниже.
Помехоустойчивое кодирование кодами Хэмминга, как показали расчеты, приводит к необходимости решения компромисса в СПДИ: кодирование с коррекцией ошибок требует избыточности, следовательно, увеличения скорости передачи информации и конечно увеличения полосы пропускания системы. Иными словами, в нашем случае, при кодировании кодом Хэмминга с параметрами (15,11) помехоустойчивость СПДИ увеличилась в 1.25 раза, т.е.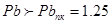 
, производительность СПДИ Ic увеличилась примерно в 1.93 раза и стала сопоставима с пропускной способностью канала ТЧ, т.е. 
.
|
|
|
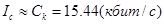Схема кодера, удовлетворяющего условию (15,11) приведена на рис.4.1
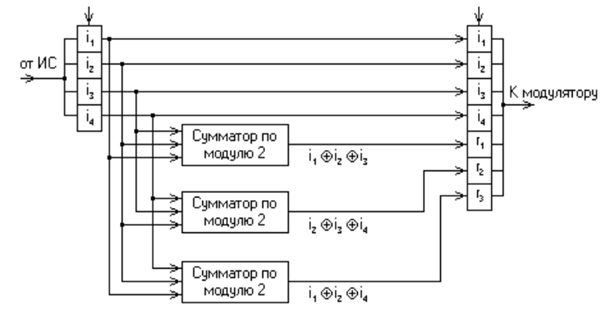
Рис.4.1 Схема кодера, удовлетворяющего условию (15,11).
Схема декодера, удовлетворяющего условию (15,11) приведена на рис.4.2
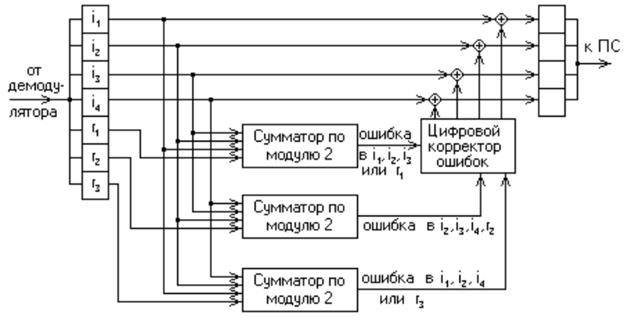
Рис.4.2 Схема декодера, удовлетворяющего условию (15,11).
|
|
|
