 |
Исследование простейших линейных цепей
|
|
|
|
СИНУСОИДАЛЬНОГО ТОКА
Цель работы
Экспериментальное исследование амплитудных и фазовых соотношений между токами и напряжениями в цепях RL, RC, RLC.
Подготовка к работе
1. Изучить рассматриваемую тему по конспекту лекций и одному из учебников [1–3].
2. Для цепи рис. 3.1 рассчитать комплексы действующих значений тока и напряжений на резисторе и емкости. Исходные данные для расчетов взять из табл. 3.1.
На всех рабочих местах емкость С = 6000 пФ, действующее значение напряжения источника U = 4 В. Начальную фазу источника входного напряжения принять равной нулю.
Заполнить табл. 3.2. Построить на комплексной плоскости вектор тока и потенциальную диаграмму напряжений.
 |
Рис. 3.1
Таблица 3.1
| Номер бригады | ||||||||
| f, кГц | ||||||||
| R, Ом | ||||||||
| L, мГн | 3,95 | 5,24 | 6,08 | 4,05 | 9,18 | 7,99 | 3,85 | 7,23 |
Таблица 3.2
| Величина | U1, B | UR, B | UC, B | φ, град. | I, A | Z ВХ=zejφ |
| Расчет | ||||||
| Эксперимент |
3. На рис. 3.1 заменить емкость индуктивностью. Выполнить расчеты, аналогичные п. 2; результаты расчетов занести в табл. 3.3.
Таблица 3.3
| Величина | U1, B | UR, B | UL, B | φ, град. | I, A | Z ВХ=zejφ |
| Расчет | ||||||
| Эксперимент |
4. Для цепи на рис. 3.2 выполнить расчеты, аналогичные п. 2. Результаты занести в табл. 3.4. Построить на комплексной плоскости вектор тока и потенциальную диаграмму напряжений.
Рис. 3.2
Таблица 3.4
| Величина | U1, B | UR, B | UL,B | UС,B | φ, град. | I, A | Z ВХ=zejφ |
| Расчет | |||||||
| Эксперимент |
|
|
|
5. Подготовить бланк отчета.
6. Ознакомиться с описанием установки.
7. Подготовить ответы на контрольные вопросы.
Описание установки
Генератор синусоидального напряжения, электронные вольтметры V1 и V2 и фазометр работают от сети переменного напряжения. Их зажимы «Земля» должны быть соединены между собой. В связи с этим вольтметрами V1 и V2 можно измерять напряжение между любой точкой цепи и общей точкой соединения всех перечисленных выше приборов. Вольтметр V3 не связан с сетью переменного напряжения. Им можно измерять напряжение между любыми точками исследуемой электрической цепи. Фазометр показывает разность между фазами напряжений, подаваемых на зажимы «Сигнал» и «Опора». Величину тока определяют косвенным способом, посредством измерения напряжения на известном сопротивлении резистора R.
Выполнение работы
1. Исследование режима в цепи RC. Собрать цепь по схеме рис. 3.1. Установить частоту и напряжение согласно заданию. Записать в табл. 3.2 показания приборов. Экспериментальную величину Z ВХ рассчитывают на основании показаний приборов. Сравнить результаты эксперимента с расчетными. Убедиться, что напряжение источника равно геометрической сумме напряжений на емкости и резисторе.
2. Исследование режима в цепи RL. Заменить конденсатор (схема на рис. 3.1) катушкой индуктивности. Выполнить измерения и расчеты, аналогичные для цепи RC, их результаты занести в табл. 3.3.
3. Исследование режима в цепи RLC. Собрать цепь по схеме рис. 3.2. Записать в табл. 3.3 показания приборов и расчетов, выполненных на основе этих показаний. Изменяя частоту источника, добиться изменения характера входного сопротивления, наблюдая за показаниями фазометра.
Контрольные вопросы
1. Как связаны между собой мгновенные значения токов и напряжений на элементах R, L, C?
2. Записать выражения для комплексного сопротивления индуктивности и емкости.
|
|
|
3. Дать полное название следующим величинам: 
z, Z, R, X.
4. Записать выражения для перехода от показательной формы записи комплексного сопротивления Z к алгебраической, также для обратного перехода от алгебраической формы к показательной.
5. Построить качественно векторную и потенциальную диаграммы для схемы, заданной преподавателем.
Теоретические сведения
1. При анализе установившихся режимов синусоидального тока в линейных электрических цепях применяют символический метод расчета, основанный на изображении синусоидальных функций времени комплексными числами: комплексами действующего или комплексами амплитудного значения.
Если мгновенное значение э.д.с.
e (t) = Em sin (ωt + ψ),
то комплекс амплитудного значения (или комплексная амплитуда)
,
комплекс действующего значения
.
Аналогично записываются комплексные значения и для токов.
Комплексные сопротивления Z отдельных элементов сведены в табл. 3.5.
Таблица 3.5
| Элементы цепи | Комплексное сопротивление Z = R + jX |
| R | Z R = R |
| L | Z L = jωL |
| C | 
|
Расчет установившихся процессов синусоидального тока проводится всеми известными методами, но все уравнения составляются относительно комплексов амплитудного или комплексов действующего значения. Этот метод называется символическим методом расчета.
2. Порядок расчета цепи символическим методом:
1 – от синусоидальных функций времени (э.д.с., тока, напряжения) перейти к соответствующим комплексам действующего (или амплитудного) значения;
2 – определить комплексные сопротивления пассивных элементов схемы;
3 – в зависимости от сложности заданной схемы рассчитать искомую комплексную величину рациональным методом;
4 – по полученным комплексам действующего (или амплитудного) значения записать мгновенное значение искомых величин по соотношению 
(аналогично для тока).
3. Форма записи комплексных чисел.
Любое комплексное число может быть изображено точкой на комплексной плоскости (рис. 3.3). Положение этой точки однозначно определяется парой чисел а и b или М и φ. В соответствии с этим существуют две формы записи комплексных чисел: алгебраическая и показательная.
|
|
|
Рис. 3.3
1 – алгебраическая А = а + jb, где а – действительная часть комплексного числа, b – мнимая часть комплексного числа.
2 – показательная 
, где М – модуль комплексного числа, φ – аргумент комплексного числа.
Переход от одной формы записи комплексного числа к другой выполняется в соответствии с формулами тригонометрии. Все вычисления на калькуляторе желательно сопровождать вспомогательными построениями.
На рис. 3.4 показаны а, b, М, φпри расположении комплексного числа в различных четвертях комплексной плоскости.
a б в г
Рис. 3.4
Примечание: аргумент комплексного числа φ всегда отсчитывается от положительного направления оси действительных чисел.
Если отсчет ведется против часовой стрелки (как показано на рис. 3.4), то угол φ записывается со знаком «плюс», если по часовой стрелке, то угол φ записывается со знаком «минус».
Например, на рис. 3.4, г число А может быть записано 
.
Пример 1. По заданным а и b определить М и φ:
.
Отмечаем на комплексной плоскости заданное комплексное число А (рис. 3.5). Из рисунка видно, что
, φ = 180°– 77,5º= 102,5º,
.
Следовательно,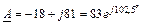 
.
Рис. 3.5
Пример 2. По заданным М и φ определить а и b:
.
Изобразим на комплексной плоскости заданное комплексное число без масштаба (рис. 3.6). Как видно из чертежа, угол a прямоугольного
треугольника со сторонами а, b и М
равен a = 210º – 180º = 30º.
Тогда │ а │= M cos a= 15 cos 30º= 13,
│ b │= M sin a= 15 sin 30º= 7,5.
Следовательно, 
.
Рис. 3.6
Сложение и вычитание комплексных чисел удобно производить в алгебраической форме, а умножение и деление – в показательной. При необходимости избавиться в выражении от комплексного числа в знаменателе можно домножить и числитель, и знаменатель на комплексно-сопряженное ему число, т.е.
.
4. Векторная диаграмма токов и топографическая диаграмма напряжений.
Совокупность векторов токов и потенциалов на комплексной плоскости с указанием векторов напряжений на всех элементах называется векторной диаграммой токов и топографической диаграммой напряжений.
|
|
|
Качественное построение векторной диаграммы токов и топографической диаграммы напряжений можно провести для цепи, содержащей только один источник энергии и последовательно-параллельное соединение пассивных элементов. Построение проводится в том же порядке, в котором ведется расчет методом пропорциональных величин, т.е. начинать качественное построение нужно, произвольно задавшись током в наиболее удаленной от источника и наиболее нагруженной ветви.
ЛАБОРАТОРНАЯ РАБОТА № 4
|
|
|
