Пример расчета фильтра нижних частот на заданные параметры

 

Аналитический метод расчета цепочных фильтров основан на нахождении оптимальных параметров фильтра по заданной характеристике собственного или рабочего затухания. При этом реализуется фильтр, удовлетворяющий заданным условиям, при минимальном числе элементов, что гарантирует минимальное искажение в полосе пропускания. Отметим, что, так как последовательно и параллельно-производные звенья фильтров являются дуальными, т.е. взаимообратными, а свойства таких схем в отношении передачи энергии аналогичны, то количество расчетных формул, используемых для расчета фильтров, будет вдвое уменьшено. Поэтому ведется единый расчет фильтра.

Требуется рассчитать фильтр, удовлетворяющий следующим техническим требованиям:

1. Полоса пропускания

= 50 кГц, = 100 кГц,

где  и  соответственно нижняя и верхняя граничные полосы пропускания.

2. Полоса задерживания

От = 115 кГц и выше

где  и  соответственно верхняя и нижняя граничные полосы задерживания.

3. Рабочее затухание в полосе пропускания

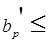 7дБ = =0,805 неп

4. Рабочее затухание в полосе задерживания

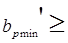 50 дБ = =5,75 неп

5.Фильтр включается между сопротивлением нагрузок

= 1000 Ом

6.Отклонение характеристического сопротивления от номинального в полосе пропускания (коэффициент несогласованности)

 = 10 % =0,1

7. Амплитуда входного сигнала

 = 5 В

9. Коэффициент использования полосы пропускания.

8. Рекомендуется выполнить катушки индуктивностей на альсиферовых сердечниках.

Прежде чем приступить к расчету фильтра, необходимо определить критерий полосности

 

=

 

Так как n < 2, рассчитываем фильтр как полосовой.

Зная вычислим ,затем определим затухание несогласованности

Выбрав класс фильтра по сопротивлению (обычно 2-ой), т.е. =2, найти параметр

 

 

Далее определить расчетный параметр полосы пропускания

 

 

и затем расчетный параметр

 

 

Найдем коэффициент использования полосы пропускания

 

И только потом можно определить коэффициент использования полосы задерживания  и теоретическую частоту среза. Для реальных фильтров 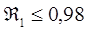. Заданные параметры  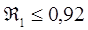и = 100 кГц, определим теоретическую частоту среза

 

 

Так как теоретическая частота среза лежит в пределах переходной области, она удовлетворяет предъявленным условиям. Исходя из этого, определяем предварительный коэффициент использования полосы пропускания

 

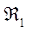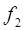Поскольку величина не превышает предельно достижимого в реальных фильтрах значения 0,98, останавливаемся на этих значениях и . Определяем коэффициент использования полосы задерживания  и расчетные параметры 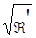- расчетный параметр и - расчетный параметр полосы задерживания:

 

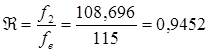
Зная , определяем затухание одного звена фильтра с учетом потерь в полосе задерживания

 

 

Далее находим минимальное собственное затухание всего фильтра в полосе задерживания, которое необходимо для обеспечения гарантируемого минимума затухания

 

 

По найденным значениям  и  определяем число звеньев N (или, что то же самое, класс фильтра по затуханию)

 

 

 

Для выбранного округленного числа звеньев N=4 пересчитываем величины , , , а также 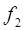. Уточнив все эти параметры проверяем отклонение характеристического сопротивления от номинального.

 

 

 

Зная 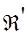, пересчитываем коэффициент использования полосы задерживания

 

,

 

используя который, определяем уточненную верхнюю теоретическую частоту среза

 

 

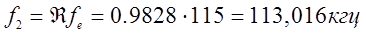
Полученное значение теоретической частоты среза удовлетворяет исходным требованиям, так как находится в переходной области. Далее определяем уточненный коэффициент использования полосы пропускания

 

,

Теперь по сути дела возвращаемся в начало расчета. Для проверки отклонения характеристического сопротивления фильтра от номинального сопротивления нагрузки в полосе пропускания рассчитываем параметры ,  и (по данным полосы пропускания):

 

 

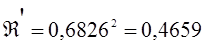
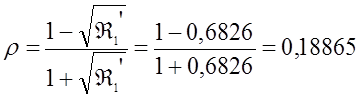
Выбираем заранее фильтр 2-го класса по сопротивлению и определяем затухание несогласованности в полосе пропускания

 

 

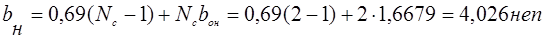
и затухание эха

 

После определяем величину отклонения  характеристического сопротивления от номинального в полосе пропускания

 

 

Что удовлетворяет исходным техническим требованиям. Таким образом, на основании проведенного расчета выбран фильтр 2-го класса по сопротивлению с числом звеньев N=4. Отклонение характеристического сопротивления от номинального в полосе пропускания составляет 3,558 %, коэффициент использования полосы пропускания =0,885, теоретическая частота среза =113,016 кгц.

Расчетные параметры необходимые в дальнейшем,

 

=0,43 =0,4659 =113,016 кгц.

 

Так как фильтр состоит из четырех звеньев, то для каждого звена рассчитываем коэффициент  и соответственно расчетный параметр m.

 

где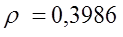

 

=1,2,3,4 - № звена

N= 4 – число звена

 

Таким образом

 

 

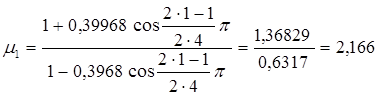
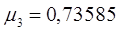
Проверкой правильности расчета при четном числе звеньев служит соблюдение следующих соотношений:

 

,  и т.д.

т.е. в рассматриваемом примере 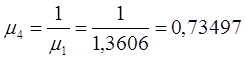 и т.д.

Для расчета коэффициентов m полагаем, что =0,43, тогда

 

 

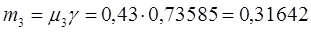
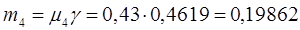
Затем определяем

 

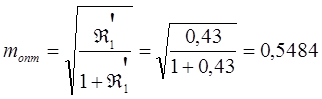
Для получения наилучшего согласования фильтра с нагрузкой начинаем и оканчиваем фильтр полузвеньями, у которых значение коэффициента m ближе к . В рассматриваемом примере этому требованию удовлетворяет коэффициент .

Внутри фильтра звенья с различными коэффициентами  могут соединяться в произвольном порядке, но при условии соблюдения согласования.

Затем приступаем к выбору конкретной схемы фильтра нижних частот. При этом нужно стремиться к выбору звеньев с наименьшим числом катушек индуктивности, поскольку именно эти элементы наиболее усложняют производство и настройку фильтра. Так как класс фильтра определяется классом конечных полузвеньев, то для них выбираем звено типа 2А1н (звено Т-образного вида, 2-го класса по сопротивлению, с одной стороной среза фильтра нижних частот) и делим его пополам, для того, чтобы не увеличивать общее число звеньев. При этом получаются оконечные полузвенья Г-образного вида. В качестве промежуточных звеньев используем звенья типа 1В1н (звено П-образного вида, первого класса по сопротивлению, с одной частотой среза, фильтра нижних частот). Далее составляем полную принципиальную схему всего фильтра нижних частот рисунок 8.

 

звена 2А1н 1В1н 1В1н1В1н звена 2А1н

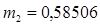
Рисунок 8 – Полная принципиальная схема фильтра нижних частот

 

Первый этап расчета заканчиваем вычислением частот минимального затухания, лежащих в полосе задерживания.

 

 

соответственно

 

 

 

 

Формула для расчета частот минимального затухания

 

 

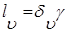Аналогично формуле для расчета  с той лишь разницей, что вместо параметра  подставляется . Коэффициент , аналогичный коэффициенту , рассчитывается по формуле

 

 

где =1,2,3,4 – № звена

N= 4 – число звеньев

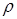=0,3986 – ранее определенный параметр

Таким образом

 

 

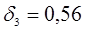
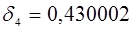
Проверка правильности расчета коэффициентов :

 

,  и т.д.

где

т.е. в рассматриваемом примере  и т.д.

Далее для каждого звена определяем параметр и частоту минимального затухания:

 

 

 

 

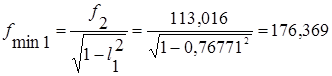
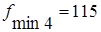
Частота последнего минимума затухания должна совпадать с верхней граничной частотой полосы задерживания. Кроме того должно соблюдаться строгое чередование частот бесконечного и минимального затухания. Правильность расчета подтверждается в рассматриваемом примере равенством и таблицей 1.

 

Таблица 1

Частота, кгц	1 звено	2 звено	3 звено	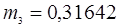4 звено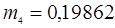
	310,442	139,356	119,137	115,313
	176,369	125,179	116,4189	115

 

Заметим, что наибольшему значению m соответствует наиболее удаленная от полосы пропускания частота бесконечного затухания, а наименьшему значению m соответствует ближайшая к переходной области частота бесконечного затухания. Все частоты  и  находятся в полосе задерживания. Не допускается расположение частот  и  в полосе пропускания.

Определив частоты бесконечного и минимального затухания, а так же значения коэффициентов  для всех звеньев и составив полную принципиальную схему фильтра нижних частот (ФНЧ состоит из трех звеньев типа 1В1н и двух полузвеньев типа 2А1н), приступаем к расчету номинальных значений элементы схемы ФНЧ. Начинаем с определения величины расчетного сопротивления , а затем единичной индуктивности и единичной емкости .

Коэффициент нагрузки  рассчитывается графоаналитическим способом. Суть расчета сводится к тому, что выбирается такое соотношение между сопротивлением нагрузки и номинальным характеристическим сопротивлением, при котором в заданной полосе частот обеспечивается наилучшее согласование. Расчет характеристического сопротивления ведется только для оконечного полузвена, ибо если выполняются условия согласования характеристического сопротивления с сопротивлением нагрузки для оконечного полузвена на всех частотах полосы пропускания, то они выполняются и для всех промежуточных звеньев (данные расчета приведены в таблице 2).

 

Таблица 2

Оконечное полузвено Ом =113,016 кгц.
f, кгц
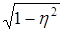
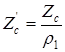
50	0,4424	0,8968	0,87128	1,02929	1029,29	1,03592
55	0,4867	0,8736	0,84421	1,0348	1034,8	1,0415
60	0,5309	0,8474	0,8146	1,04027	1040,27	1,04697
65	0,5751	0,81805	0,7825	1,0454	1045,4	1,0521
70	0,6194	0,7851	0,7477	1,0500	1050,0	1,0568
75	0,6636	0,7481	0,71037	1,05311	1053,11	1,053865
80	0,7079	0,7064	0,6704	1,05369	1053,69	1,0605
85	0,7521	0,6590	0,62797	1,0494	1049,4	1,0562
90	0,7964	0,6048	0,58285	1,03766	1037,66	1,0443
95	0,8406	0,5417	0,53526	1,01203	1012,03	1,01855
100	0,8848	0,4659	0,48511	0,9604	960,4	0,9666

 

Коэффициент согласования  – это отношение характеристического сопротивления к сопротивлению нагрузки, т.е. . Чем меньше коэффициент согласования отличается от единицы, тем лучше согласованы характеристическое сопротивление и сопротивление нагрузки. Графоаналитический метод заключается в симметрировании кривой  относительно значения  (т.е. уравнивания наибольшего и наименьшего значений 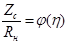в полосе пропускания).

Исходя из этого, определяется коэффициент нагрузки , позволяющий затем вычислить  как оптимальное номинальное характеристическое сопротивление. Проводя симметрирование, перемещаем кривую  вдоль оси ординат относительно значения (в рассматриваемом примере вниз) так, чтобы максимальное положительное и максимальное отрицательное отклонения функции 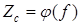 от значения  были приблизительно равны.

 

Рисунок 9 – График симметрирования характеристического сопротивления ФНЧ

В рассматриваемом примере экспериментальное значение функции  соответствует значениям  и . На частоте  коэффициент согласования 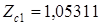. На частоте  коэффициент согласования .

Из этого обобщенного графика можно сделать заключение о форме характеристики затухания фильтра нижних частот. Положительное отклонение  от значения  свидетельствует об обеспечении неискаженной передачи частот полосы пропускания в диапазоне частот  и ; отрицательное отклонение свидетельствует о наличие искажений для некоторых частот полосы пропускания (наблюдается так называемый завал фронтов амплитудно-частотной характеристики).

Максимально положительное и максимально отрицательное отклонение на этих частотах составляют соответственно ()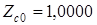

 

 

 

Разность отклонений

 

 

Среднее отклонение

 

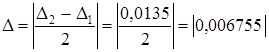
Новое значение коэффициента согласования на частоте  с учетом среднего отклонения

 

 

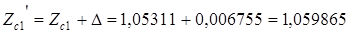
Коэффициент несогласованности и коэффициент нагрузки 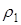 на частоте  соответственно равны

 

 

 

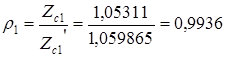
Полагая коэффициент нагрузки  на частотах и  одинаковым, находим коэффициент согласования и коэффициент несогласованности на частоте :

 

 

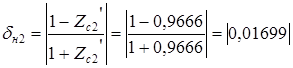
Так как значения и ничтожно мало отличаются друг от друга, коэффициент нагрузки выбираем окончательно .

Определяем расчетное характеристическое сопротивление

Ом

 

Следует отметить, что, так как  и мало отличается от , можно было бы пренебречь несогласованностью при расчете и  полагать Ом.

Вычисляем величины единичной индуктивности  и единичной емкости исходного звена типа .

 

 

 

, ,

Рисунок 10 – Расчетные соотношения для П-образного звена типа 1В1н фильтра нижних частот.

 

Учитывая составленную полную принципиальную схему фильтра нижних частот (см. рисунок 8), рассчитываем номинальные величины элементов каждого звена схемы. Звено типа 1В1н рассчитывается следующим образом:

 

 

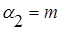
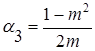
Зная коэффициенты и можно рассчитать элементы всех звеньев (рисунок 10), учитывая при этом, что для каждого звена требуются свои значения m, а значения и постоянны для всех звеньев. Расчет дается для одного типового промежуточного звена и оконечного полузвена. Значения элементов остальных звеньев сведены в таблице 3.

123	Поделиться:

Воспользуйтесь поиском по сайту: