Пределы применимости формулы Эйлера

Задача Эйлера

 

Рассмотрим центрально сжатый шарнирно закрепленный с обоих концов стержень. Эта задача была решена Л. Эйлером.

Существо задачи состоит в том, что задача об устойчивости по отношению к заданному возмущению подменяется задачей о возможности существования двух различных форм равновесия при одном и том же значении силы F. Очевидно, что прямолинейная равновесная форма возможна (y = 0). Допустим, что наряду с прямолинейной равновесной формой возможна и криволинейная равновесная форма, показанная на рисунке.

 

 

Кривизна стержня на основании закономерности известной из теории изгиба выразится

Будем полагать, что угол поворота y ’ – величина малая по сравнению с единицей и тем более мал квадрат этой величины по сравнению с единицей

Изгибающий момент в произвольном сечении с координатой Z:  (знак минус увязывает прогиба и кривизны).

Дифференциальное уравнение изогнутой оси выглядит

 

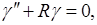
 или  (1)

 

Решение этого дифференциального уравнения хорошо известно

 

 

Из граничных условий попробуем найти произвольные постоянные

C₁ и С₂

1) при Z=0: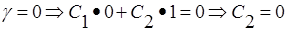

2) при Z= :

Возможны две ситуации

C₁=0, откуда y 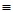0, т. е. получаем прямолинейную равновесную форму,

Sin K  (n N) подставим в (1) выражение R² =  

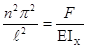 откуда найдем значение силы, при которой помимо прямолинейной равновесной формы появляется смежная криволинейная равновесная форма

 

 

реальный смысл имеет наименьшее значение силы при n=1 эйлерова сила – критическая сила.

 

F_кр=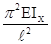

Очевидно, что I_x – минимальный момент инерции.

Потери устойчивости будет происходить по синусоиде y = C₁Sin

однако произвольную C₁ мы так и не смогли найти.

Дело в том, что задача о потере устойчивости задача существенно нелинейно, а мы поступили непоследовательно. С одной стороны мы подошли к задаче как нелинейной, отойдя от принципа начальных размеров, и определив изгибающий момент с учетом изгиба стержня. С другой стороны, приняв приближенное выражение для кривизны, мы линеаризовали задачу. Для того, чтобы определить прогибы в закритической стадии надо исходить из нелинейного дифференциального уравнения.

Однако главная цель – определение критической силы для стержня нами достигнута.

 

Влияние условий закрепления концов стержня на величину критической силы

Формула (2) даёт возможность определить критическую силу только в том случае шарнирного опирания обоих концов стержня. Обобщим полученный результат на некоторые другие часто встречающиеся случаи закрепления.

а). Стержень, закреплённый жёстко одним концом и свободный от закрепления на другом. Очевидно изгиб стержня в этом случае будет таким же, как и в случае шарнирно опертого стержня, но имеющего длину в 2 раза большую.

 

Критическая сила в этом случае будет равна критической силе шарнирно опёртого стержня, имеющего длину 2 .

Введём понятие коэффициента привидения длины -  , т. е. числа показывающего во сколько раз нужно увеличить длину шарнирно опёртого стержня, чтобы критическая сила для него равнялась критической силе стержня длиной  при заданном закреплении.

Очевидно, что в нашем случае коэффициент  можно трактовать, как число показывающее сколько раз длина стержня укладывается в длине полуволны синусоиды, по которой происходит потеря устойчивости.

Обобщим формулу Эйлера

 

                           (3)

 

Для некоторых других случаев закрепления коэффициент приведения длины равен:

Рис. 102

Пределы применимости формулы Эйлера

 

Формула Эйлера выведена в предположении, что материал линейно упруг, и, естественно, применила, в тех случаях пока справедлив закон Гука.

Придадим формуле (3) иной вид.

Введём понятие критического напряжения, т. е. напряжения соответствующего критической силе.

 

;  (4)

 

но  где 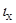 - минимальный радиус инерции сечения.

Введём ещё одну величину – гибкость стержня.

 

, тогда

Тогда можно оказать, что формула Эйлера справедлива, если критические напряжения не превышают предела пропорциональности при сжатии.

 

 

Выясним при каких гибкостях можно использовать формулу Эйлера.

Приравняем в (4)

 

 =

 

Если 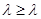, то можно использовать формулу (3)

Для малоуглеродистых сталей, особенно часто используемых для сжатых элементов: МПа, E = 2*10⁵ МПа тогда,

 т.е. для малоуглеродистых сталей формулу Эйлера можно использовать при гибкостях больших 100.

 

12	Поделиться:

Воспользуйтесь поиском по сайту: