 |
Определение параметров рассчитанного трансформатора
|
|
|
|
4.1. Вес активных материалов
4.1.1. Вес материала обмоток.
4.1.1.1. Расчет веса металла обмотки низкого напряжения.
Вес металла обмотки низкого напряжения:
 , кг, , кг,
| (31) |
В формуле (31) l срН – длина среднего витка обмотки низкого напряжения, которая, при ступенчатой форме сечения стержня определяется по формуле:
 , мм, , мм,
| (32) |
при прямоугольном сечении стержня:
 , мм. , мм.
| (33) |
gм– удельный вес материала проводника; для меди – 89×10-7 кг/мм3, для алюминия – 27×10-7 кг/мм3.
4.1.1.2. Расчет веса металла обмотки высокого напряжения.
Вес металла обмотки высокого напряжения:
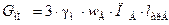 , кг. , кг.
| (34) |
Длина среднего витка обмотки высокого напряжения при ступенчатой форме сечения стержня:
 , мм, , мм,
| (35) |
при прямоугольной форме сечения стержня:
 , мм. , мм.
| (36) |
4.1.1.3. Общий вес материала обмоток.
 , кг. , кг.
| (37) |

4.1.2. Вес стали сердечника.
Для упрощения последующих расчетов целесообразно в объеме магнитной системы трансформатора выделить следующие основные части: объем стержня, имеющего длину, равную высоте окна – V с, объем ярма – V я, объем угла магнитной системы – V у (рис. 20 а) и дополнительный объем металла, занимающего пространство в месте соединения стержня и ярма – V д (рис. 20 б). Очевидно, что при прямоугольной форме сечения магнитопровода дополнительный объем отсутствует. Плоская стержневая магнитная система трехфазного трансформатора содержит шесть углов, понимаемых как части, ограниченные объемом, образованным пересечением боковых ступенчатых поверхностей одного из ярм и одного из стержней.
Вес стержня:
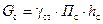 ,кг, ,кг,
| (38) |
где gст – удельный вес стали, 7650 кг/м3 – холоднокатаной, 7550 кг/м3 –горячекатанной.
Вес угла магнитной системы при прямоугольном сечении магнитопровода:
|
|
|
 , кг; , кг;
| (39) |
при ступенчатом сечении магнитопровода:
 , кг, , кг,
| (40) |
где V у – объем угла, определяемый по таблице 8.6 [1], см3. Для определения объема угла при d < 0,08 м необходимо аппроксимировать табличную зависимость кубической параболой, проходящей через начало координат.
Вес ярма:
 , кг, , кг,
| (42) |
где lя – длина ярма, м;
G д – вес дополнительного объема, кг.
Длина ярма при ступенчатом сечении:
 , мм. , мм.
| (42) |
при прямоугольном сечении:
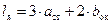 , мм. , мм.
| (43) |
Вес дополнительного объема при ступенчатой форме сечения магнитопровода:
 , кг, , кг,
| (44) |
Общий вес стали:
 , кг. , кг.
| (45) |
4.2. Потери в активных материалах.
4.2.1. Потери короткого замыкания.
Потери в проводниках обмотки, называемые потерями короткого замыкания, с учетом добавочных потерь, могут быть определены по формуле
 , Вт, , Вт,
| (46) |
где  – вес материала обмотки высокого или низкого напряжения, кг;
– вес материала обмотки высокого или низкого напряжения, кг;
k м – величина, определяемая свойствами материала проводника; для меди k м = 2,4 Ом×м4/кг, для алюминия – k м = 12,75 Ом×м4/кг.
Средний коэффициент добавочных потерь для обмотки из прямоугольного провода может быть вычислен по формуле:
 , ,
| (47) |
для обмотки из круглого провода:
 . .
| (48) |
В двух последних формулах
f – частота напряжения, Гц;
r – удельное электрическое сопротивление обмоток для 750С, мкОм/м (rМ75=0,02135 мкОм/м, rА75=0,0344 мкОм/м);
n – число слоев обмотки по ширине окна;
m – число витков обмотки по высоте окна;
l – размер сечения проводника в осевом направлении (при намотке плашмя – больший размер), м;
r – размер сечения проводника в радиальном направлении (при намотке плашмя – меньший размер), м;
h об – высота обмотки, м;
d – диаметр проводника круглого сечения, м;
k р – коэффициент приведения поля рассеяния или коэффициент Роговского.
В зависимости от того, для какой обмотки ведется расчет, обозначение среднего коэффициента добавочных потерь должно быть дополнительно проиндексировано буквами "В" и "Н".
|
|
|
Формула (43) должна использоваться отдельно для каждой из обмоток с подстановкой соответствующих значений коэффициентов, плотности тока и веса материала. В результате расчетов должны быть получены потери в обмотке низкого напряжения – p мН и потери в обмотке высокого напряжения – p мВ. Суммарные потери короткого замыкания:
 , Вт. , Вт.
| (49) |
4.2.2. Потери холостого хода.
Основные потери в стали, называемые потерями холостого хода, в общем случае определяются по формуле
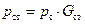 , Вт, , Вт,
| (50) |
где p c– удельные потери в одном килограмме стали стержня (ярма) для соответствующих индукций, определяемые по таблицам 8.9. и 8.10. [1].
В местах стыка полос электротехнической стали, образующих магнитопровод, имеет место увеличение потерь. Кроме этого, существуют добавочные потери, вызванные несовершенством магнитопровода. Указанные факторы учитываются в следующей формуле:
 , Вт, , Вт,
| (51) |
где k пд – коэффициент, учитывающий добавочные потери, вызванные резкой стали, снятием заусенцев, прессовкой магнитной системы и т.п., для отожженных пластин может быть принят равным 1,12, для неотожженных пластин – 1,22;
k пу – коэффициент увеличения потерь в углах магнитопровода, зависящий от марки стали и числа углов с прямыми и косыми стыками, выбираемый по таблице 8.13 [1].
4.2.3. Оценка нагрева обмоток.
4.2.3.1. Оценка нагрева цилиндрической обмотки из провода с прямоугольным сечением.
Для оценки нагрева обмотки необходимо определить плотность теплового потока на ее охлаждаемой поверхности:
 , Вт/м2, , Вт/м2,
| (52) |
где l – размер сечения проводника в осевом направлении (при намотке плашмя – больший размер), мм.
Обмотка не будет перегреваться, если полученная плотность теплового потока не превышает значения, приведенного в таблице 9.2б [1] для используемой ширины охладительного канала и класса нагревостойкости изоляции обмотки.
4.2.3.2. Оценка нагрева цилиндрической обмотки из провода с круглым сечением.
Плотность теплового потока на поверхности обмотки из проводника круглого сечения может быть определена по формуле:
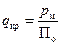 , Вт/м2, , Вт/м2,
| (53) |
где p м– потери мощности в проводниках обмотки высокого (pмВ) или низкого (p мН) напряжения;
По – площадь поверхности охлаждения обмотки.
|
|
|
Площадь поверхности охлаждения обмотки может быть вычислена по формуле:
 , м2. , м2.
| (54) |
где Пвн – внутренняя поверхность охлаждения цилиндрической катушки, м2;
Пнар – наружная поверхность охлаждения цилиндрической катушки, м2;
Птор – торцевая поверхность охлаждения цилиндрической катушки, м2;
k зкр – коэффициент, учитывающий закрытие части поверхности охлаждения рейками, для внутренней обмотки может быть принят равным 0,8, для внешней – 0,9. Впоследствии, при выполнении чертежа электромагнитной системы трансформатора, необходимо следить, чтобы не более 20 и 10 процентов поверхности обмоток низкого и высокого напряжения соответственно были закрыты конструкционными элементами.
При ступенчатой форме сечения стержня формула (54) преобразуется к виду:
 , м2. , м2.
| (55) |
В формуле (55) используются значения внутреннего и наружного диаметров обмотки – D вн и D нар, которые рассчитываются с учетом расположения обмоток по отношению к стержню. Для обмотки НН, лежащей ближе к стержню:
 , м2, , м2,
 ,м2, ,м2,
| (56) |
для обмотки ВН, лежащей снаружи:
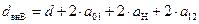 , м2, , м2,
 , м2, , м2,
| (57) |
При прямоугольной форме сечения стержня площади охлаждения катушек, входящие в выражение (54), для обмотки низкого напряжения вычисляются по формулам:
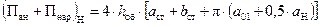 , м2, , м2,
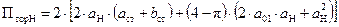 , м2; , м2;
| (58) |
для обмотки высокого напряжения – по формулам:
 , м2, , м2,
 , м2. , м2.
| (59) |
При использовании изоляции класса нагревостойкости А плотность теплового потока для наружной обмотки не должна превышать 600 Вт/м2. Допустимая плотность теплового потока для внутренней обмотки определяется с использованием таблицы 9.2б [1].
4.3. Напряжение короткого замыкания.
4.3.1. Активная составляющая.
 , %. , %.
| (60) |
4.3.2. Реактивная составляющая.
 , %. , %.
| (61) |
Величины b, ар и kp, используемые в формуле (61), должны быть вычислены точно, на основе данных, полученных на предыдущих этапах расчета.
Уточненное значение реактивной составляющей напряжения короткого замыкания не должно отличаться от заданного значения более чем на 10 %.
4.3.2.1. Уточнение b при круглом сечении стержня.
|
|
|
 , ,
| (62) |
где d12 – диаметр осевого канала между обмотками:
 , мм. , мм.
| (63) |
4.3.2.2. Уточнение bпри прямоугольном сечении стержня.
 , ,
| (64) |
где l ср– средняя длина витка двух обмоток:
 , мм. , мм.
| (65) |
4.3.2.3. Уточнение а ри k р.
 , м, , м,

| (66) |
4.3.3. Напряжение короткого замыкания.
 , %. , %.
| (67) |
4.4. Механические усилия и нагрев обмоток при коротком замыкании.
4.4.1. Установившийся ток короткого замыкания.
 , А. , А.
| (68) |
4.4.2. Ударный ток короткого замыкания.
 , А, , А,
| (69) |
где kmax – ударный коэффициент, определяемый по формуле:
 . .
| (70) |
4.4.3. Радиальная сила, действующая на обмотки.
 , Н , Н
| (71) |
4.4.4. Механическое напряжение сжатия обмотки низкого напряжения.
 , Па , Па
| (72) |
Полученное значение напряжения сжатия не должно превышать 30 МПа для меди и 15МПа для алюминия.
4.4.5. Температура обмотки высокого напряжения.
 , 0С, , 0С,
| (73) |
где t к – продолжительность короткого замыкания, принимается равной 3с;
Jнач – начальная температура обмотки, принимается равной 900С.
Полученное значение температуры не должно превышать допустимое значение, приведенное в таблице 7.6 [1].
4.5. Относительное изменение напряжения.
Значения относительного изменения напряжения должны быть определены для всего диапазона изменения угла нагрузки. По результатам расчетов необходимо построить график и выделить значение Du, соответствующее заданному углу нагрузки.
 , % , %
| (74) |
4.6. Ток холостого хода.
4.6.1. Активная составляющая тока холостого хода.
 ,%. ,%.
| (75) |
4.6.2. Полная мощность холостого хода.
Полная мощность холостого хода может быть определена по формуле:
 , Вт, , Вт,
| (76) |
где  – коэффициент, учитывающий влияние резки стальной полосы на пластины и влияние срезания заусенцев, для отожженных пластин из стали марок 3404 и 3405 принимается равным 1,2, для неотожженных пластин из стали тех же марок – 1,55;
– коэффициент, учитывающий влияние резки стальной полосы на пластины и влияние срезания заусенцев, для отожженных пластин из стали марок 3404 и 3405 принимается равным 1,2, для неотожженных пластин из стали тех же марок – 1,55;
 – коэффициент, учитывающий форму сечения ярма, прессовку магнитной системы и перешихтовку верхнего ярма, при ступенчатой форме сечения магнитопровода принимается равным 1,06, при прямоугольной форме сечения – 1,134;
– коэффициент, учитывающий форму сечения ярма, прессовку магнитной системы и перешихтовку верхнего ярма, при ступенчатой форме сечения магнитопровода принимается равным 1,06, при прямоугольной форме сечения – 1,134;
 – коэффициент, учитывающий увеличение намагничивающей мощности в углах магнитной системы, определяется по формуле(77);
– коэффициент, учитывающий увеличение намагничивающей мощности в углах магнитной системы, определяется по формуле(77);
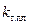 – коэффициент, учитывающий ширину пластин в углах магнитной системы, определяется по таблице 8.21 [1];
– коэффициент, учитывающий ширину пластин в углах магнитной системы, определяется по таблице 8.21 [1];
q з – полная удельная намагничивающая мощность в зоне шихтованного стыка, определяется по таблице 8.17 [1];
Пз – площадь зазора, равная площади поперечного сечения стержня, м2.
Для определения коэффициента  трехфазного трансформатора с плоской магнитной системой следует воспользоваться формулой
трехфазного трансформатора с плоской магнитной системой следует воспользоваться формулой
 , ,
| (77) |
где  и
и  – коэффициент
– коэффициент  , определенный для стыков крайних стержней и среднего стержня соответственно, по таблице 8.19 [1].
, определенный для стыков крайних стержней и среднего стержня соответственно, по таблице 8.19 [1].
|
|
|
Если в трансформаторе все стыки прямые, формула (77) принимает вид
 , ,
| (78) |
где 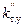 – коэффициент
– коэффициент  , определенный по таблице 8.19 [1] для прямых стыков, используемой марки стали и индукции в стержне.
, определенный по таблице 8.19 [1] для прямых стыков, используемой марки стали и индукции в стержне.
4.6.3. Полный ток холостого хода.
Относительное значение полного тока холостого хода может быть определено по формуле
 , % , %
| (79) |
4.6.4. Реактивная составляющая тока холостого хода.
Реактивная составляющая тока холостого хода – ток намагничивания трансформатора – может быть определена по формуле
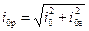 , %. , %.
| (80) |
4.7.Схема замещения трансформатора.
4.7.1. Полное сопротивление холостого хода:
 , Ом, , Ом,
| (81) |
где  – ток холостого хода первичной обмотки, А.
– ток холостого хода первичной обмотки, А.
4.7.2. Активное сопротивление холостого хода:
 , Ом. , Ом.
| (82) |
4.7.3. Индуктивное сопротивление холостого хода:
 , Ом. , Ом.
| (83) |
4.7.4. Полное сопротивление короткого замыкания:
 , Ом, , Ом,
| (84) |
где  – напряжение короткого замыкания, В.
– напряжение короткого замыкания, В.
4.7.5. Активное сопротивление короткого замыкания:
 , Ом. , Ом.
| (85) |
4.7.6. Индуктивное сопротивление короткого замыкания.
 , Ом. , Ом.
| (86) |
4.7.7. Определение величин сопротивлений схемы замещения.
Считая, что r 1= r 2/и x1= x 2 /, можно записать:
 , Ом, , Ом,
| (87) |
откуда
 , Ом, , Ом,
| (88) |
и
 , Ом. , Ом.
| (89) |
Сопротивления схемы замещения показаны на рисунке 21.
4.8. Коэффициент полезного действия.
В общем случае КПД трансформатора определяется по формуле
 , ,
| (90) |
где k нг – отношениерабочего тока обмотки к номинальному току – коэффициент нагрузки.
 |
Расчеты зависимости КПД от коэффициента нагрузки, изменяющегося в диапазоне от 0 до 1,2, необходимо произвести для cos j2 = 1 и cos j2, приведенного в задании на курсовой проект. Результаты расчетов должны быть представлены в виде графика.
При cos j2 = 1 и номинальной нагрузке трансформатора расчетное значение КПД не должно расходиться с заданным более чем на 5%.
|
|
|


