 |
Тема: Системы линейных уравнений.
|
|
|
|
К системам линейных уравнений приводит множество прикладных, в том числе и экономических задач. Система  линейных уравнений с
линейных уравнений с  переменными имеет вид:
переменными имеет вид:  .
.
Где  - произвольные числа, причем
- произвольные числа, причем  . Числа
. Числа  называются соответственно коэффициентами при переменных и свободными членами уравнений.
называются соответственно коэффициентами при переменных и свободными членами уравнений.
Решением системы линейных уравнений называется такая совокупность  чисел
чисел 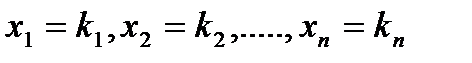 , при подстановке которых каждое уравнение системы обращается в верное равенство.
, при подстановке которых каждое уравнение системы обращается в верное равенство.
 Матричный метод
Матричный метод
Запишем систему линейных уравнений в матричной форме. Обозначим:
 ,
, 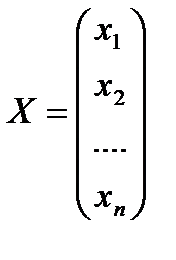 ,
,  , где
, где
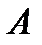 – матрица коэффициентов при переменных, или матрица системы,
– матрица коэффициентов при переменных, или матрица системы,
 – матрица – столбец переменных,
– матрица – столбец переменных,
 – матрица – столбец свободных членов.
– матрица – столбец свободных членов.
Тогда систему линейных уравнений можно записать в виде: 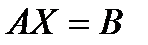 .
.
Пусть число уравнений системы равно числу неизвестных, то есть  . Тогда матрица системы является квадратной, а ее определитель
. Тогда матрица системы является квадратной, а ее определитель  называется определителем системы. Если квадратная матрица системы
называется определителем системы. Если квадратная матрица системы  невырожденная, то есть ее определитель
невырожденная, то есть ее определитель  , то существует обратная матрица
, то существует обратная матрица  . Тогда справедливо:
. Тогда справедливо: 


|
Последняя формула позволяет решить систему 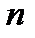 линейных уравнений с
линейных уравнений с  неизвестными методом обратной матрицы.
неизвестными методом обратной матрицы.
 Пример1. Решить систему уравнений
Пример1. Решить систему уравнений  методом обратной матрицы.
методом обратной матрицы.
Решение.
а) Обозначим
 .
.
Тогда в матричной форме данная система имеет вид: 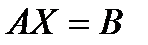 .
.
1) Найдем определитель: 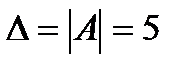 .
.
2) Так как  , то матрица
, то матрица 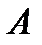 невырожденная, и существует обратная матрица
невырожденная, и существует обратная матрица  . Найдем
. Найдем  .
.
 .
.
3) Для решения системы воспользуемся формулой  . Получим:
. Получим:
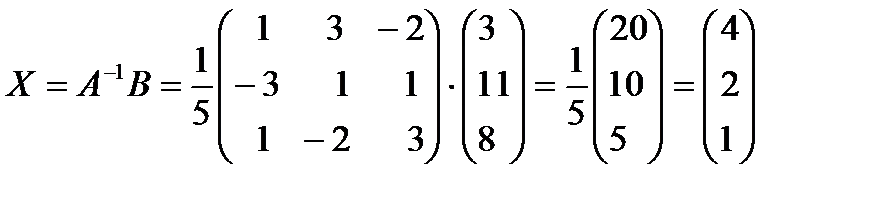
То есть решение системы (4; 2; 1).
4) Сделаем проверку: 
 №1 Решите систему линейных уравнений
№1 Решите систему линейных уравнений 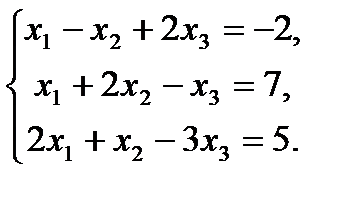 матричным методом.
матричным методом.
Решение:
 Метод Крамера
Метод Крамера
Теорема Крамера. Пусть  – определитель матрицы системы
– определитель матрицы системы  , а
, а 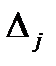 – определитель матрицы, получаемой из матрицы
– определитель матрицы, получаемой из матрицы  заменой
заменой 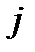 - го столбца столбцом свободных членов. Тогда, если
- го столбца столбцом свободных членов. Тогда, если  , то система имеет единственное решение, определяемое по формулам:
, то система имеет единственное решение, определяемое по формулам:
|
|
|
Эти формулы получили название формул Крамера.

|
 Пример2. Решить систему уравнений
Пример2. Решить систему уравнений  по формулам Крамера.
по формулам Крамера.
Решение.
а) Обозначим
 .
.
1) Найдем определитель: 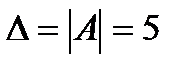 . Так как
. Так как  , то по теореме Крамера система имеет единственное решение.
, то по теореме Крамера система имеет единственное решение.
2) Вычислим определители матриц 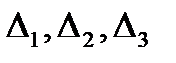 .
.
 ;
;  ;
;  .
.
3) Воспользуемся формулами Крамера:
 ;
; 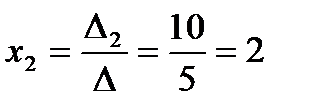 ;
;  ;
;
То есть решение системы (4; 2; 1).
4) Сделаем проверку: 
 №2 Выберите один вариант ответа и подчеркните его
№2 Выберите один вариант ответа и подчеркните его
Переменная х системы уравнений  определяется по формуле …
определяется по формуле …
ВАРИАНТЫ ОТВЕТОВ:
| 1) | 
| 2) | 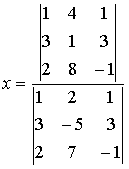
| |
| 3) | 
| 4) | 
|
 №3 Выберите один вариант ответа и подчеркните его
№3 Выберите один вариант ответа и подчеркните его
При решении системы 
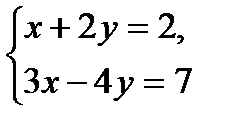 по правилу Крамера …
по правилу Крамера …
ВАРИАНТЫ ОТВЕТОВ:
1)  ; 2)
; 2) 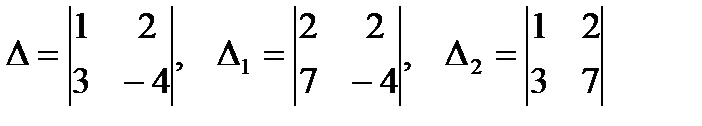 ;
;
3)  ; 4)
; 4)  ;
;
5) 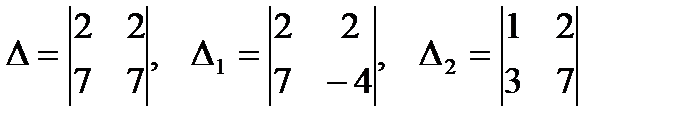 ;
;
 №4 Решите систему линейных уравнений
№4 Решите систему линейных уравнений 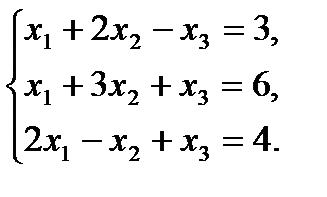 методом Крамера
методом Крамера
Решение:
 Метод Гаусса
Метод Гаусса
Метод Гаусса – метод последовательного исключения неизвестных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних переменных, находятся все остальные переменные. Переход системы к равносильной ей системе ступенчатого (или треугольного) вида называется прямым ходом, а нахождение переменных из системы – обратным ходом.
Преобразования Гаусса удобно проводить, осуществляя преобразования не с самими уравнениями, а с матрицей их коэффициентов.
Матрица  называется расширенной матрицей системы, ибо в нее, кроме матрицы системы, дополнительно включен столбец свободных членов.
называется расширенной матрицей системы, ибо в нее, кроме матрицы системы, дополнительно включен столбец свободных членов.
Алгоритм решения систем с помощью метода Гаусса.
Прямой ход:
- Составить расширенную матрицу системы.
- Выбрать ведущую строку, а в ней отличный от нуля ведущий элемент.
- В столбце ведущего элемента с помощью элементарных преобразований все остальные элементы обратить в нуль.
- а) Если в полученной матрице появилась строка
 , где
, где  , преобразования прекратить, ток как исходная система несовместна.
, преобразования прекратить, ток как исходная система несовместна.
б) Если такой строки не появилось, вычеркнуть (если есть) строки, все элементы которых равны нулю.
|
|
|
в) Снова выбрать ведущую строку среди строк, которые еще не были ведущими, а в ней ведущий элемент и повторить п. 3 и 4. В случае совместной системы каждая строка должна побывать ведущей
- Каждую строку разделить на соответствующий ведущий элемент.
В результате прямого хода будет получена расширенная матрица треугольного или ступенчатого вида или установлена несовместность системы.
Обратный ход.
По полученной в результате прямого хода матрице записать соответствующую систему, из которой последовательно, начиная с последних переменных, найти все остальные переменные.
 Пример 3.Методом Гаусса решить систему уравнений:
Пример 3.Методом Гаусса решить систему уравнений:

Решение. Прямой ход. Преобразуем расширенную матрицу системы

 ~
~ 
 ~
~ 

 .
.
Так как 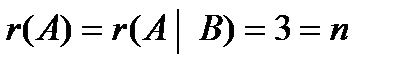 , то система совместна и определенна, то есть имеет единственное решение.
, то система совместна и определенна, то есть имеет единственное решение.
По полученной в результате прямого хода матрице записываем соответствующую систему, из которой последовательно, начиная с последних переменных, находим все остальные переменные.

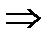
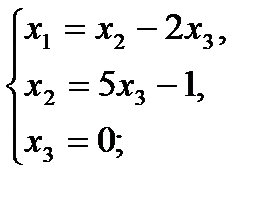
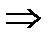

То есть решение системы (-1; -1; 0).
Сделаем проверку: 
Ответ: система совместна и определенна; (-1; -1; 0).
 Пример 4. Методом Гаусса решить систему уравнений:
Пример 4. Методом Гаусса решить систему уравнений:
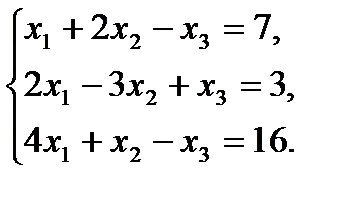
Решение. Преобразуем расширенную матрицу системы
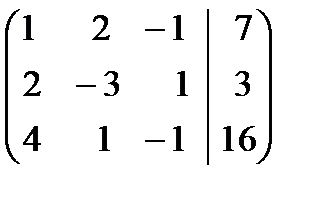
 ~
~ 
 ~
~  .
.
Итак, уравнение, соответствующее третьей строке последней матрицы, противоречиво – оно привелось к неверному равенству  , следовательно, данная система несовместна.
, следовательно, данная система несовместна.
 №5 Установите соответствие между системой линейных уравнений и ее расширенной матрицей с помощью
№5 Установите соответствие между системой линейных уравнений и ее расширенной матрицей с помощью
1. 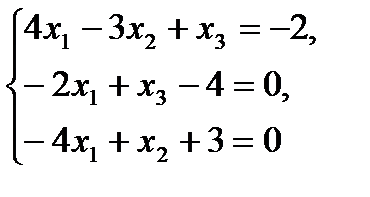 А
А 
2. 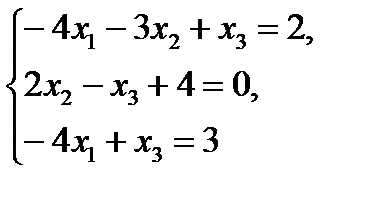 Б
Б 
3. 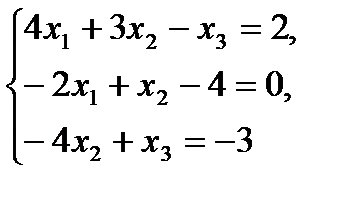 В
В 
4. 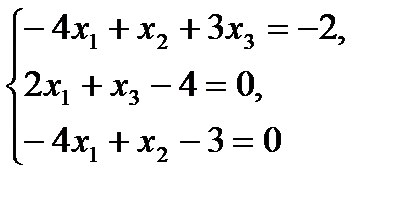 Г
Г 
Д 
Е 
 №6 Решите систему линейных уравнений
№6 Решите систему линейных уравнений 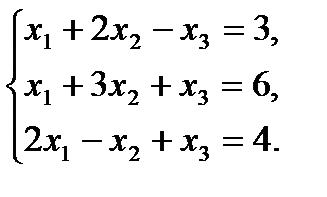 методом Крамера
методом Крамера
Решение:
|
|
|


