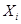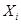 |
Проверка теоремы о разложении дисперсии
|
|
|
|
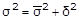
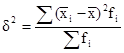
По 1 группе:
Таблица 2.3 Промежуточные показатели
|
|
|
|
| 16327 | -22293,16 | 496984982,8 |
| 30406 | -8214,16 | 67472424,51 |
| 32639 | -5981,16 | 35774274,95 |
| 15127 | -23493,16 | 551928566,8 |
| 38174 | -446,16 | 199058,7456 |
| 59320 | 20699,84 | 428483376 |
| 60425 | 21804,84 | 475451047,4 |
| 29994 | -8626,16 | 74410636,35 |
| 68499 | 29878,84 | 892745079,7 |
| 43512 | 4891,84 | 23930098,59 |
| 88196 | 49575,84 | 2457763912 |
| 18199 | -20421,16 | 417023775,7 |
| 74326 | 35705,84 | 1274907010 |
| 51639 | 13018,84 | 169490194,9 |
| 23959 | -14661,16 | 214949612,5 |
| 11916 | -26704,16 | 713112161,3 |
| 22226 | -16394,16 | 268768482,1 |
| 32579 | -6041,16 | 36495614,15 |
| 16320 | -22300,16 | 497297136 |
| Итого |
| 9097187445 |
По 2 группе:
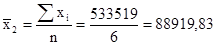
Таблица 2.4 Промежуточные показатели
|
|
|
|
| 37634 | -51285,83 | 2630236359 |
| 66707 | -22212,83 | 493409816,6 |
| 143321 | 54401,17 | 2959487297 |
| 55840 | -33079,83 | 1094275153 |
| 105129 | 16209,17 | 262737192,1 |
| 124888 | 35968,17 | 1293709253 |
| Итого |
| 8733855071 |
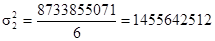
По 3 группе:
Таблица 2.5 Промежуточные результаты
|
|
|
|
| 125957 | -173682,67 | 30165669858 |
| 213881 | -85758,67 | 7354549480 |
| 559081 | 259441,33 | 67309803712 |
| Итого |
| 104830023050 |
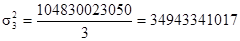
По 4 группе:
Таблица 2.6 Промежуточные результаты
|
|
|
|
| 71134 | -69309,5 | 4803806790 |
| 209753 | 69309,5 | 4803806790 |
| Итого |
| 9607613581 |
По 5 группе:
Таблица 2.7 Промежуточные результаты
|
|
|
|
| 174789 | 0 | 0 |
| Итого | - | 0 |
Средняя из внутригрупповых дисперсий:
Межгрупповая дисперсия:
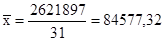
Таблица 2.8 Промежуточные показатели
|
|
|
|
|
| 38620,16 | -45957,16 | 2112060555 | 40129150550 |
| 88919,83 | 4342,51 | 18857393,1 | 113144358,6 |
| 299639,67 | 215062,35 | 46251814388 | 1,38755E+11 |
| 140443,5 | 55866,18 | 3121030068 | 6242060136 |
| 174789 | 90211,68 | 8138147208 | 8138147208 |
| Итого | - | - | 1,93*1011 |
Общая дисперсия по правилу сложения:
Общая дисперсия по формуле:
= 
Среднее значение дисперсии:
Таблица 2.9 Промежуточные показатели
|
|
|
| ||
| 174789 | 90211,68 | 8138147208
| ||
| 16327 | -68250,32 | 4658106180 | ||
| 30406 | -54171,32 | 2934531911 | ||
| 32639 | -51938,32 | 2697589084 | ||
| 15127 | -69450,32 | 4823346948 | ||
| 38174 | -46403,32 | 2153268107 | ||
| 59320 | -25257,32 | 637932213,6 | ||
| 60425 | -24152,32 | 583334561,4 | ||
| 29994 | -54583,32 | 2979338822 | ||
| 68499 | -16078,32 | 258512374 | ||
| 43512 | -41065,32 | 1686360507 | ||
| 88196 | 3618,68 | 13094844,94 | ||
| 18199 | -66378,32 | 4406081366 | ||
| 74326 | -10251,32 | 105089561,7 | ||
| 51639 | -32938,32 | 1084932924 | ||
| 23959 | -60618,32 | 3674580720 | ||
| 11916 | -72661,32 | 5279667424 | ||
| 125957 | 41379,68 | 1712277917 | ||
| 71134 | -13443,32 | 180722852,6 | ||
| 37634 | -46943,32 | 2203675293 | ||
| 66707 | -17870,32 | 319348336,9 | ||
| 22226 | -62351,32 | 3887687106 | ||
| 143321 | 58743,68 | 3450819940 | ||
| 213881 | 129303,68 | 16719441662 | ||
| 55840 | -28737,32 | 825833560,8 | ||
| 32579 | -51998,32 | 2703825283 | ||
| 16320 | -68257,32 | 4659061734 | ||
| 209753 | 125175,68 | 15668950863 | ||
| 559081 | 474503,68 | 2,25154E+11 | ||
| 105129 | 20551,68 | 422371550,8 | ||
| 124888 | 40310,68 | 1624950922 | ||
| Итого |
| 3,25647E+11 |
= 
+ 
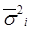-Теорема о разложении дисперсии.
10504729810 = 6237998239+4266731585 = 10504729824
Из проведённых расчётов видно, что общие дисперсии, рассчитанные различными способами, имеют небольшое отклонение, что и требовалось доказать.
Найти коэффициент детерминации
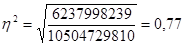
Вывод: фактор численности постоянного населения повлиял на производство промышленной продукции на 77%.
Задание №3
А Пределы, за которые не выйдет среднее значение признака
Т.к. по условию отбор – 35% бесповторный, и объем выборочной совокупности – 31 элементов, то объем генеральной совокупности будет равен 89 элементов(N). Т.к. p=0,954, то t=2.
Средняя ошибка выборки:
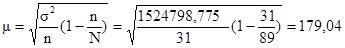
Предельная ошибка выборки:
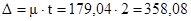
Таким образом:
=2089,64
Вывод: с вероятностью 0,954 можно утверждать, что численность постоянного населения на конец года колеблется в пределах 1731,56 – 2447,72 тыс. чел.
3.1.б Определение объема выборки для снижения предельной ошибки средней величины на 50%
Т.к. коэффициент доверия в данном случае является постоянным, то при снижении предельной ошибки выборки на 50% средняя ошибка выборки также уменьшится на 50%.
n = t2 
2N/(Δ2N + t2 
2), где:
n – объём выборочной совокупности;
t - коэффициент доверия;
|
|
|
- среднее квадратическое отклонение;
N – объём генеральной совокупности;
Δ – предельная ошибка выборки;
t=2
Предельная ошибка равна 358,08 тыс. чел., если мы её снизим на 50% то она будет равна 179,04 тыс. чел.
Объём выборочной совокупности n = 31, после снижения предельной ошибки на 50% n – изменится.
n = 
= 
= 
= 60,636
Вывод: Объем выборочной совокупности необходимо увеличить до 60,636 (61) элементов.
А Определение пределов, за которые не выйдет значение доли предприятий с индивидуальными значениями, превышающими моду
В данном случае отбор повторный, выберем p=0,683; тогда t=1; количество предприятий с индивидуальными значениями признака, превышающими моду, равно 27.
Mo=17169,8 кг
Их доля равна:
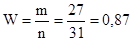
Предельная ошибка выборки равна:
Таким образом:
т.е.:
Вывод: значение доли предприятий с индивидуальными значениями, превышающими моду, находятся в интервале от 0,81% до 0,93%.
3.2.б Определение объема выборки для снижения предельной ошибки доли на 20%
Предельная ошибка выборки:
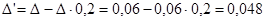
Имеем:
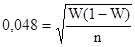
тогда n=49,1
Вывод: для снижения предельной ошибки на 20% необходимо увеличить объем выборки до 49,1 (49) элементов.
Задание №4
|
|
|
