 |
Сила давления жидкости на плоские поверхности
|
|
|
|
Сила давления жидкости на погруженную в нее плоскую поверхность (рис.2.9) равна
(2.12)
| где |
| Рисунок 2.9 – Схема для определения силы давления жидкости |
- глубина погружения центра тяжести смоченной части плоской поверхности; S-площадь смоченной части плоской поверхности;
- гидростатическое давление в центре тяжести поверхности.
Таким образом, полная сила давления на плоскую стенку равна произведению площади этой стенки на величину гидростатичес- кого давления в ее центре тяжести.
Выражение (2.11) можно представить в виде
(2.13)
где 
(2.14)
(2.15)
Сила 
представляет собой силу поверхностного давления 
. Поскольку давление распределено равномерно по всей площади смоченной части поверхности, его равнодействующая приложена в центре тяжести этой поверхности.
Сила 
обусловлена давлением самой жидкости. Сила 
приложена в центре давления Д, координату которого определяют по формуле
, (2.16)
где 
- момент инерции плоской фигуры относительно оси ОХ.
Для прямоугольника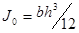 
(b-ширина, h-высота фигуры), для круга диаметром d 
.
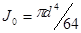Сила давления жидкости на криволинейные цилиндрические поверхности
Сила давления жидкости на криволинейную цилиндрическую поверхность (рис.2.10) складывается из горизонтальной 
и вертикальной 
составляющих
. (2.17)
|
| Рисунок 2.10 - Сила давления жидкости на криволинейную цилиндрическую поверхность |
Горизонтальная составляющая равна силе давления жидкости на вертикальную проекцию данной стенки
(2.18)
где 
- расстояние от свободной поверхности жидкости до центра тяжести ее вертикальной проекции; 
-площадь вертикальной проекции.
|
|
|
Вертикальная составляющая 
равна весу жидкости в объеме тела давления 
, т.е.
. (2.19)
Объем тела давления - объем, заключенный между данной стенкой, свободной поверхностью жидкости и вертикальными плоскостями, проходящими по контуру стенки.
Основы гидродинамики
Основные понятия о движении жидкости. Уравнение расхода (неразрывности)
Основной задачей гидродинамики является изучение законов движения жидкости.
Движение жидкости может быть установившимся и неустановившимся.
При установившемся движении жидкости скорость и давление во всех ее точках не изменяется с течением времени. При неустановившемся движении скорость и давление жидкости изменяются во времени.
При движении частиц жидкости различают линию тока, элементарную струйку, живое сечение.
Линией тока называется линия, касательная к каждой точке которой в данный момент времени совпадает с вектором скорости (рис.3.1).
| 
|
| Рисунок 3.1 – Линия тока | Рисунок 3.2 – Элементарная струйка |
Бесконечно малый объем, ограниченный линиями тока, называется элементарной струйкой. Предполагается, что поток движущейся жидкости состоит из отдельных элементарных струек.
Живое сечение потока - это поверхность в пределах потока жидкости, перпендикулярная в каждой своей точке к вектору соответствующей местной скорости в этой точке.
Расходом называется количество жидкости, протекающее через живое сечение в единицу времени. В гидравлике применяют объемный расход Q, 
:
(3.1)
где V-средняя скорость; S- площадь живого сечения.
При установившемся движении расход через все живые сечения потока одинаков:
. (3.2)
Выражение (3.2) называется уравнением расхода или уравнением неразрывности потока.
Уравнение Бернулли
|
|
|
Уравнение Бернулли является основным уравнением гидродинамики. Для двух сечений потока 1-1 и 2-2 реальной жидкости при установившемся движении уравнение Бернулли имеет вид
, (3.3)
где 
и 
- геометрический напор(удельная потенциальная энергия положения) в сечениях 1-1 и 2-2,м;
и 
- пьезометрический напор (удельная потенциальная энергия давления) в сечениях, м;
– скоростной напор (удельная кинетическая энергия) в сечениях, м;
, 
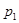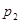- избыточное давление в сечениях, Па;
, 
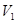- средние по живому сечению трубы скорости потока в сечениях, 
;
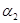- коэффициенты кинетической энергии(коэффициенты Кориолиса) в сечениях;
- плотность жидкости, 
;
-потери напора в трубе между сечениями, м.
|
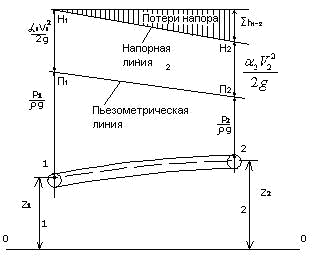
| Рисунок 3.3 – Графическая иллюстрация уравнения Бернулли |
Коэффициент кинетической энергии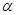 
учитывает неравномерность поля скоростей в рассматриваемом живом сечении. Величина этого коэффициента зависит от режима течения жидкости: для ламинарного течения 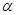=2, для турбулентного 
=1,05-1,15(
).
Все члены уравнения Бернулли в формуле (3.3) имеют линейную размерность и в энергетическом смысле представляют удельную энергию жидкости, т.е. энергию, отнесенную к единице веса жидкости.
Сумма всех трех членов 
+ 
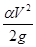=H представляет собой полный напор в сечениях.
Графическая иллюстрация уравнения Бернулли показана на рис.3.3. Линия 
показывает изменение полных напоров в сечениях 1-1 и 2-2 и называется напорной линией или линией полного напора, линия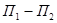 
- изменение пьезометрических напоров и называется пьезометрической линией.
Режимы движения жидкости
Силы вязкости в жидкости существенно влияют на величину и распределение скоростей движения жидкости, т.е. на характер ее движения.
Различают два режима движения: ламинарный и турбулентный. При ламинарном режиме жидкость движется отдельными слоями, пульсаций скоростей и давлений не наблюдается. Турбулентный режим характеризуется неупорядоченным, хаотичным движением частиц и интенсивным перемешиванием жидкости.
Критерием для определения режима движения является безразмерное число Рейнольдса. Для труб круглого сечения число Рейнольдса определяется по формуле
, (3.4)
где V – средняя скорость жидкости; 
- диаметр трубы;
|
|
|
- кинематический коэффициент вязкости жидкости.
Экспериментально определено, что режим будет ламинарным, если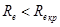 
.
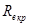- критическое число Рейнольдса, при котором происходит переход ламинарного режима в турбулентный. Для круглых труб принимают 
. Если число Рейнольдса находится в области 
, то режим считается переходным, а при 
- турбулентным.
Ламинарный режим возникает в тонких капиллярных трубках, во время движения очень вязких жидкостей, при фильтрации воды в слоях грунта и др. Движение маловязких жидкостей (вода, бензин, спирт) почти всегда происходит в турбулентном режиме.
|
|
|
