 |
Гидравлические сопротивления
|
|
|
|
Общие сведения о гидравлических потерях
Движение вязкой жидкости сопровождается потерями энергии.
Потери удельной энергии (напора), или гидравлические потери, зависят от формы, размеров русла, скорости течения и вязкости жидкости.
В большинстве случаев гидравлические потери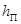 
пропорциональны скорости течения жидкости во второй степени или динамическому напору 
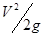и определяются из выражения
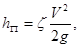(4.1)
где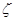 
- коэффициент потерь; V-средняя скорость в сечении.
Потери в единицах давления
. (4.2)
Гидравлические потери энергии обычно разделяют на местные потери и потери на трение по длине
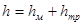. (4.3)
Местные потери энергии обусловлены так называемыми местными гидравлическими сопротивлениями, т.е. местными изменениями формы и размеров русла, вызывающими деформацию потока. При протекании жидкости через местные сопротивления изменяется ее скорость и возникают вихри.
Примером местных сопротивлений может служить задвижка (рис.4.1).
|
| Рисунок 4.1 – Местное гидравлическое сопротивление: а) задвижка |
Местные потери напора определяются по формуле Вейсбаха
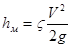, (4.4)
где V-средняя скорость в трубе;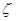 
-коэффициент местного сопротивления.
Потери на трение по длине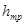 
-это потери энергии, которые возникают в прямых трубах постоянного сечения и возрастают прямо пропорционально длине трубы (рис.4.2).
Рассматриваемые потери обусловлены внутренним трением жидкости в трубах. Потери напора при трении определяются по формуле Дарси-Вейсбаха
, (4.5)
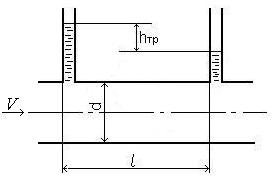
где λ – коэффициент гидравлического трения по длине или коэффициент Дарси; l – длина трубопровода; d –его диаметр; V – средняя скорость течения жидкости.
|
|
|
|
| Рисунок 4.2 – Потери напора по длине трубы |
Для ламинарного режима движения жидкости в круглой трубе коэффициент 
определяется по теоретической формуле
, (4.6)
где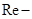 
число Рейнольдса.
При турбулентном режиме коэффициент 
зависит от числа Рейнольдса Re и относительной шероховатости 
(
-эквивалентная шероховатость) и определяется по эмпирическим формулам.
В области гидравлически гладких труб 4000<Re<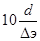 
, т.е. при малых скоростях и числах Рейнольдса, коэффициент Дарси зависит только от числа Рейнольдса, и его определяют по формуле Блазиуса
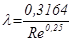. (4.7)
В переходной области (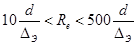
) на коэффициент Дарси влияют шереховатость и число Рейнольдса. В этой области для вычислений используют формулу Альтшуля
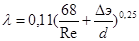. (4.8)
В квадратичной области сопротивления (области гидравлически шероховатых труб) коэффициент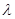 
может быть найден по формуле Шифринсона
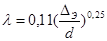. (4.9)
Местные сопротивления
В местных гидравлических сопротивлениях, вследствие изменения конфигурации потока на коротких участках, изменяются скорости движения жидкости по величине и направлению, а также образуются вихри. Это и есть причиной местных потерь напора. Местными сопротивлениями являются расширения и сужения русла, поворот, диафрагма, вентиль, кран и т.п. (рис.4.3).
Потери напора в местных сопротивлениях определяются по формуле (4.4).
При турбулентном режиме коэффициент 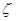зависит в основном от вида местного сопротивления, а при ламинарном- от числа Рейнольдса. Для всех местных сопротивлений этот коэффициент определяется экспериментально.
|
| Рисунок 4.3 – Местные гидравлические сопротивления: а – задвижка; б – диафрагма; в – поворот; г – вентиль |
Рассмотрим некоторые местные сопротивления.
Внезапное (резкое) расширение трубы (рис.4.4).
| При внезапном расширении трубы поток срывается с угла и постепенно расширяется. Между потоком и стенкой трубы образуются вихри, которые и являются причиной потерь энергии. Потери напора в этом случае определяют по теореме Борда
| ||
| Рисунок 4.4 – Внезапное расширение трубы |
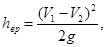(4.10)
где 
и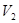 
- скорость жидкости впереди и после внезапного сужения.
Формулу (4.9) можно записать в виде:
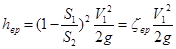. (4.11)
При этом для скорости 
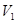
. (4.13)
При выходе жидкости из трубы в резервуар возникает резкое расширение потока. В этом случае 
>> 
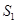(площадь резервуара значительно больше площади трубы).Коэффициент потерь на выходе из трубы будет: 
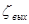=1.
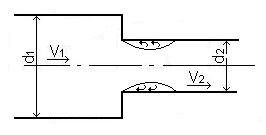
Внезапное сужение трубы (рис 4.5) вызывает меньшие потери энергии, чем внезапное расширение. В этом случае потери обусловлены трением потока при входе в узкую трубу и потерями на вихреобразование. Потери напора при внезапном сужении трубы определяют по формуле
(4.13)
где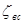 
определяется по формуле Идельчика
|
| Рисунок 4.5 – Внезапное сужение трубы |
При входе жидкости из резервуара в трубу можно считать 
, а коэффициент сопротивления равным 
Поворот трубы (рис 4.6) или колено без закругления вызывает
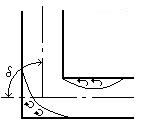
| значительные потери энергии, так как в нем происходят отрыв и вихреобразование, причем тем больше,чем больше
|
| Рисунок 4.6 – Поворот трубы |
.Потерю напора рассчитывают по формуле
(4.14)
где 
- коэффициент сопротивления колена, который определяется по справочным данным.
|
|
|
