Регрессионный и корреляционный анализ

Кафедра «Машины и технологическое оборудование»

 

 

Парный линейный

Регрессионный и корреляционный

Анализ

Экспериментальных данных

 

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению контрольной работы по дисциплинам

«Методология НИОКР»

и «Основы методологии научных исследований (ОМНИ)»

для студентов специальностей 190601,130602,190602

«Автомобили и автомобильное хозяйство»,

«Машины и оборудование нефтяных и газовых промыслов»

«Подъемно-транспортные, строительные, дорожные машины и оборудование»

Дневной, заочной и заочной сокращенной форм обучения

 

Сургут 2009 г.

 

Утверждено учебно-методической комиссией

государственного образовательного учреждения

высшего профессионального образования

Сургутского института нефти и газа (филиала)

Тюменского государственного нефтегазового

университета

 

Составил: доцент, канд. техн. наук Некрасов В.И.

Оформление: ст.лаборант кафедры МТО Дацюк Д.А.

 

Сургутский институт нефти и газа (филиал)

Тюменский государственный нефтегазовый университет,

2009 г.

 

 

Некрасов Владимир Иванович

 

Парный линейный

Регрессионный и корреляционный

Анализ

Экспериментальных данных

 

Методические указания

к выполнению лабораторных работ для студентов

специальностей 190601,130602,190602

 

 

Редактор

 

Подписано в печать Бумага тип №1

Формат 60 84 1/16 Усл. печ. л. Уч. изд. л.

Заказ Тираж Цена свободная

 

Издательство Тюменского государственного нефтегазового

университета.

 

Тюменский государственный нефтегазовый университет, ризограф

 

Литература

1. Айвазян С.А. Статистическое исследование зависимостей. - М.: Металлургия, 1968. - 227 с.

2. Айвазян С.А. и др. Прикладная статистика: Основы моделирования и первичная обработка данных. – М.: Финансы и статистика, 1983. – 471 с.

3. Батунер Л.М., Позин М.Е. Математические методы в химической технике. - Л.: Ленхимиздат, 1963. - 638 с.

4. Бендат Дж., Пирсол А. Прикладной анализ случайных данных: Пер. с англ. - М.: Мир, 1989. - 540 с.

5. Дьяконов В.П. Справочник по алгоритмам и программам на Бейсике для персональных ЭВМ: Справочник.- М.: Гл. ред. физ.-мат. лит., 1987. - 240 с.

6. Кассандрова О.Н., Лебедев В.В. Обработка результатов наблюдений. – М.: Наука, 1978ю – 104 с.

7. Львовский Е.Н. Статистические методы построения эмпирических формул. – М.: Высшая школа, 1982. – 224 с.

8. Мудров А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. - Томск: МП Раско, 1991. -272 с.

9. Основы научных исследований: Учеб. для техн. вузов/ 1989. – 232 с.

10. Прочность и долговечность автомобиля. – М.: Машиностроение, 1974. – 328 с.

11. Решетов Д.Н. и др. Надежность машин: Учеб. пособие для машиностр. спец. вузов. – М.: Высш. школа, 1988. – 238 с.

12. Румшиский Л.З. Математическая обработка результатов эксперимента: Справочное руководство. – М.: Наука, 1971. – 192 с.

13. Соловьев В.А., Яхонтов В.Е. Элементарные методы обработки результаты измерений. – Л.: ЛГУ, 1977. – 72 с.

14. Степнов М.Н. Статистические методы обработки результатов механических испытаний: Справочник. – М.: Машиностроение, 1985. – 232 с.

 

 

СОДЕРЖАНИЕ

 

 

ВВЕДЕНИЕ 4

1. Содержание, объем и основные правила оформления

пояснительной записки 5

Варианты заданий 9

3. Парный линейный регрессионный и корреляционный анализ

экспериментальных данных 11

3.1. Основные определения 11

3.2. Метод группировок 13

3.3. Метод средних 18

3.4. Метод наименьших квадратов 21

3.4.1. Прямая регрессия 22

3.4.2. Обратная регрессия 26

3.4.3. Корреляция 27

3.4.4. Ортогональная регрессия 28

4. Контрольные вопросы 31

ПРИЛОЖЕНИЕ 32

Литература 34

 

 

ВВЕДЕНИЕ

 

Современное производство требует от специалиста умения самостоятельно ставить и решать различные принципиально новые вопросы, чего нельзя сделать без овладения им основами научных исследований (НИ). Научная подготовка студентов в вузах – одна из важнейших сторон их обучения.

Современный специалист должен: владеть методикой НИ, их планированием и организацией, уметь отбирать и анализировать необходимую информацию, формулировать цель и задачи исследования, обосновывать теоретическую базу, планировать и проводить эксперименты, обрабатывать результаты измерений, оценивать погрешность наблюдений, сопоставлять результаты эксперимента с теоретическими предпосылками, формулировать выводы НИ, составлять отчет, доклад или статью по результатам НИ.

Цель контрольной работы – закрепить знания в области методов обработки экспериментальных данных, приобрести навыки расчетов коэффициентов регрессии и корреляции, оценивать статистическую значимость этих коэффициентов, адекватность уравнения, интерпретировать полученные результаты и т.д.

Учебные дисциплины «Методология НИОКР» и «Основы методологии научных исследований (ОМНИ)» основаны на курсе «Высшая математика» и создают основу для изучения следующих специальных дисциплин.

 

 

Таблица 2

Значение критерия Фишера при 5%-ном

уровне значимости

 

	161,45	199,50	215,71	224,58	230,16	233,99	236,77	238,88	140,54
	18,513	19,000	19,164	19,247	19,296	19,330	19,353	19,371	19,385
	10,182	9,552	9,277	9,117	9,014	8,941	8,887	8,845	8,812
	7,709	6,944	6,591	6,388	6,256	6,163	6,094	6,041	5,999
	6,608	5,786	5,410	5,192	5,050	4,950	4,876	4,818	4,773
	5,987	5,143	4,757	4,534	4,387	4,284	4,207	4,147	4,100
	5,591	4,737	4,347	4,120	3,972	3,866	3,787	3,726	3,677
	5,318	4,459	4,066	3,838	3,688	3,581	3,501	3,438	3,388
	5,117	4,257	3,863	3,633	3,482	3,374	3,293	3,230	3,179
	4,965	4,103	3,708	3,478	3,326	3,217	3,136	3,072	3,020
	4,844	3,982	3,587	3,357	3,204	3,095	3,012	2,948	2,896
	4,747	3,885	3,490	3,259	3,106	2,996	2,913	2,849	2,796
	4,667	3,806	3,411	3,179	3,025	2,915	2,832	2,767	2,714
	4,600	3,739	3,344	3,112	2,958	2,848	2,764	2,699	2,646
	4,543	3,682	3,297	3,056	2,901	2,791	2,707	2,641	2,588
	4,494	3,634	3,239	3,007	2,852	2,741	2,657	2,591	2,538
	4,451	3,592	3,197	2,965	2,810	2,699	2,614	2,548	2,494
	4,414	3,555	3,160	2,928	2,773	2,661	2,577	2,510	2,456
	4,381	3,522	3,127	2,895	2,740	2,628	2,544	2,477	2,423
	4,351	3,493	3,098	2,866	2,711	2,599	2,514	2,447	2,393
	4,325	3,467	3,073	2,840	2,685	2,573	2,488	2,421	2,366
	4,301	3,443	3,049	2,817	2,661	2,549	2,464	2,397	2,342
	4,279	3,422	3,028	2,796	2,640	2,528	2,442	2,375	2,320
	4,260	3,403	3,009	2,776	2,621	2,508	2,423	2,355	2,300
	4,242	3,385	2,991	2,759	2,603	2,490	2,405	2,337	2,282
	4,225	3,369	3,975	2,743	2,587	2,474	2,388	2,321	2,266
	4,210	3,354	2,960	2,728	2,572	2,459	2,373	2,305	2,250
	4,196	3,340	2,947	2,714	2,558	2,445	2,359	2,291	2,236
	4,183	3,328	2,934	2,701	2,545	2,432	2,346	2,278	2,223
	4,171	3,316	2,922	2,690	2,534	2,421	2,334	2,266	2,211
	4,085	3,232	2,839	2,606	2,450	2,336	2,249	2,180	2,124
	4,001	3,150	2,758	2,525	2,368	2,254	2,167	2,097	2,040
	3,920	3,072	2,680	2,447	2,290	2,175	2,087	2,016	1,959
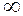
	3,842	2,996	2,605	2,372	2,214	2,099	2,010	1,938	1,880

 

ПРИЛОЖЕНИЕ

Таблица 1

Распределение Стьюдента t=t(P; k)

P k	0,90	0,95	0,98	0,99	0,999
	2,132	2,776	3,747	4,604	8,610
	2,015	2,571	3,365	4,032	6,859
	1,943	2,447	3,143	3,707	5,959
	1,895	2,365	2,998	3,499	5,405
	1,860	2,306	2,896	3,355	5,041
	1,833	2,262	2,821	3,250	4,781
	1,812	2,228	2,764	3,169	4,587
	1,796	2,201	2,718	3,106	4,487
	1,782	2,179	2,681	3,055	4,318
	1,771	2,160	2,650	3,012	4,221
	1,761	2,145	2,624	2,977	4,140
	1,753	2,131	2,602	2,947	4,073
	1,746	2,120	2,583	2,921	4,015
	1,734	2,103	2,552	2,878	3,922
	1,725	2,086	2,528	2,845	3,850
	1,708	2,060	2,485	2,787	3,725
	1,697	2,042	2,457	2,750	3,646
	1,689	2,030	2,437	2,724	3,591
	1,684	2,021	2,423	2,704	3,551
	1,679	2,014	2,412	2,689	3,522
	1,676	2,008	2,403	2,677	3,497
	1,671	2,000	2,390	2,660	3,460
	1,667	1,995	2,381	2,648	3,436
	1,664	1,990	2,374	3,639	3,416
	1,662	1,987	2,368	2,632	3,401
	1,660	1,984	2,364	2,626	3,391
	1,645	1,960	2,326	2,576	3,291

 

СОДЕРЖАНИЕ, ОБЪЕМ И ОСНОВНЫЕ ПРАВИЛА ОФОРМЛЕНИЯ ПОЯСНИТЕЛЬНОЙ ЗАПИСКИ

 

Контрольная работа состоит из пояснительной записки.

Пояснительная записка (ПЗ) является техническим отчетом и должна быть выполнена в соответствии с требованиями ГОСТ 72-91 и ГОСТ 2 105-95.

ПЗ должна содержать титульный лист, оглавление, введение, основную часть, заключение и список источников (литературы), использованных при выполнении работы.

Содержание и объем работ могут быть изменены по согласованию с кафедрой МТО.

Титульный лист должен иметь: полное название высшего учебного заведения, кафедры, учебной дисциплины, по которой выполнена работа, название (тему) работы, номер её варианта; фамилию, инициалы и подпись исполнителя работы с указанием номера студенческой группы и формы обучения; должность, ученую степень, научное звание, фамилию и инициалы преподавателя; место и год выполнения работы.

Оглавление (содержание) должно содержать перечень структурных элементов работы с указанием номеров страниц, с которых начинается их месторасположение в тексте, в том числе включает: введение, наименования всех разделов и подразделов и пунктов (если они имеют наименования), заключение, список источников. Нумеруется только основная часть работы; введение, заключение и источники не нумеруются.

Введение размером не более 1 стр. должно отражать актуальность темы и цель работы.

ПЗ к контрольной работе должна содержать основную часть объемом не менее 10 страниц. Помимо текста должны быть рисунки, таблицы. Общий объем ПЗ не менее 15 страниц.

ПЗ выполняется в текстовом режиме Word шрифтом Times New Roman N 14 на светлой (белой) бумаге и брошюруется в папку формата А4 (297х210 мм). При заполнении листов только с одной стороны текст следует оформлять с соблюдением следующих размеров полей: левое – 25 мм, правое – 10 мм, верхнее и нижнее – 20 мм.

При этом рамки и штампы на листах формата А4 не выполняются.

Абзацы в тексте начинают с отступом в 15…18 мм (5 знаков).

При оформлении ПЗ машинописным способом текст должен быть отпечатан через полтора межстрочных интервала, в том числе с применением печатающих и графических устройств вывода ЭВМ. Допускается печатать записку через два межстрочных интервала. Минимальная высота шрифта 2,5 мм. Шрифт машинки должен быть четким, лента четного цвета средней жирности. Плотность текста должна быть одинаковой.

Страницы нумеруют арабскими цифрами. Титульный лист включают в общую нумерацию. На титульном листе номер не ставят, на последующих станицах номер проставляют по центру в нижней части листа в соответствии с требованиями к оформлению дипломных проектов.

Текст записки должен быть четким, ясным, без грамматических ошибок и не допускать различных толкований. Сокращения русских слов и словосочетаний допускается только в соответствии с ГОСТ 7.12-77. Текст документа при необходимости разделяют на разделы, подразделы, пункты и подпункты. Каждый раздел следует начинать с нового листа, подразделы – по тексту.

Заголовки располагают по центру листа. Заголовки разделов оформляют прописными (заглавными) буквами одинаковой высоты жирным шрифтом № 16.

Заголовки подразделов – строчными буквами (кроме первой прописной) жирным шрифтом № 14.

Переносы слов в заголовках не допускаются. Точку в конце заголовка не ставят. Если заголовок состоит из двух предложений, то их разделяют точкой.

Все заголовки, кроме введения и заключения, нумеруются арабскими цифрами. Подразделы и параграфы (пункты) нумеруются соответственно двумя или тремя цифрами, разделенными точкой.

Расстояние между текстом и заголовком должно быть равно 3…4 интервалам (не менее 15 мм). Подчеркивать заголовки не допускается.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Цель регрессионного анализа?

2. Цель корреляционного анализа?

3. Как взаимосвязаны регрессия и корреляция?

4. Суть метода наименьших квадратов?

5. Чем отличаются прямая и обратная регрессии?

6. Чему равен коэффициент корреляции в случае функциональной зависимости?

7. В какой точке пересекаются линии прямой и обратной регрессии?

8. Чем отличаются остаточная дисперсия и общая дисперсия?

9. Как проверяется значимость коэффициентов регрессии и корреляции?

10. Как оценивается адекватность уравнения?

11. Объясните физический смысл коэффициентов регрессии.

12. Чему равен коэффициент парной корреляции, если линии прямой и обратной регрессии перпендикулярны?

13. Как направлена линия регрессии при

?

14. Как направлена линия регрессии при

?

15. Как направлена линия обратной регрессии при

?

16. Как направлена линия обратной регрессии при

?

17. Сколько линий на графике парной зависимости при ?

18. Как взаимосвязаны доверительные границы и доверительные интервалы?

19. Критерий Фишера, его назначение и применение?

20. Критерий Стъюдента, его назначение и применение?

21. Число степеней свободы, где и как применяется?

 

 

8. Из уравнения обратной регрессии с новыми коэффициентами

 

= b_{0 (ху)}’ + b_{1 (ху)} ’ определяем свободный член уравнения ортогональной регрессии относительно оси ординат

b_{0 (ху)}’ = - b_{1 (ху)}’ = 7,44 – 1,6355×7,69 = -5,137.

9. Записываем уравнение ортогональной регрессии относительно оси ординат

Х_ort = b_{0 (ху)}’ + b_{1 (ху)}’Y = -5,137 + 1,6355 Y.

10. Производим вычисления, аналогичные ранее выполненным, и заполняем таблицу 2

X_ort1 = -5,14 + 1,64×5,0 = 3,06;

x₁ = 1,5 – 3,06 = - 1,56; x₁² = 2,4336;

X _{ort 2} = -5,14 + 1,64×4,5 = 2,24 и т.д.;

11. Определяем абсолютные отклонения экспериментальных значений перпендикулярно линии ортогональной регрессии и квадраты этих отклонений. Абсолютные отклонения Y₁ = 0,945 и X₁ = -1,56 являются катетами прямоугольного треугольника.

tg α = 0,945/1,56 = 0,606; α = 31,21⁰; sin 31,21⁰ = 0,518; h₁ = 0,518×1,56 = 0,808; h₁² = 0,653 и т.д.

Результаты вычислений заносим в таблицу 2.

Оптимальным считается вариант, при котором сумма квадратов отклонений от экспериментальных точек до проведенной линии регрессии была бы минимальной.

Анализ результатов вычислений в таблице 2 показывает, что лучшей является ортогональная регрессия, для которой сумма квадратов отклонений составляет 6,86.

Лабораторная работа оценивается преподавателем по аккуратно оформленному студентом отчету с результатами статистической обработки и по ответам на контрольные вопросы по данной теме.

Иллюстрации (рисунки, графики, схемы, диаграммы, фотоснимки и т.д.) помещают непосредственно за ссылкой в тексте на этот рисунок или на следующей странице, если на предыдущей странице, которая должна быть полностью заполнена, для рисунка места недостаточно. В тексте ПЗ должны быть ссылки на все иллюстрации.

Иллюстрации должны иметь название, которое помещают под иллюстрацией центрированным способом без подчеркиваний и точки в конце. Рисунок должен иметь номер и, по необходимости, подрисуночный текст. Рисунки нумеруют в пределах раздела. При небольшом объёме записки допускается сплошная нумерация рисунков. Поясняющие надписи выполняют через один интервал шрифтом № 12 и помещают за подрисуночной надписью или справа от рисунка. Иллюстрации отделяют от текста свободной строкой сверху и снизу.

Все формулы записываются отдельной строкой с абзаца с интервалом 7…10 мм от предыдущего и последующего текста. Значения символов и числовых коэффициентов, входящих в формулу, должны быть раскрыты по тексту перед формулой или перечислены непосредственно после нее. Перечисление символов после формулы должно начинаться со слова “где”. В этом перечислении могут быть приведены значения величин с указанием единиц измерения.

После формулы обязательно должен быть приведен пример расчета с постановкой числовых значений в соответствии с символами. Для результата расчета по формуле единицы измерения (в системе СИ) указываются обязательно.

При большом объеме однотипных вычислений их сводят в таблицы.

Таблицы в ПЗ располагают, аналогично иллюстрациям, непосредственно после текста, в котором они упоминаются впервые, или на следующей странице, отделяя от текста сверху и снизу свободной строкой. В тексте ПЗ должны быть ссылки на все таблицы. Таблица обязательно должна иметь заголовок по центру без подчеркивания, точку в конце заголовка не ставят.

Таблицы нумеруют арабскими цифрами с указанием порядкового номера раздела и номера таблицы в этом разделе.

Номер размещают в правом верхнем углу над заголовком таблицы после слова «Таблица». Например, Таблица 1.2. – вторая таблица первого раздела. Если в ПЗ одна таблица, то ее не нумеруют и слово «Таблица» не пишут.

При переносе таблицы на следующей странице повторяют «шапку» таблицы и над ней указывают «Продолжение». Например, «Продолжение табл. 1.2.».

Список литературы и других источников информации, использованных при написании контрольной работы, должен быть помещен в конце ПЗ.

Формулы, знаки, отдельные слова допускается вписывать в отпечатанный текст только черными чернилами или тушью.

Опечатки и графические неточности допускается исправлять подчисткой или закрашиванием «штрихом» и нанесением на том же месте исправленного изображения.

 

 

2. Определяем угол между линиями прямой и обратной регрессии

γ = 90⁰ – (27,92⁰ + 55,035⁰) = 7,045⁰.

3. Определяем угол наклона и угловой коэффициент линии ортогональной регрессии относительно оси абсцисс– (прямая регрессия)

α^' = α + γ /2 = 27,92⁰ + 7,045⁰/2 = 31,4425⁰; b_1(yх)’ = tg α ^' = 0,6114.

4. Определяем угол наклона и угловой коэффициент линии ортогональной регрессии относительно оси ординат– (обратная регрессия)

β' = β + γ /2 = 55,035⁰ + 7,045⁰/2 = 58,5575⁰; b_1(xy)’ = tg β’ = 1,6355.

Проверка: α^' + β' = 31,4425⁰ + 58,5575⁰ = 90⁰;

tg α ^' х tg β’ = 0,6114х1,6355 = 1,0.

5. Из уравнения прямой регрессии с новыми коэффициентами

= b_{0 (ух)}’ + b_{1 (ух)}’ определяем свободный член уравнения ортогональной регрессии относительно оси абсцисс

b_{0 (ух)}’= - b_{1 (ух)}’ = 7,69 – 0,6114×7,44 = 3,141.

6. Записываем уравнение ортогональной регрессии относительно оси абсцисс и наносим линию на график (рис. 2)

У_ort = b_{0 (ух)}’ + b_{1 (ух)}’X = 3,141 + 0,6114 Х.

7. Производим вычисления, аналогичные ранее выполненным, и заполняем таблицу 2

У_{ort 1} = 3,14 + 0,61×1,5 = 4,055:

Y₁ = У_{1 эк} - У_ort1 = 5,0 – 4,055 = 0,945; Y₁² = 0,8930;

У_ort2 = 3,14 + 0,61 × 4,0 = 5,58;

Y₂ = У_{2 эк} - У_ort2 = 4,5 – 5,58 = -1,08; Y₂² = 1,1664 и т.д.

3. Проверяем статистическую значимость коэффициента парной корреляции

.

Коэффициент корреляции r = 0,873 находится на высоком уровне и статистически значим.

Ортогональная регрессия

При коэффициенте корреляции, приближающемся к единице, расчеты по уравнениям прямой и обратной регрессии дают достаточно близкие результаты. Чем меньше по абсолютной величине коэффициент корреляции, тем больше угол между линиями прямой и обратной регрессии и выше различие между результатами, полученными по двум уравнениям. При этом искажается физический смысл полученных зависимостей. Целесообразно иметь одно уравнение, описывающее взаимозависимость между исследуемыми величинами.

Ортогональная регрессия дает одно уравнение на основе уравнений прямой и обратной регрессии. Линия ортогональной регрессии должна быть биссектрисой - делить пополам угол между линиями прямой и обратной регрессии.

1. Определяем углы наклона линий регрессии к осям координат

b_1(yх) = tg α = 0,5326, угол α = 27,92⁰; b_1(xy) = tg β = 1,4294, угол β = 55,035⁰;

где b_1(yх) – угловой коэффициент уравнения прямой регрессии - тангенс угла наклона линии прямой регрессии к оси абсцисс, b_1(xy) - угловой коэффициент уравнения обратной регрессии - тангенс угла наклона линии обратной регрессии к оси ординат.

 

ВАРИАНТЫ ЗАДАНИЙ

 

Исходные данные для контрольной работы выбирают из таблицы 1. В верхней строке приведены координаты точек по оси абсцисс (Х) от -6 до 13. В следующих строках – координаты точек по оси ординат (У). Для статистической обработки надо выбрать 10 точек.

Номер варианта контрольной работы определяется по номеру студента в списке группы. Возможно изменение темы контрольной работы по согласованию с преподавателем данной дисциплины.

Например, для 1-го варианта: Х₁ = -5, У₁ = 1; Х₂ = -3, У₂ = 2; Х₃ = -1, У₃ = 4; Х₄ = 1, У₄ = 3; Х₅ = 3, У₅ = 5; Х₆ = 5, У₆ = 4; Х₇ = 7, У₇ = 6; Х₈ = 9, У₈ = 5; Х₉ = 11, У₉ = 7; Х₁₀ = 13, У₁₀ = 7.

Таблица 1

Исходные данные

 

№ варианта	Верхняя строка – ось абсцисс – х, далее строки – ось ординат - у
-6	-5	-4	-3	-2	-1
																-3		-3		-5
															-4		-4		-6
	-12		-10		-7		-8		-5		-1
		-12		-10		-7		-8		-5		-1
							-1				-2		-3		-2		-4		-5
												-1		-2		-1		-3		-4

Продолжение табл.1.

 

№ варианта	Верхняя строка – ось абсцисс – х, далее строки – ось ординат - у
-6	-5	-4	-3	-2	-1
															-1		-4		-6
																-2		-5		-7
															-1	-2	-4	-4	-6	-7
	-6		-5		-5		-4		-3		-3		-2		-1
		-6		-5		-4		-4		-3		-2		-2		-1
	-6	-6	-5	-5	-5	-4	-4	-4	-3	-3
											-3	-2	-2	-2	-1	-1
	-14		-12		-11		-10		-9		-8		-6		-5		-4		-3
		-13		-12		-11		-9		-8		-7		-6		-4		-3		-2
	-14	-13	-12	-12	-11	-11	-10	-9	-9	-8
											-8	-7	-6	-6	-5	-4	-4	-3	-3	-2

 

 

2. Выполняем вычисления аналогичные прямой регрессии. Коэффициенты уравнения обратной регрессии статистически значимы. Получили уравнение обратной регрессии

X = b_{0 (ху)} + b_{1 (ху)} У = -3,55 + 1,43 У.

X_1р = -3,55 + 1,43 х5,0 = 3,6;

X₁ = 1,5 – 3,6 = - 2,1; X₁² = 4,41;

X_2р = -3,55 + 1,43 х4,5 = 2,855 и т.д.;

3. Наносим линию обратной регрессии на график (рис. 2), указываем на графике величины коэффициентов обратной регрессии. Линия обратной регрессии круче линии прямой регрессии, обе линии пересекаются в центре массива экспериментальных данных = 7,44 и = 7,69.

 

Корреляция

1. Вычисляем коэффициент парной корреляции

 

=

 

Проверка r = Q_ху / (Q_х Q_у)^0,5 = 52,84/(99,22х36,97)^0,5 = 0,87.

2. Проверяем правильность вычислен

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: