Получим частотную передаточную функцию в виде

Для наглядного представления частотных свойств динамических звеньев используются так называемые частотные характеристики: во-первых, амплитудная частотная характеристика (АЧХ), которая определяет зависимость амплитуды выходного сигнала от частоты колебаний при постоянстве амплитуды входного сигнала (рис. 2.3, а); во-вторых, фазовая частотная характеристика (ФЧХ), показывающая фазовые сдвиги, вносимые звеном на разных частотах (рис. 2.3, б); в-третьих, амплитудно-фазовая частотная характеристика '(АФЧХ), которая объединяет амплитудную и фазовую частотные характеристики при использовании их в качестве полярных координат (рис. 2.3, в), Каждая точка АФЧХ соответствует определенному значению частоты ω. Эту характеристику можно построить и в прямоугольной системе координат — в комплексной плоскости. При этом координатами будут показанные на рис. 2.3, в проекции Р и Q вектора А на соответствующие оси.

Иногда строятся также вещественная Р() и мнимая Р(со) частотные характеристики (рис. 2.4).

Согласно формулам (2.6) и (2.7) связь между названными частотными характеристиками определяется следующими выражениями:

 

 

При исследовании САУ амплитудную и фазовую частотные характеристики удобно строить в логарифмических координатах. Это даёт возможность очень просто построить логарифмические частотные характеристики (ЛЧХ) даже для сложных устройств. Прологарифмируем выражение частотной передаточной функции (2.6)

Ln W(jω) = ln A(ω)+jφ(ω)

Из этого выражения видно, что член ln A(ω) определяет логарифмическую амплитудную частотную характеристику (ЛАХ), а φ (ω) – логарифмическую фазовую частотную характеристику (ЛФК).

Построение ЛАЧХ и ЛФЧХ систем и звеньев производится в прямоугольной системе координат. Координатные оси представляются в виде шкал, позволяющих произвести разметку осей в определенных единицах измерения. Подготовку системы координат для построения ЛЧХ рассмотрим подробнее.

Ось абсцисс

Ось абсцисс называется осью частот. На ней откладываются десятичные логарифмы частоты и значения самой частоты в логарифмическом масштабе. В отношении ln ω шкала частот получается линейной, а в отношении частоты ω — логарифмической. Основными единицами измерения по оси частот являются декада и октава.

Декадой называется интервал частот, различающихся между собой в 10 раз.

Октавой называется интервал частот, различающихся между собой в 2 раза.

На шкале частот, построенной в логарифмическом масштабе, длина отрезка, представляющего декаду (октаву), остается одной и той же на любом участке оси частот.

Масштаб декады выбирается с точки зрения удобства построения и допустимой относительной погрешности построения. Общепринятым является масштаб

т = 50 мм. (3.5.5)

Расчетные данные для изготовления линейки-шаблона с этим масштабом приведены в табл. 3.5.1. После того, как построена одна декада, остальные декады на шкале частот получаются простым ее повторением.

Таблица 3.5.1

ω					5
lg ω		0,3	0,48	0,6	0,7	0,78	0,85	0,9	0,95
l							42,5		47,5

Логарифмическая шкала на оси частот не имеет точки с отметкой ω = 0(1^0 = °°). Это позволяет ось ординат проводить через начало любой декады (октавы), что весьма удобно при построении ЛЧХ.

Ось ординат

Эта ось называется осью усиления. При построении ЛАЧХ системы или звена за единицу измерения по оси ординат принимается децибел, при построении ЛФЧХ —градус, при этом применяются следующие масштабы:

I дб = 2 мм, 1 Г = 1 мм. (3.5.6)

С соблюдением этих масштабов и производится разметка оси усиления в указанных единицах измерения.

Децибел — логарифмическая единица для оценки отношения двух величин- Значение какой-либо положительной величины в децибелах численно равно десятичному логарифму этой величины, увеличенному в 20 раз. Например, значение общего коэффициента усиления системы K в децибелах определится по формуле

Кдб = 20 lg K(3.5,7)

Типовая логарифмическая сетка для построения ЛАЧХ и ЛФЧХ с масштабами (3.5.5) и (3.5.6) по осям координат изображена на рис. 3.5.1.

 

 

Основные характеристики звеньев и систем.

 

При синтезе и анализе САУ ее расчленяют на типовые звенья, которые различаются динамическими свойствами.

Характеристики типовых звеньев.

За типовые звенья, по-видимому, целесообразно принять такие, которые могут служить основой для построения любых других звеньев, встречающихся на практике. Обычно за основу принимают звено, обладающее одной степенью свободы. Математические процессы в таком звене описываются дифференциальным уравнением не выше второго порядка

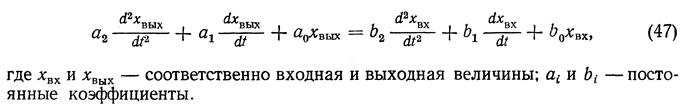
В основу классификации звеньев кладётся вид дифференциального уравнения, которым могут описываться весьма разнообразные свойства как по своей функции, так и по своему конструктивному исполнению.

Если принять это уравнение за исходное, то легко вывести уравнения различных типовых звеньев.

Типовые звенья являются звеньями направленного действия: сигналы передаются звеном в одном направлении — со входа на выход.

Типовые звенья подразделяют на пропорциональные (усилительные), апериодические (инерционные), колебательные, интегрирующие, дифференцирующие и форсирующие. Несколько обособленно в этой классификации стоит запаздывающее звено.

 

Дифференциальные уравнения и основные характеристики типовых звеньев, рассмотренные далее, приведены в табл. 1.

 

 

 

Из рассмотренных типовых звеньев элементарными явля­ются пропорциональное, интегрирующее и дифференцирующее. Все другие звенья можно сформировать из элементарных пу­тем соответствующего соединения их между собой.

Звенья, у которых переходная функция со временем зату­хает, называются устойчивыми. Типовые звенья всегда устой­чивы. Их действие описывается линейными дифференциальны­ми уравнениями с положительными коэффициентами. Исклю­чение составляет интегрирующее звено, которое исходя из усло­вий устойчивости, называют нейтральным. В неустойчивых: звеньях переходный процесс является расходящимся. Действие этих звеньев описывается линейными дифференциальными урав­нениями с отрицательными коэффициентами.

 

Следует заметить, что в зависимости от сигналов, приняты за входной и выходной, а также от принятых при составлении дифференциальных уравнений допущений один и тот же элемент САУ можно описать разными уравнениями, а значит, отобразить различными типовыми звеньями. Например, если для электродвигателя постоянного тока (рис. 2.14) за входной сигнал принято напряжение на якоре и_я {и_во3(> — напряжение возбуждения двигателя), а за выходной — угол поворота а вы­ходного вала и если такой электродвигатель считать безынер­ционным, то он будет отображен интегрирующим звеном:

Если для этого же электродвигателя за выходной сигнал при­нять скорость вращения Q = a, то он будет уже представлен безынерционным (пропорциональным) звеном:

Если же при тех же входных и выходных сигналах учесть инерционность электродвигателя, то он должен быть отобра­жен либо двумя последовательно включенными звеньями — ин­тегрирующим и апериодическим:

либо одним апериодическим звеном:

 

 

В зависимости от сложности дифференциального уравнения элемента САУ последний может быть представлен одним или несколькими типовыми звеньями, определенным образом соеди­ненными между собой.

 

 

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: