 |
Типовой расчет по линейной алгебре
|
|
|
|
Вариант 5
- Найти произведение матриц АВ, если

- Найти ранг матрицы
 .
.
- Матричным методом и по правилу Крамера найти решение системы уравнений

- Методом Гаусса-Жордана найти решение системы уравнений

5. Дано:  4,
4,  6, угол j между векторами
6, угол j между векторами 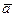 и
и  равен
равен  .
.
а) Найти угол между векторами  и
и 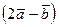 .
.
б) Найти площадь параллелограмма, построенного на векторах  и
и 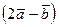 .
.
6. Найти вектор 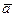 , если он перпендикулярен векторам
, если он перпендикулярен векторам  ,
,  и удовлетворяет условию
и удовлетворяет условию  5, где
5, где  .
.
7. Средствами векторной алгебры найти точку пересечения прямой, проходящей через точки  и
и 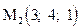 , с плоскостью Oyz.
, с плоскостью Oyz.
8. Средствами векторной алгебры найти точку пересечения плоскости, проходящей через точки А(4; 1; 1), В(2; 1; 5), С(4; 5; 3) с осью O z.
9. Даны координаты вершин пирамиды:  . Требуется средствами векторной алгебры найти:
. Требуется средствами векторной алгебры найти:
а) угол между ребрами 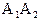 и
и  ;
;
б) площадь грани  ;
;
в) проекцию вектора 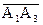 на вектор
на вектор  ;
;
г) объем пирамиды.
10. Даны вершины треугольника А-4; 3), В(4; -1) и точка пересечения высот М(3; 4). Найти уравнение стороны ВС.
11. Составить уравнения сторон треугольника, если даны одна из его вершин А(2; 3) и уравнения медианы  и высоты
и высоты  , проведенных из разных вершин.
, проведенных из разных вершин.
12. Найти уравнение прямой, проходящей через точку М(3; 5) и правый фокус гиперболы  . Сделать чертеж.
. Сделать чертеж.
Типовой расчет по линейной алгебре
Вариант 6
1.Найти произведение матриц АВ, если

2.Найти ранг матрицы
 .
.
3.Матричным методом и по правилу Крамера найти решение системы уравнений

4.Методом Гаусса-Жордана найти решение системы уравнений

5. Дано:  4,
4,  6, угол j между векторами
6, угол j между векторами 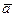 и
и  равен
равен  .
.
а) Найти угол между векторами  и
и 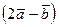 .
.
б) Найти площадь параллелограмма, построенного на векторах  и
и 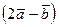 .
.
6. Найти вектор 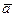 , если он перпендикулярен векторам
, если он перпендикулярен векторам  ,
, 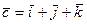 и удовлетворяет условию
и удовлетворяет условию  6, где
6, где  .
.
|
|
|
7. Средствами векторной алгебры найти точку пересечения прямой, проходящей через точки  и
и 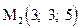 , с плоскостью Oxy.
, с плоскостью Oxy.
8. Средствами векторной алгебры найти точку пересечения плоскости, проходящей через точки А(5; 1; 2), В(4; 2; 5), С(3;3; 5) с осью O x.
9. Даны координаты вершин пирамиды:  . Требуется средствами векторной алгебры найти:
. Требуется средствами векторной алгебры найти:
а) угол между ребрами 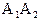 и
и  ;
;
б) площадь грани  ;
;
в) проекцию вектора 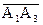 на вектор
на вектор  ;
;
г) объем пирамиды.
10. Даны вершины треугольника А(2; 5) и В(5; 3) параллелограмма ABCD и точка М(-2; 0) пересечения его диагоналей. Составить уравнения сторон этого параллелограмма.
11. Составить уравнения сторон треугольника, если даны одна из его вершин А(2; 3) и уравнения высоты  и биссектрисы
и биссектрисы  , проведенных из разных вершин.
, проведенных из разных вершин.
12. Найти расстояние от точки А(1; 2) до фокуса параболы 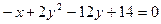 .
.
Сделать чертеж.
Типовой расчет по линейной алгебре
Вариант 7
- Найти произведение матриц АВ, если

- Найти ранг матрицы
 .
.
- Матричным методом и по правилу Крамера найти решение системы уравнений

- Методом Гаусса-Жордана найти решение системы уравнений

5.Дано:  4,
4,  6, угол j между векторами
6, угол j между векторами 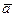 и
и  равен
равен  .
.
а) Найти угол между векторами  и
и  .
.
б) Найти площадь параллелограмма, построенного на векторах  и
и 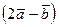 .
.
6. Найти вектор 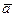 , если он перпендикулярен векторам
, если он перпендикулярен векторам  ,
,  и удовлетворяет условию
и удовлетворяет условию  2, где
2, где  .
.
7. Средствами векторной алгебры найти точку пересечения прямой, проходящей через точки  и
и 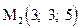 , с плоскостью Oxz.
, с плоскостью Oxz.
8. Средствами векторной алгебры найти точку пересечения плоскости, проходящей через точки А(5; 1; 2), В(4; 2; 5), С(3; 3; 5) с осью O y.
9. Даны координаты вершин пирамиды:  . Требуется средствами векторной алгебры найти:
. Требуется средствами векторной алгебры найти:
а) угол между ребрами 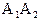 и
и  ;
;
б) площадь грани  ;
;
в) проекцию вектора 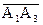 на вектор
на вектор  ;
;
г) объем пирамиды.
10. Центр симметрии квадрата находится в точке (-1; 0), уравнение одной его стороны 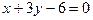 . Составить уравнения остальных сторон квадрата.
. Составить уравнения остальных сторон квадрата.
|
|
|
11. Составить уравнения сторон треугольника, если даны одна из его вершин А(2; 3) и уравнения биссектрисы  и высоты
и высоты  , проведенных из разных вершин.
, проведенных из разных вершин.
12. Найти уравнения асимптот и эксцентриситет гиперболы  .
.
Сделать чертеж.
|
|
|


