 |
Кинетика и динамика сорбции из водных растворов
|
|
|
|
Движущей силой процесса сорбции из водных растворов является градиент химического потенциала сорбата. По достижении равенства химических потенциалов последнего в объеме раствора и в сорбенте наступает химическое равновесие. Лимитирующее влияние на скорость сорбции оказывают подвод сорбируемого вещества к зерну сорбента (внешний массоперенос) и перемещение его молекул внутри зерна пористого сорбента (внутренняя диффузия). Обычно во всех аппаратах и сооружениях сорбционной очистки воды путем турбулизации потоков и интенсивного подвода новых порций воды снимаются внешнедиффузионные ограничения, а единственной стадией, лимитирующей кинетику, является перенос вещества в транспортных порах, равномерно распределенных по всему объему зерна сорбента. Собственно акт сорбции – заполнение микропор – происходит столь быстро, что не влияет на кинетику процесса в целом.
Диффузия в транспортных порах (мезо- и макропорах) прямо пропорциональна градиенту концентраций. Скорость сорбции, при прочих равных условиях, убывает с ростом размеров зерна сорбента  и уменьшением объемов транспортных пор, что и подтверждено экспериментально. Скорость сорбции (dC / d τ) обратно пропорциональна
и уменьшением объемов транспортных пор, что и подтверждено экспериментально. Скорость сорбции (dC / d τ) обратно пропорциональна  .
.
При контакте сорбента с раствором в первый момент времени (τк < 10 мин), необходимый для заполнения пор сорбента раствором, кинетика сорбции зависит от интенсивности внешнего массопереноса. Затем лимитирующей стадией становится внутренняя диффузия, и скорость сорбции выражается зависимостью:
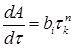 (33)
(33)
где bi – константа, а n обычно равно 0,5.
Скорость сорбции зависит от отличия степени насыщения сорбента  в данный момент и равновесной
в данный момент и равновесной  . Это нашло отражение в формуле, предложенной Родзиллером
. Это нашло отражение в формуле, предложенной Родзиллером
|
|
|
 (34)
(34)
и в уравнении Глюкауфа
 (35)
(35)
где 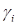 – константа;
– константа;  – концентрация вещества в растворе.
– концентрация вещества в растворе.
Скорость изменения химического потенциала (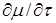 ) предложено определять по формуле
) предложено определять по формуле
 (36)
(36)
где  – кинетическаий параметр;
– кинетическаий параметр; 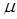 и
и  – текущее и равновесное значения химического потенциала;
– текущее и равновесное значения химического потенциала;
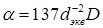 (динамические условия) (37)
(динамические условия) (37)
 (статические условия)
(статические условия)
где  – эффективный коэффициент диффузии, зависящий от ряда параметров.
– эффективный коэффициент диффузии, зависящий от ряда параметров.
На скорость сорбции могут оказывать влияние примеси в сорбенте. Так, наличие металлов на поверхности АУ, не увеличивая 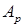 , приводит к росту
, приводит к росту  .
.
Изучение динамики сорбции позволяет найти основные расчетные параметры систем сорбционной очистки воды: эффективность; длину зоны массопередачи и скорость ее движения; время работы адсорберов.
Классическое уравнение динамики сорбции, до сих пор использующееся для расчетов, было предложена Шиловым:
 или
или  (38)
(38)
Здесь  – время до «проскока» – время защитного действия адсорбера;
– время до «проскока» – время защитного действия адсорбера;  – высота адсорбера;
– высота адсорбера;  и
и  – константы:
– константы:  характеризует пространство и время, необходимое для формирования и проведения собственно массообменного процесса;
характеризует пространство и время, необходимое для формирования и проведения собственно массообменного процесса;  – коэффициент защитного действия;
– коэффициент защитного действия;  – мертвый слой;
– мертвый слой;  – скорость потока жидкости;
– скорость потока жидкости;  – предельная динамическая емкость сорбента при данной исходной концентрации
– предельная динамическая емкость сорбента при данной исходной концентрации  .
.
Один из подходов к решению задачи динамики сорбции, реализованный Родзиллером, базируется на уравнении материального баланса веществ
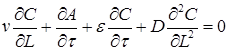 (39)
(39)
где  – порозность слоя сорбента;
– порозность слоя сорбента;  – длина (высота) адсорбера.
– длина (высота) адсорбера.
Первый член уравнения (39) отражает количество загрязнений, поступающих в адсорбер, второй – задержанных загрязнений, третий – остаток загрязнений в воде, четвертый (практически равен нулю в адсорбере с плотным слоем) – продольную диффузию. Решение (39) совместно с (38) позволяет получить выражение для определения эффекта очистки воды (С/С0):
|
|
|
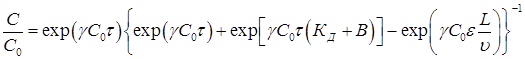 (40)
(40)
где  – коэффициент;
– коэффициент;  – динамическая константа равновесия в первом приближении, равная
– динамическая константа равновесия в первом приближении, равная 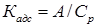 ;
;  – время контакта воды и адсорбента.
– время контакта воды и адсорбента.
Если используется высокоэффективный адсорбент, изымающий все примеси из воды, тогда член  в уравнении (39) и уравнении (40) примет вид:
в уравнении (39) и уравнении (40) примет вид:
 (41)
(41)
Приведенные уравнения с учетом различия  позволяют решить задачу перехода от экспериментальных установок к промышленным. На коэффициент
позволяют решить задачу перехода от экспериментальных установок к промышленным. На коэффициент  оказывают влияние природа сорбата и сорбента, пористость сорбента и степень заполнения его пор. При очистке многокомпонентных растворов (реальных вод) ожидается снижения
оказывают влияние природа сорбата и сорбента, пористость сорбента и степень заполнения его пор. При очистке многокомпонентных растворов (реальных вод) ожидается снижения  при увеличении
при увеличении  (продвижение потока воды через адсорбер) вследствие хроматографического эффекта. Эксперименты показали, что при
(продвижение потока воды через адсорбер) вследствие хроматографического эффекта. Эксперименты показали, что при  мг/дм3 и
мг/дм3 и  м/ч значения
м/ч значения  изменяются:
изменяются:  при
при  и
и  м, а при
м, а при  и
и  и
и  , т.е.
, т.е.  монотонно убывает при увеличении
монотонно убывает при увеличении  и
и  . Чем ниже концентрация примесей в воде, тем вероятнее попадание в очищенную воду только трудносорбируемых компонентов.
. Чем ниже концентрация примесей в воде, тем вероятнее попадание в очищенную воду только трудносорбируемых компонентов.
Для случая сорбции индивидуальных загрязнений Стадником предложены формулы для расчета основных параметров:
τпр – время работы адсорбера с плотным слоем до проскока;
Δτ – время от начала проскока до полной отработки слоя сорбента;
L мп – длины зоны массопередачи (при известном эффективном коэффициента диффузии D, выпуклой изотерме адсорбции и L ≥ L мп):
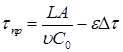 (42)
(42)
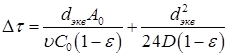 (43)
(43)
 (44)
(44)
Здесь  – фиктивная скорость фильтрования; А0 – равновесная динамическая емкость сорбента при С0; ε – порозность слоя адсорбента.
– фиктивная скорость фильтрования; А0 – равновесная динамическая емкость сорбента при С0; ε – порозность слоя адсорбента.
Неизвестные величины А0 и D (или d экв / D) можно найти несколькими способами. Во-первых, можно экспериментально получить изотерму и выходную кривую динамики сорбции (при любых d экв) и найти А0 и τпр, а затем перейти к требуемым по уравнениям (33), (43), (44). Во-вторых, можно получить полную выходную кривую сорбции и определить Δτ и τпр либо на одной и той же воде определить τпр для двух образцов с различными d экв.
|
|
|
Эффективный коэффициент диффузии можно вычислить на основании экспериментальных данных по формуле:
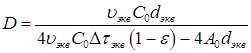 (45)
(45)
Порозность слоя адсорбента ε определяют, зная насыпную плотность сорбента ρн и кажущуюся плотность зерна сорбента ρк:
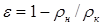 (46)
(46)
Если сорбент имеет несферическую форму, то эквивалентный диаметр d экв определяют по формуле
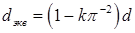 (47)
(47)
в которой d – диаметр частицы; k = 0,168; 0,45 и 0,6 при 2 l / d = 1; 4 и ∞, где l – длина цилиндрической частицы сорбента.
С другой стороны, L мп можно определить по формуле Майлкса – Трэйбола:
 (48)
(48)
где  – фактор симметричности выходных кривых, отражающий долю сорбата, поглощенного за время
– фактор симметричности выходных кривых, отражающий долю сорбата, поглощенного за время 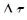 от всего количества пропущенного за это время сорбата; обычно 0,35 ≤ φ ≤ 0,55.
от всего количества пропущенного за это время сорбата; обычно 0,35 ≤ φ ≤ 0,55.
Работами Славинского показано, что при очистке воды в адсорберах с плотным слоем гранулированного сорбента продольная диффузия незначительна и режим движения жидкости в таком адсорбере с достаточной степенью точности можно описать моделью идеального вытеснения. Однако есть данные, что при сорбции фенола продольная диффузия вносит существенные изменения в динамику процесса. Это особенно важно для веществ с нелинейно изотермой сорбции и в начальный момент работы адсорбера. Также отмечено увеличение крутизны выходной кривой сорбции фенола с ростом высота слоя сорбента. Используя близость значений φ и ε, предложено в расчетах использовать формулу следующего вида:
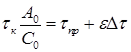 (49)
(49)
где 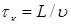 .
.
При изучении поглощения ряда ароматических соединений было найдено, что длина зоны массопереноса L мп мало зависит от типа сорбата, С0 и общей длины адсорбера L 0. В то же время подтверждено, что L мп увеличивается с ростом v и d экв, но на нее влияет тип сорбата, С0 и скорость фильтрования v ф. При v ф = 5 – 25 м/ч, L мп = 0,15 – 0,5 м скорость движения границы массопередачи постоянна – 0,02 – 0,2 м/ч.
|
|
|
Все приведенной выше относилось к динамике сорбции из водных растворов индивидуальных загрязняющих веществ или таких многокомпонентных смесей, сорбционные свойства которых могут аппроксимироваться одним (условным) веществом. Кроме того, условием применения рассмотренных математических моделей является выпуклая форма изотермы: лишь в этом случае можно рассчитать длину зоны массопереноса. К сожалению, далеко не во всех случаях сорбционной очистки воды указанные условия выполняются.
Различия в сорбционных свойствах реальных вод (особенно сточных) сложного состава проскок плохо сорбируемых загрязнений через адсорбер наступает практически сразу и медленно, но неуклонно увеличивается при любой высоте адсорбера. Поэтому при очистке воды «проскоковую» концентрацию часто характеризуют параметром Спр = ( 0,05 – 0,20 )С0.
Сорбционный процесс в статических и динамических условиях протекает по-разному. В статических условиях при перемешивании сорбента и раствора в замкнутом объеме хроматографический эффект и экранирующее влияние грубодисперсных примесей отсутствуют. Так, введение до 12,5 г/л глины и до 10 мг/л полиэлектролитов в раствор фенола (обычно сильно уменьшающих емкость ГАУ при фильтровании воды) не влияло на его сорбцию в статических условиях. Для снижения эффекта хроматографического разделения примесей внутри адсорбера рекомендуется проводить процесс в кипящем слое адсорбента. У активных углей разделительные свойства сильнее проявляются при увеличении размеров микропор в условиях частичного (10 – 80%) заполнения адсорбционного пространства.
Наиболее изучена сорбция самых простых (бинарных) смесей загрязнений в водных растворах; для этого разработаны специальные методики. Выходную кривую при сорбции бинарной смеси можно разбить на 4 участка: плохосорбируемое вещество частично задерживается сорбентом; оно целиком идет на «проскок»; частично вымывается то, что сорбировалось на первой стадии, Ск > С0; проскок его снижается до Ск = С0, начинается проскок хорошо сорбируемого компонента; оба соединения полностью транзитом проходят адсорбер; С0 = Ск. При сорбции двух соединений одно из них может односторонне влиять на извлечение другого. Так, n-нитрофенол влияет на сорбцию фенола, а фенол не оказывает аналогичного воздействия.
При сорбции бинарных смесей углеводородов влияние свойств менее сорбируемых компонентов проявляется, в основном, не во фронте вытеснения, а во втором фронте, где происходит поглощение одного, менее сорбируемого компонента. Степень отработки адсорбента и концентрирования менее сорбируемых компонентов увеличивается с уменьшением скорости движения сорбента в слое.
|
|
|
Пример конкурентной сорбции – очистка сточных вод коксохимических заводов. Вначале на АУ извлекаются фенол (С0 = 200 мг/л, τпр = 1,5 – 2 ч), масла и смолы. Затем смолы и масла, как более сорбируемые, вытесняют фенол из крупных микропор АУ, и через 3 – 4 ч работы адсорбера концентрация фенола в «очищенной» воде на 10 – 20% превышает исходную. При такой работе емкость угля по фенолу и время защитного действия адсорбера в 2 – 3 раза ниже, чем при сорбции чистого фенольного раствора. [2]
|
|
|


