 |
Системы: изолированные, закрытые и открытые. Состояние системы. Функция состояния. Процессы: изобарные, изотермические, изохорные и адиабатические.
|
|
|
|
Система – это тело или групп тел, находящихся во взаимодействии, реально или мысленно обособленных от окружающей среды и подвергнутых изучению, рассматривающийся как совокупность большого числа частиц.
Системы бывают:
Открытые-обмениваются с окружающей средой и веществом, и энергией. Например: живой организм
Закрытые - обмениваются с окружающей средой и веществом, но не энергией. Например: теплообменники
Изолированные - отсутствует обмен веществом и энергией. Например: в природе не существует(модель – термостат)
Различают 3 состояния системы:
Равновесное-постоянство свойств во времени, отсутствие потоков вещества и энергии в системе
Стационарное - постоянство свойств во времени за счет непрерывного обмена веществом и энергией между системой и окружающей средой
Переходное - изменение свойств системы во времени
Если значение параметров не зависит от пути процесса, по которому система перешла в это состояние, то эти параметры называются - Функции состояния: Внутренняя энергия (U), энтропия(H), энтальпия(S),свободная энергия Гиббса(G)
Процесс – переход системы из одного состояния в другое, сопровождающийся необратимым или обратимым изменением хотя бы одного параметра, характеризующего данную систему.
Делятся на: Обратимые и необратимые.
1.Изотермические- T=const, ∆T=0
2. Изохорические- p=const, ∆p=0
3. Изобарические-V=const, ∆V=0
4. Адиабатические- Q= const, ∆Q=0
2.Внутренняя энергия системы. Работа. Теплота. Примеры систем и процессов различного типа, встречающихся в фармацевтической химии.
Внутренняя энергия (U) системы – это сумма потенциальной энергии взаимодействия всех частиц системы между собой и кинетической энергии их движения.
Внутренняя энергия системы складывается из поступательного и вращательного движения молекул, энергии внутримолекулярного колебательного движения атомов и атомных групп, составляющих молекулы, энергии вращения электронов в атомах, энергии, заключающейся в ядрах атомов, энергии межмолекулярного взаимодействия и других видов энергии. U=∑Uj, кДж/моль
Работа (А или W) – энергетическая мера направленных форм движения частиц в процессе взаимодействия системы с окружающей средой. Работа А считается положительной, если совершается системой против внешних сил окружающей среды.
Теплота (Q) – энергетическая мера хаотических форм движения частиц в процессе взаимодействия системы с окружающей средой.
В термодинамике коли-во теплоты считается положительным, если теплота сообщается системе из окружа. среды.
Работа и теплота не являются функциями состояния, а являются функциями процесса, их величина зависит от пути процесса, по которому система перешла из одного состояния в другое.
|
|
|
3.Первое начало термодинамики, его математическое выражение. Энтальпия. Изохорный и изобарный тепловой эффект реакции и соотношение между ними.
Формулировки:
1.Энергия не исчезает и не возникает из ничего, а только превращается из одного вида в другой в строго эквивалентных количествах.
2. В изомерных системах изменение U в р-те любых процессов равно 0. ∆U=0
3. Подведенная к закрытой системе теплота Q расходуется на совершение системой А против внешних сил. Q=∆U
Энтальпия (Н) – термодинамическая функция, характеризую-щая энергетическое состояние системы при изобарно-изотермических условиях. Химические реакции и физико-химические процессы могут протекать с выделением или поглощением энергии.
Количество теплоты, которое выделяется или поглощается при проведении химической реакции в изобарно-изотермических условиях Qр равно изменению энтальпии системы и называется энтальпией реакции (∆Н р-ции).
|
|
|
4.Закон Гесса. Термохимическое уравнение. Расчет стандартной теплоты химических реакций по стандартным энтальпиям образования и сгорания веществ.
Закон Гесса: Значение теплового эффекта процесса, протекающего в изобарных (Н р-ции) или изохорных (U р-ции) условиях, зависит только от начального и конечного состояния данной системы и не зависит от пути процесса.
Из закона Гесса вытекают следующие следствия:
1-е следствие используют для расчета энтальпии реакции по стандартным энтальпиям образования веществ.
∆Ho р-ции =∑ n i Ho обр. (прод. р-ции)- ∆Ho n i обр. (исх. в-в)
Стандартная теплота образования -это тепловой эффект реакции образования 1 моль в-ва из простых, находящихся в устойчивых агрегатных состояний.
2-е следствие используют для расчета теплового эффекта ре - акции по стандартным теплотам сгорания веществ.
Стандартная теплота сгорания вещества (Энтальпия сгорания) – это теплота, выделяющаяся при сгорании 1 моль вещества в кислороде до высших оксидов при стандартных условиях.
∆H o р-ции = ∆ H o n i сгор. (исх. в-в) - ∆H o n i обр. (прод. р-ции)
Тепловой эффект равен разности суммы энтальпий сгорания исх. В-в и продуктов с учетом стехиометрических коэффициентов
3-е следствие Тепловой эффект разложения какого-либо соединения равен и противоположен по знаку тепловому эффекту его образования. ∆H o обр. =- ∆ H o разл
5.Зависимость теплового эффекта химической реакции от температуры, ур-е Кирхгофа в дифференциальной и интегральной форме.
Зависимость: Иногда ∆Н0 зависит от t. Наличие этой зависимости и соли ее хар - р. определяется разностью теплоемкостей продуктов и реагентов.
∆Ср=∑ njCpj(прод)-∑njCp(исх. в-ва)
Уравнение Кирхгофа связывает между собой тепловой эффект р-ии (энтальпию) и изменение теплоемкости для изобарного и изохорного процесса.
В диф. форме  ;
;  )V
)V
В инт. форме  ; ∆Up=∆Uo(298)+Tинтеграл298∆СVdT
; ∆Up=∆Uo(298)+Tинтеграл298∆СVdT

6.Второе начало т/д, его математическое выражение. Изменение энтропии в изолированных системах. Расчет изменения энтропии при изотермических процессах (фазовые переходы) и изменение t.
2 Закон т/д Формулировки:
1) Теплота не может самостоятельно переходить от менее нагретого к более нагретому телу.
2) Невозможно создание вечного двигателя второго рода
3) В изолированных системах самопроизвольно могут совершаться такие процессы, в к-х энтропия возрастает.
4) В любой изолированной системе полная энергия остаётся постоянной, а полная энтропия со временем повышается. U=0, ∆S>0
Математическая формулировка:  или ∂Qобр=TdS
или ∂Qобр=TdS
В изолированной системе: ∂Qобр=0, dS=0, ∆S=0
|
|
|
7.Третье начало т/д. Абсолютное значение энтропии. Стандартное значение энтропии.
В системе при постоянных t и р. самопроизвольно могут протекать те процессы, которые приводят к уменьшению энергии Гиббса.
Третье начало термодинамики (теорема Нернста) — физический принцип, определяющий поведение энтропии при приближении температуры к абсолютному нулю. Является одним из постулатов термодинамики, принимаемым на основе обобщения значительного количества экспериментальных данных.
Третье начало термодинамики может быть сформулировано так: «Приращение энтропии при абсолютном нуле температуры стремится к конечному пределу, не зависящему от того, в каком равновесном состоянии находится система». 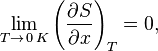
Итак, третий закон термодинамики (постулат Планка) позволяет вычислить так называемое абсолютное значение энтропии для веществ в любом агрегатном состоянии, если известны экспериментальные значения теплоемкостей от Т = 0 К до данной температуры, а также теплоты и температуры фазовых переходов. Уравнение для вычисления энтропии вещества в газообразном стандартном состоянии будет иметь вид: 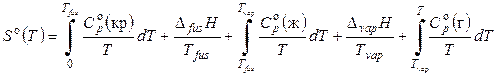
Аналогично могут быть вычислены значения стандартных энтропий веществ
 , то есть энтропий веществ при стандартных условиях (вещество находится в стандартном состоянии при температуре 298,15 К). Значения стандартных энтропий веществ приводятся в справочниках по термодинамическим свойствам веществ.
, то есть энтропий веществ при стандартных условиях (вещество находится в стандартном состоянии при температуре 298,15 К). Значения стандартных энтропий веществ приводятся в справочниках по термодинамическим свойствам веществ.
Из сопоставления значений стандартных энтропий веществ можно заключить, что:
– величина стандартной энтропии увеличивается при повышении массы частицы;
– стандартная энтропия ниже в ковалентно связанных твердых веществах с прочными, пространственно направленными связями (например, у алмаза меньше, чем у графита);
– при прочих равных условиях чем выше асимметрия молекулы, тем больше стандартная энтропия;
– стандартные энтропии газов (за исключением водорода) близки по величине и обычно значительно выше, чем энтропии жидкостей и твердых веществ, состоящих из молекул сравнимой сложности (газы менее упорядочены, чем жидкости или твердые вещества);
– стандартная энтропия газа уменьшается при его растворении в воде или в других растворителях;
– стандартная энтропия твердого вещества или жидкости возрастает при их растворении в воде или в других растворителях.
|
|
|
8.Т/д потенциалы. Энергия Геймгольца (изохорно-изотермический потенциал). Энергия Гиббса (изобарно-изотермический потенциал) Изменение энергии Геймгольца и энергии Гиббса в самопроизвольных процессах.
Свободной энергией Геймгольца – т/д ф-ию состояния, удовлетворяющую ур-ю: А-U-TS. Другое название свободной энергии-изохорно- изотермический потенциал.
В самопроизвольном процессе при постоянных t и V, когда совершается только работа расширения, свободная энергия Геймгольца уменьшается.
Свободная энергия Гиббса называется т/д ф-ию состояния, удовлетворяющую уравнению:
G=U+pV-TS
В самопроизвольном процессе при постоянных t и p, когда совершается только работа расширения, свободная энергия Гиббса уменьшается.
9. Уравнение изотермы хим. р-ии. Константа хим. Равновесия и способы ее выражения. Примеры использования констант равновесия хим. р-ии в фар. практике.
Уравнение изотермы: ∆G р-ии= RT(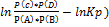 или ∆G р-ии= ∆G0р-ии +RT
или ∆G р-ии= ∆G0р-ии +RT 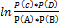
Кр-const хим. р-ии равновесия 
10. Уравнение изобары и изохоры хим. р-иии. Связь с принципом Ле-Шателье. Расчеты const хим. равновесия с помощью таблиц т/д величин.
Уравнение изобары: 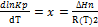 Уравнение изохоры:
Уравнение изохоры: 
11. Гомогенная и гетерогенная системы. Фазы. Составляющие в-ва. Компоненты. Число компонентов и число степеней свободы. Правило фаз Гиббса.
Гомогенные реакции – протекают при отсутствии поверхности раздела между реагентами по всему объему системы, т.е. в пределах одной фазы, например в смеси газов или веществ в растворе. Примером гомогенной реакции в газовой фазе может служить взаимодействие водорода и йода с образованием йодоводорода: H2(г) + I2 (г) = 2HI(г). Примером гомогенной реакции в растворе является: NaOH(р-р) + HCl(р-р) NaCl(р-р) + Н2О(ж)
Гетерогенные реакции – протекают на границе раздела фаз между реагентами, поэтому скорость гетерогенной реакции зависит от концентрации подвижного компонента (газа, растворенного вещества), от площади поверхности раздела фаз, от скорости диффузии подвижного компонента в зону реакции, а продуктов реакции – из этой зоны.
Фаза -часть гетерогенной системы, ограниченная поверхностью раздела и хар-ся одинаковыми физ., хим., и т/д св-ми во всех своих точках. (Бывают: Однофазные, двухфазные, трехфазные, многофазные)
Компонент(К)- индив хим. в-ва, составляющие часть системы, может быть выделена из них и существовать самостоятельно.
Число К- наличие числа индивидуальных хим. в-в, необходимые для образования всех фаз системы.
По числу К: Однокомпонентные, двухкомпонентные и т.д.
Число степеней свободы (ЧСС): число т/д параметров, определяющих состояние системы, к-е можно произвольно изменить без изменения числа фаз системы.
По ЧСС системы бывают: инвариантные (с=0), моновариантные (с=1), бивариантные (с=2) и т.д.
Правило фаз Гиббса: равновесие в системе может нарушиться при изменение внутренних параметров (t,p), при этом изм М компонентов, или исчезнет старые и появятся новые фазы, изменение происходит до установления равновесия С=К-Ф+n, где n- число параметров.
|
|
|
12.Диаграммы состояния однокомпонентных систем(вода).Уравнение Клапейрона, ур-е Клайперона-Клаузиуса. Связь с принципом Ле-Шателье. Прогнозирование фазовых переходов при изменении условий.
Простые однокомпонентные системы содержат только одно в-во, к-е может находиться в разных состояниях.
Диаграмма состояния воды:
Графическое изображение зависимости p от t или от состава. Диаграммы позволяют проводить анализ без выделения индивидуальных компонентов. Даже при небольшом изменении одного из параметров нарушается равновесии и приводит к исчезновению одной или двух фаз.
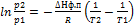 Или Уравнение Клайперона-Клаузиуса:
Или Уравнение Клайперона-Клаузиуса: 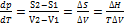

| p T | Ф=1 С=1-1+2=2 Имеются 3 поля: льда (Т), жидкости (Ж), пара (П) В пределах каждого поля можно менять t и p без Изменения числа фаз, т.к. при Ф=1. С=2. Кривые АО, ВО, СО хар-ют те значения p и t, при которых в системе имеются в равновесии 2 фазы. |
Система моновариантная -можно изменить только p и t. Второй параметр изменяется в зависимости от 1.
|
|
|


