 |
Методы временного запаздывания
|
|
|
|
а) Времена запаздывания. Понятие времени запаздывания, введенное Гарднером, широко используется в стандартной интерпретации данных МПВ главным образом благодаря тому, что многочисленные алгоритмы, основанные на использовании времен запаздывания, дают довольно точные результаты. Если принять, что времена вступления преломленной волны уже исправлены за рельеф и ЗМС, то время запаздывания, относящееся к траектории SMNG на рис. 2, представляет собой наблюдаемое время вступления преломленной волны в точку G (tg) минус время, затраченное волной на прохождение пути от точки Р до точки Q (проекция траектории на преломляющую границу) со скоростью V 2. Обозначив время запаздывания буквой d, запишем
 (1)
(1)
где d S и dg называют временами запаздывания впункте взрыва и в пункте приема соответственно, поскольку они связаны с участками траектории, идущими вниз от источника и вверх к приемнику.
Приближенное значение d найдем, приняв, что наклон границы достаточно мал и отрезок PQ приблизительно равен удалению сейсмоприемника х. В этом случае
 (2)
(2)
При наклоне границы менее 10° это соотношение дает удовлетворительную точность результатов для решения большинства задач. Если подставить значение tg, то становится ясно, что d равно t 0 только в случае горизонтальной границы.

Рис. 2. Иллюстрация к понятию времени запаздывания.
В литературе описано много способов интерпретации, использующих время запаздывания. Например, такие способы предложены Гарднером, Бартелмсом, Таррантом, Виробеком, Барри. Рассмотрим только три последних. Методы, описанные Виробеком и Таррантом, подходят для одиночных годографов, метод Барри дает наилучшие результаты в случае встречных годографов.
|
|
|
б) Метод Барри. Схема, описанная Барри, подобно многим, основанным на временах запаздывания, требует разложения полного времени запаздывания d на составляющие члены dS и dg. На рис. 3 изображен приемник R, который регистрирует колебания от источников A и В. Луч BN отражается под критическим углом; следовательно, Q — первый приемник, который зарегистрирует головную волну, порожденную источником В. Пусть d ам — время запаздывания в пункте взрыва A, d nq иd PR — времена запаздывания в пунктах приема Q и R, a d aq иd ar — полные времена запаздывания для траекторий AMNQ и AMPR..
Тогда

Время запаздывания в пункте взрыва В d BN, в случае если наклон границы мал, приблизительно равно времени запаздывания в пункте приема Q d NQ. Следовательно,

 .
.
Времена запаздывания в пунктах приема теперь можно записать в следующем виде:
 (3)
(3)
Таким образом, время запаздывания в пункте приема R можно получить, если имеются данные для двух пунктов взрыва

Рис. 3. Определение времен запаздывания в пункте взрыва и пункте приема.
с одной стороны от приемной расстановки и можно найти точку Q. Если принять, что вблизи N граница горизонтальна и находится на глубине hN, можно записать
 (4)
(4)
 (5)
(5)
Принимаем, что время запаздывания d bn равно половине t 0 в точке В; это позволяет рассчитать приближенное значение BQ и определить таким образом времена запаздывания для всех сейсмоприемников вправо от Q, которые зарегистрировали колебания, возбужденные в точках А и В.
Этот способ интерпретации включает следующие шаги, которые можно проследить по рис.4:
а) построение годографов по исправленным временам;
б) расчет и построение графиков полных времен запаздывания для всех положений приемников;
в) расчет «сейсмического сноса для сейсмоприемников» (РР' на рис. 4) с помощью соотношения РР' ≈ V 2 d PR tg 2 Q, после чего кривые времен запаздывания в п. (б) сдвигаются по направлению к пункту взрыва на эти величины;
|
|
|
г) смещенные на этапе (в) кривые для встречных профилей должны быть параллельны; любое расхождение обусловлено
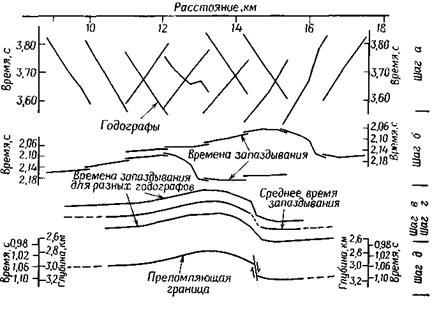
Рис. 4. Интерпретация встречных профилей по методу времен запаздывания.
неточным выбором значения V 2; следовательно, значение V 2 необходимо исправить и повторить этапы (б), (в), пока кривые не станут параллельны (на практике уточнение V 2 обычно производится только один раз);
д) разделение полных времен запаздывания на относящиеся к пунктам взрыва и пунктам приема (при этом последние относят к проекциям на поверхность точек, в которых сейсмическая волна падает на преломляющую границу и отходит от нее, т. е. к точкам S и Т на рис. 3); масштаб времен, если требуется, можно перевести в масштаб глубин с помощью формулы (4).
в) Метод Тарранта. В этом методе времена запаздывания используются для определения положения точки Q (рис. 5, а), в которой энергия, регистрируемая в пункте R, отходит от границы. Обозначив dg время запаздывания, связанное с траекторией QR, запишем
 ,
,
Откуда
 . (6)
. (6)
Мы получили уравнение эллипса в полярной системе координат. Эллипс —это геометрическое место таких точек Q (рис. 5, б),
|
|
Рис. 5. Интерпретация по методу Тарранта а — связь между точкой приема К и точкой Q отхода от границы; б —схема, поясняющая, что геометрическим местом точек Q является эллипс, в одном из фокусов которого располагается точка R; в — геометрия эллипса, проходящего через точку Q.
для которых отношение QR / QM остается постоянным (равным эксцентриситету e, который для эллипса меньше 1, т. е.
r/(h + rcosj) = e,
а следовательно,
r = e h /(1 - ecosj). (7)
Большая ось эллипса 2а = rj=0 + rj=p = 2 e h / (1—e2). Малую полуось b можно найти, записав y = rsinjи определив у max,; это дает b = e h ( 1— e2)-1/2. Расстояние от фокуса R до центра эллипса О равно
r|j=0 — а = e h /(1 — e) —e h /(1 — e2) = e a.
Если принять e = sinQ и h = V 2dg, выражение (7) перейдет в (6).
Для горизонтальной преломляющей границы получается эллипс (рис. 5, в) с а = V 2 d g tgQsecQ, b = V 2 d g tgQи OR = V 2 d g tg2Q. Подобным же образом RQ = b / cos Q = а и Ð OQR = arctg(О R / b) = Q, OQ = OR ctgQ = V 2 d g tgQ.
|
|
|
В окрестности Q эллипс можно аппроксимировать окружностью того же радиуса кривизны. Если записать уравнение эллипса в декартовой системе координат
(x / a)2+(y / b)2 = 1,
то радиус кривизны r можно выразить как
r = (1+ y ’ 2)3/2/ y ’’,
где у' = — (b /а)2(х + у) и у" = —(b /а)2(у — ху')/у2; в точке Q у' = 0 и у" = b /а2. Следовательно,
r = a 2 lb = V 2 d g /cos3Q = V 2 d g tgQsec2Q
и центр кривизны С лежит в точке (0, r — b), т. е. (0, V 2 d g tg3Q). Следовательно, Ð CRO = arctg (CO / RO) = Q, а значит, Ð CRQ — прямой угол.
Чтобы применить описанный метод, мы должны определить скорости V 1и V 2 и время запаздывания в пункте взрыва dS, а затем рассчитать dg по формуле
dg = tR — x / V 2 — dS.
После этого можно вычислить OR, OQ и затем найти положение С, проведя перпендикуляр RC к RQ. Из С проводим дугу окружности, соответствующую преломляющей границе в окрестности точки Q. Если наклон границы отличен от нуля, точкой выхода станет Q ' и длина дуги QQ ' увеличивается при росте угла наклона границы. Но даже для углов падения умеренной величины дуга эллипса QQ ' будет близка к дуге окружности, проходящей через Q, и, таким образом, огибающая дуг окружностей достаточно точно отобразит преломляющую границу.
Метод Тарранта удобен, когда наклон границ умеренный или даже большой, а преломляющая граница криволинейна или имеет неправильную форму. Принципиальным ограничением является точность определения V 2.
г) Метод Виробека. Для иллюстрации метода Виробека обратимся к верхней части рис. 6, где показан ряд одиночных годографов. Последовательные шаги интерпретации таковы:
а) строят исправленные годографы и измеряют времена t 0, отсекаемые годографами на оси t;
б) рассчитывают полное время запаздывания d для каждого положения приемников при каждом положении пункта взрыва и наносят полученные значения в точках приема (если нужно, принимают некоторое значение V 2); сдвигая отдельные участки вверх и вниз, получают сводную кривую запаздывания, отражающую конфигурацию мнимого горизонта;
в) строят график времени t 0, деленного на 2, и сопоставляют его со сводной кривой запаздывания; расхождение между двумя
|
|
|
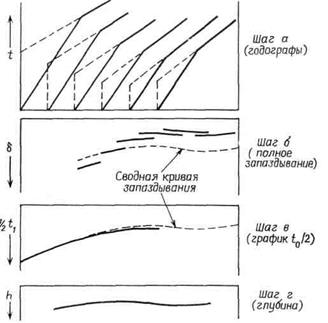
Рис. 6. Интерпретация профилей, отработанных в одном направлении, по методу Виробека.
кривыми указывает на то, что значение V 2 выбрано неверно (см. ниже), поэтому значение, использованное на шаге (б), следует уточнять, пока две кривые не станут «параллельны», после чего кривую t 0 /2 дополняют путем интерполяции и экстраполяции так, чтобы она покрывала тот же диапазон, что и сводная кривая временных задержек;
г) кривую t 0 /2 преобразуют в кривую глубин, используя выражение
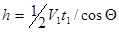
Успех применения метода Виробека зависит от того, является ли кривая d приблизительно параллельной кривой t 0 /2 Чтобы применять данный метод, не требуется встречных профилей, так как t 0 не зависит от направления, в котором развернута приемная коса.
Методы временного запаздывания подвержены некоторым ошибкам, которых следует избегать. По мере увеличения расстояния приемника от пункта взрыва цуг преломленных волн становится длиннее и максимум энергии сдвигается в сторону более поздних периодов. Поэтому возникает опасность, что на разных профилях прокоррелированными окажутся разные периоды и что ошибка будет интерпретироваться как увеличение временного запаздывания в пункте взрыва. Если имеется достаточно данных, ошибка будет, как правило, очевидна. Изменения в скорости преломленной волны проявляются в локальных расхождениях кривых полного временного запаздывания в зависимости от удаления для пар встречных годографов. Однако, если использованы годографы, не соответствующие на самом деле волне, преломленной на рассматриваемой границе, вид графиков оказывается таким же, как если бы менялась граничная скорость. В случаях когда имеется несколько преломляющих границ, которые характеризуются почти одинаковыми граничными скоростями, однозначная интерпретация может оказаться невозможной.
|
|
|



