 |
Кинетический момент твердого тела
|
|
|
|
Система Кенига. Теоремы Кенига
Пусть система отсчета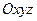 
неподвижная (инерциальная). Система 
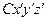движется поступательно по отношению к 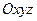, причем ее начало во все время движения совпадает с центром масс механической системы (Рис.4.3). Такая система координат называется системой Кенига. Следует заметить, что система Кенига играет исключительно важную роль при описании движения твердого тела.
Установим связь между кинетическими моментами механической системы относительно неподвижного центра 
и относительно центра масс механической системы 
. По определению кинетического момента (4.9):
(4.27)
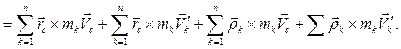
Здесь 
– скорость точки 
по отношению к системе Кенига.
Вычислим каждую из четырех сумм, входящих в равенство (4.27).
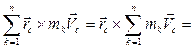
где 
– масса всей системы.
здесь использована формула (4.12) и учтено, что центр масс тела в подвижной системе координат покоится 
здесь использована формула (4.12) и учтено, что 
, поскольку центр масс тела всегда совпадает с началом подвижной системы координат. Последняя сумма представляет собой кинетический момент механической системы отноcительно центра масс в системе Кенига:
Подставляя полученные результаты в формулу (4.27), находим:
(4.28)
Равенство (4.28) составляет содержание первой теоремы Кенига.
При вычислении кинетической энергии часто бывает полезной, так называемая, вторая теорема Кенига, устанавливающая связь между кинетической энергией механической системы относительно неподвижной системы отсчета и кинетической энергией, полученной системой в относительном движении по отношению к системе координат Кёнига.
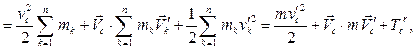
где 
– кинетическая энергия, полученная механической системой в ее относительном движении по отношению к системе Кенига. Поскольку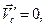 
окончательно получаем:
|
|
|
(4.29)
Теорема об изменении кинетического момента относительно центра масс механической системы
Подставим результат (4.28) в теорему об изменении кинетического момента относительно неподвижного центра (4.10):
или
Второе слагаемое в левой части равенства равно нулю, как векторное произведение коллинеарных сомножителей. Используя теорему о движении центра масс (4.15), получаем:
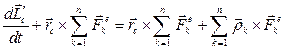
или
(4.30)
Таким образом,
производная по времени от кинетического момента механической системы относительно ее центра масс равна сумме моментов относительно центра масс всех приложенных к системе внешних сил.
Как видно, теорема об изменении кинетического момента сохраняет свой вид, если в качестве моментной точки используется центр масс механической системы.
Движение абсолютно твердого тела
Кинетический момент твердого тела
В разделе "Кинематика твердого тела" установлено, что свободное абсолютно твердое тело имеет шесть степеней свободы, т.е. его положение в системе отсчета в любой момент времени определяется шестью параметрами – координатами. В качестве таких координат удобно использовать три декартовы координаты произвольно выбранной точки, принятой за полюс, и три угла (например, углы Эйлера), определяющие положение тела по отношению к подвижной системе координат, движущейся поступательно со скоростью точки, принятой за полюс.
В динамике за полюс принимают центр масс тела. Это связано с тем, что наличие теоремы о движении центра масс механической системы (4.15) позволяет определить закон движения такого полюса – точки . Остается определить движение тела по отношению к осям Кенига, что можно сделать, используя теорему об изменении кинетического момента относительно центра масс механической системы (4.30).
|
|
|
В общем случае движения свободного твердого тела получаем, записывая векторные уравнения (4.15) и (4.30) в проекциях на соответствующие оси координат, шесть скалярных уравнений, которые позволяют определить закон движения тела. В частных случаях движения число уравнений, естественно, уменьшается.
Введенный ранее кинетический момент, определен как сумма моментов количеств движения для всех материальных точек, образующих механическую систему. Абсолютно твердое тело определяется как геометрически неизменяемая механическая система, масса которой непрерывным образом распределена по объему, занятому системой. При вычислении кинетического момента тело мысленно разбивается на частицы и определяется предел последовательности кинетических моментов для системы частиц при массе частицы стремящейся к нулю (число частиц при этом стремится к бесконечности):
При вычислении подобных интегралов необходимо перейти к интегрированию по объему, полагая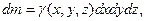 
где 
– плотность тела.
В общем случае свободного твердого тела его движение по отношению к осям Кенига будет сферическим. Вычислим кинетический момент тела, совершающего сферическое движение, относительно шарнирно закрепленной точки.
– вектор мгновенной угловой скорости тела;
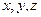– текущие координаты точки;
– орты осей, жестко связанных с телом.
Записывая полученное равенство в проекциях на координатные оси, находим:
(5.1)
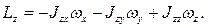
Величины
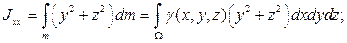
(5.2)
называются моментами инерции тела относительно координатных осей (
– объем тела).
Величины
(5.3)
называются центробежными моментами инерции или произведениями инерции.
Моменты инерции
Моменты инерции характеризуют распределение массы в теле и играют существенную роль в описании движения твердого тела. При вычислении моментов инерции обычно используют координатные оси жестко связанные с телом. Причина простая – в таких осях моменты инерции постоянны (не зависят от времени).
Осевые моменты инерции всегда положительны. В нуль осевой момент инерции может обратиться только в одном частном случае, когда можно считать, что вся масса тела распределена по оси, относительно которой вычисляется момент инерции (например, относительно продольной оси балки). В отличие от осевых, центробежные моменты инерции могут иметь любой знак и обращаться в нуль.
|
|
|
Вместо осевого момента инерции иногда используют радиус инерции тела относительно оси, под которым понимают расстояние от оси до точки, в которой нужно сосредоточить массу всего тела, чтобы момент инерции точки относительно данной оси равнялся моменту инерции тела относительно той же оси:
|
|
|
