 |
Вычисление кинетической энергии абсолютно твердого тела
|
|
|
|
Получим формулы для вычисления кинетической энергии абсолютно твердого тела при некоторых его движениях.
1. При поступательном движении в любой момент времени скорости всех точек тела одинаковые. Полагая в формуле (4.18)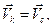 
получаем:
(5.6)
где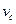 
– скорость центра масс тела.
2. При вращении скорости точек тела пропорциональны расстояниям от точек до оси вращения. Полагая в формуле (4.18)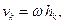 
получаем:
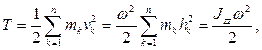(5.7)
где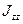 
– момент инерции тела относительно оси вращения.
3. При плоско–параллельном движении тело по отношению к системе Кенига совершает вращение вокруг оси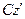 
. Используя вторую теорему Кенига (4.32) и формулу (5.7), получаем:
(5.8)
где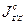 
– момент инерции тела относительно оси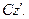 
Работа внутренних сил геометрически неизменяемой механической системы
Заметим, что в отличие от теоремы об изменении количества движения и теоремы об изменении кинетического момента в теорему об изменении кинетической энергии в общем случае входят внутренние силы.
Особый случай представляет геометрически неизменяемая механическая система, в частности, абсолютно твердое тело.
Скорости двух любых точек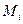 
и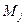 
геометрически неизменяемой механической системы связаны известным кинематическим соотношением:
причём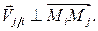 
Эти две точки взаимодействуют с силами равными по модулю и направленными по одной прямой в противоположные стороны:
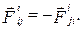
Заметим, что для механической системы эти силы являются внутренними.
Вычислим суммарную мощность этих двух сил:
т.к. 
Поскольку внутренние силы действуют попарно, получаем, что суммарная мощность, а следовательно, и суммарная работа всех внутренних сил геометрически неизменяемой механической системы равна нулю при любых ее перемещениях.
|
|
|
Для геометрически неизменяемой механической системы теорема об изменении кинетической энергии является прямым следствием теоремы об изменении количества движения и теоремы об изменении кинетического момента. Тем не менее, ее использование часто оказывается удобным, особенно в тех случаях, когда необходимо определить зависимость каких–либо скоростей от перемещения, совершенного системой. Для геометрически изменяемой механической системы теорема об изменении кинетической энергии носит независимый характер.
Работа внешних сил, приложенных к абсолютно твердому телу
В разделе "Кинематика" установлено, что скорость любой точки твердого тела геометрически складывается из скорости точки, принятой за полюс, и скорости, полученной точкой при сферическом движении тела вокруг полюса. В динамике за полюс всегда принимают центр масс тела. Скорость любой точки тела определяется по формуле
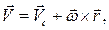
где
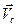– скорость центра масс тела;
– вектор мгновенной угловой скорости тела;
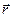– радиус-вектор по отношению к центру масс тела.
Для мощности силы, приложенной к абсолютно твердому телу, получаем:
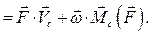
Особый интерес представляет плоско–параллельное движение твердого тела. В этом важном частном случае мощность силы может быть вычислена по формуле:
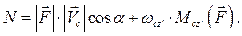
где 
– угол между векторами силы и скорости центра масс тела.
Некоторые частные случаи вычисления работы силы
Работа силы тяжести
При вычислении работы силы тяжести будем считать, что мы рассматриваем ограниченную область пространства вблизи поверхности Земли, размеры которой малы по сравнению с размерами Земли.
Направим ось 
вертикально вверх. Точка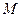 
с массой 
перемещается по некоторой траектории из положения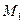 
в положение 
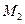(Рис.5.7). Проекции силы тяжести на оси координат равны: 
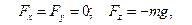где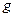 
– ускорение свободного падения.
|
|
|
Вычислим работу силы тяжести. Используя формулу (4.21), получаем:
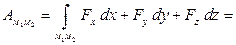
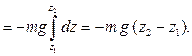
Как видно, сила тяжести – потенциальная сила. Ее работа не зависит от траектории точки, а определяется перепадом высот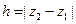 
между начальным и конечным положениями точки.
Таким образом,
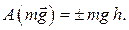(5.9)
Работа силы тяжести положительна, если точка теряет высоту (опускается) и отрицательна, если точка набирает высоту.
Работа упругой силы
Понятие упругой силы обычно ассоциируется с реакцией линейно–упругой пружины. Направим ось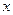 
вдоль пружины в сторону ее растяжения. Под 
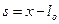понимаем удлинение пружины (
– длина нерастянутой пружины).
Сила реакции пружины пропорциональна ее удлинению 
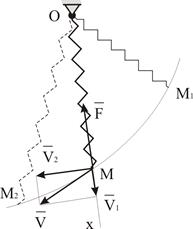
где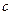 
– коэффициент жесткости пружины. Разложим вектор скорости точки 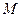на две составляющие, одна из которых 
направлена вдоль пружины и определяет скорость ее растяжения, а вторая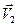 
перпендикулярна пружине и определяет скорость точки 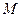, полученную при повороте пружины без изменения ее длины (Рис.5.8).
Вычислим мощность упругой силы:
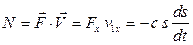так как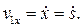 
Работа упругой силы при перемещении конца пружины из 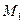в 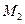оказывается равной
Как видно, упругая сила потенциальна. Заметим, что если поворачивать пружину вокруг шарнира 
, не изменяя ее длины, то упругая сила не совершает работу.
| 
| |
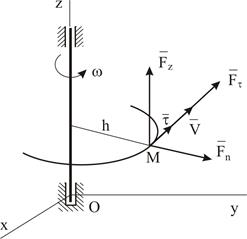
| Рис. 5.8 | Рис. 5.9 |
Работа вращающего момента
Пусть сила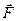 
приложена в некоторой точке тела, имеющего ось вращения. Тело вращается с угловой скоростью 
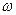. Вычислим мощность и работу силы. Точка приложения силы описывает окружность. Разложим силу на составляющие по осям естественного трехгранника (Рис.5.9):
Работу будет совершать только составляющая 
, направленная по касательной к траектории точки :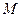
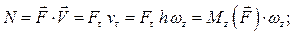
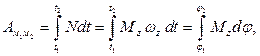(5.10)
где 
– момент силы 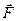относительно оси вращения тела.
|
|
|
