Дендрограмма (кластерный анализ)

Если сравнивать несколько участков, хорошее представление о бета-разнообразии может дать кластерный анализ.

Кластерный анализ – один из методов многомерного анализа, сущность которого состоит в иерархической классификации объек­тов в разделении множества объектов на однородные группы. Гра­фически иерархическая классификация отображается в виде дендрограммы (дерева).

Внутри каждой группы, получаемой в результате разбиения объектов на кластеры (группы), объекты более сходны, чем с объек­тами из других групп. Кластерный анализ начинается с составле­ния матрицы сходства для каждой пары сравниваемых объектов. Затем проводится последовательное объединение объектов в груп­пы по степени их сходства, пока все они не будут включены в одну группу. Поскольку интерпретация результатов кластерного анали­за зависит от визуальной оценки дендрограммы, лучше всего ис­пользовать этот прием для малых массивов данных.

В качестве примера рассмотрим кластеризацию выборок на ос­нове матрицы индексов сходства (табл. 5.8.1). Простейшие методы кластерного анализа, применяемого в биоценологии, биогеографии и числовой таксономии разными авторами, описаны Ю. А. Песенко [1982]. Эти методы могут быть с успехом использованы и в эколо­гических исследованиях при анализе бета-разнообразия.

Рис. 5.8.4. Дендрограмма кластерного анализа шести объектов, построенная методом одиночного присоединения (ближайшего соседа)

В наиболее простых случаях процесс группировки начинается с нахождения в матрице индексов сходства пары наиболее сходных объектов. Самыми близкими объектами в примере, рассмотренном в табл. 5.8.1, являются Г и Д (0,90). Эти объекты отображаются на гра­фике двумя соседними точками (рис. 5.8.4).

Отходящие от точек параллельные линии соединяются отрез­ком на уровне величины сходства и объединяются в один кластер. Затем в матрице индексов сходства находится второй по величине индекс сходства. Если он связывает два других, еще не объединен­ных в группу объекта, то их соединяют так же, как и первые два, но отдельно от них на соответствующем уровне сходства. В нашем примере вторая по силе связь имеется между объектами Г и В (0,85), при этом один из этих объектов уже объединен в кластер. В этом случае присоединение связанного с ним нового объекта может быть произведено тремя разными способами: одиночным, полным и сред­ним присоединением.

Одиночное присоединение называют также «методом ближнего соседа». Метод впервые использован Серенсеном в 1948 году. Соеди­нение групп производится по максимальному значению сходства между объектами из каждой группы. Следуя этому методу, объект В присоединяется к объектам ДГ, уже объединенным в кластер. Следующее по величине сходство – между объектами А и Б (0,80). Они объединяются в отдельный кластер на уровне сходства. Следующий шаг – присоединение объекта Е к группе из объединен­ных ранее объектов ДГВ, так как между объектами Е и Г сходство равно 0,75. На последнем этапе объединяются два сформирован­ных ранее кластера ДГВЕ и АБ в один на уровне 0,60. Результаты объединения показаны на рис. 5.8.4.

Полное присоединение называется также «методом дальнего соседа». Метод был впервые предложен Снитом в 1957 году Соглас­но этому правилу, после формирования кластеров ДГ и АБ к груп­пе АБ присоединяется объект Е, так как минимальное сходство этого объекта с объектами этого кластера равно 0,60. Объект В присоединяется к группе ДГ только на уровне 0,15 (минимальное сходство с каждым из объектов группы). Этот объект нельзя при­соединить к кластеру ЕАБ, так как минимальное сходство объек­та Е с объектами этой группы всего 0,1. Результаты объединения показаны на рис. 5.8.5.

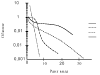
Рис. 5.8.5. Дендрограмма кластерного анализа шести объектов, построенная методом полного присоединения (дальнего соседа)

Среднее присоединение. Этот метод включает несколько вари­антов. Он был предложен в 1958 году Сокалом, Майченером и Олсоном, Миллером одновременно. Один из самых простых вариан­тов этого вида кластерного анализа заключается в использовании средних арифметических невзвешенных значений сходства при­соединенного объекта со всеми объектами группы. Соединяются кластеры, среднее сходство между объектами которых выше. Со­гласно этому методу, после формирования кластеров ДГ и АБ к группе АБ присоединяется объект Е, так как среднее сходство этого объекта с объектами этого кластера (0,6 + 0,65)/2 = 0,625. Этот объект нельзя присоединить к кластеру В (сходство всего 0,10) или кластеру ДГ (среднее сходство равно 0,50). На следующем шаге к группе ДГ присоединяется объект В, так как среднее сход­ство его с объектами данного кластера равно 0,5, а с группой ЕАБ – лишь 0,20. Последний шаг – объединение двух групп ДГВ и ЕАБ в один кластер на уровне 0,49, так как эта величина пока­зывает среднюю связь между объектами в двух группах. Резуль­таты объединения показаны на рис. 5.8.6.

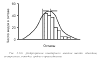
Рис. 5.8.6. Дендрограмма кластерного анализа шести объектов, построенная методом среднего присоединения

Более сложные и разнообразные методы кластерного анализа реализуются с помощью вычислительной техники. Разработано множество статистических пакетов программ, таких как Statgraphics, Statistica, STADIA и другие, которые выполняют кластерный анализ.