 |
Генеральная и выборочная совокупности
|
|
|
|
Основы математической статистики
Основные задачи и понятия математической статистики
Предмет математической статистики
Математическая статистика - раздел математики, в котором изучаются методы сбора, систематизации и обработки результатов наблюдений массовых случайных явлений для выявления существующих закономерностей.
Математическая статистика тесно связана с теорией вероятностей. Обе эти математические дисциплины изучают массовые случайные явления. Связующим звеном между ними являются предельные теоремы теории вероятностей. При этом теория вероятностей выводит из математической модели свойства реального процесса, а математическая статистика устанавливает свойства математической модели, исходя из данных наблюдений, т.е. из статистических данных.
Предметом математической статистики является изучение случайных величин (или случайных событий, процессов) по результатам наблюдений. Первая задача состоит в том, чтобы каким-либо образом обработать, т.е. упорядочить, представить в удобном для обозрения и анализа виде, полученные в результате наблюдения (опыта, эксперимента) данные. Вторая задача - оценить, хотя бы приблизительно, интересующие нас характеристики наблюдаемой случайной величины. Например, дать оценку неизвестной вероятности события, оценку неизвестной функции распределения, оценку математического ожидания, оценку дисперсии случайной величины, оценку параметров распределения, вид которого неизвестен, и т. д.
Третьей, задачей является проверка статистических гипотез, т. е. решение вопроса согласования результатов оценивания с опытными данными. Например, выдвигается гипотеза, что: а) наблюдаемая с. в. подчиняется нормальному закону; б) м. о. наблюдаемой с. в. равно нулю; в) случайное событие обладает данной вероятностью и т. д.
|
|
|
Одной из важнейших задач математической статистики является разработка методов, позволяющих по результатам обследования выборки (т.е. части исследуемой совокупности объектов) делать обоснованные выводы о распределении признака (случайной величины X) изучаемых объектов по всей совокупности.
Результаты исследования статистических данных методами математической статистики используются для принятия решения в задачах планирования, управления, прогнозирования и организации производства, при контроле качества продукции, при выборе оптимального времени настройки или замены действующей аппаратуры и т.д., т.е. для научных и практических выводов.
Говорят, что «математическая статистика - это теория принятия решений в условиях неопределенности».
Математическая статистика возникла в XVIII веке в работах Я. Бернулли, П. Лапласа, К. Пирсона. В ее современном развитии определяющую роль сыграли труды Г. Крамера, Р. Фишера, Ю. Неймана и др. Большой вклад в математическую статистику внесли русские ученые П.Л. Чебышев, А.М. Ляпунов, А.Н. Колмогоров, Б.В. Гнеденко и другие.
Генеральная и выборочная совокупности
Пусть требуется изучить данную совокупность объектов относительно некоторого признака. Например, рассматривая работу диспетчера (продавца, парикмахера,...), можно исследовать: его загруженность, тип клиентов, скорость обслуживания, моменты поступления заявок и т.д. Каждый такой признак (и их комбинации) образует случайную величину, над которой производят наблюдения.
Совокупность всех подлежащих изучению объектов или возможных результатов всех мыслимых наблюдений, производимых в неизменных условиях над одним объектом, называется генеральной совокупностью.
|
|
|
Более строго: генеральная совокупность - это случайная величина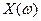 
, заданная на пространстве элементарных событий Ω с выделенным в нем классом S подмножеств событий, для которых указаны их вероятности.
Зачастую проводить сплошное обследование, когда изучаются все объекты (например - перепись населения), трудно или дорого, экономически нецелесообразно, а иногда невозможно. В этих случаях наилучшим способом обследования является выборочное наблюдение: выбирают из генеральной совокупности часть ее объектов («выборку») и подвергают их изучению.
Выборочной совокупностью (выборкой) называется совокупность объектов, отобранных случайным образом из генеральной совокупности.
Более строго: выборка - это последовательность 
независимых одинаково распределенных случайных величин, распределение каждой из которых совпадает с распределением генеральной случайной величины.
Число объектов (наблюдений) в совокупности называется ее объемом.
Конкретные значения выборки, полученные в результате наблюдений (испытаний), называют реализацией выборки и обозначают строчными буквами 
.
Метод статистического исследования, состоящий в том, что на основе изучения выборочной совокупности делается заключение о всей генеральной совокупности, называется выборочным.
Для получения хороших оценок характеристик генеральной совокупности необходимо, чтобы выборка была репрезентативной (или представительной), т.е. достаточно полно представлять изучаемые признаки генеральной совокупности. Условием обеспечения репрезентативности выборки является, согласно закону больших чисел, соблюдение случайности отбора, т.е. все объекты генеральной совокупности должны иметь равные вероятности попасть в выборку.
Различают выборки с возвращением (повторные) и без возвращения (бесповторные). В первом случае отобранный объект возвращается в генеральную совокупность перед извлечением следующего; во втором - не возвращается. На практике чаще используется бесповторная выборка.
Заметим, если объем выборки значительно меньше объема генеральной совокупности, различие между повторной и бесповторной выборками очень мало, его можно не учитывать.
В зависимости от конкретных условий для обеспечения репрезентативности применяют различные способы отбора:
|
|
|
- простой, при котором из генеральной совокупности извлекают по одному объекту;
- типический, при котором генеральную совокупность делят на «типические» части и отбор осуществляется из каждой части (например, мнение о референдуме спросить у случайно отобранных людей, разделенных по признаку пола, возраста,...);
- механический, при котором отбор производится через определенный интервал (например, мнение спросить у каждого шестидесятого...);
- серийный, при котором объекты из генеральной совокупности отбираются «сериями», которые должны исследоваться при помощи сплошного обследования.
На практике пользуются сочетанием вышеупомянутых способов отбора.
|
|
|
