 |
Статистическое распределение выборки. Эмпирическая функция распределения
|
|
|
|
Пусть изучается некоторая случайная величина X. С этой целью над случайной величиной X производится ряд независимых опытов (наблюдений). В каждом из этих опытов величина X принимает то или иное значение.
Пусть она приняла n 1 раз значение х 1, n 2 раз - значение x 2,..., nk раз - значение xk При этом  - объем выборки. Значения
- объем выборки. Значения  называются вариантами случайной величины X.
называются вариантами случайной величины X.
Вся совокупность значений случайной величины X представляет собой первичный статистический материал, который подлежит дальнейшей обработке, прежде всего - упорядочению.
Операция расположения значений случайной величины (признака) по неубыванию называется ранжированием статистических данных. Полученная таким образом последовательность  значений случайной величины X (где
значений случайной величины X (где  и
и  ) называется вариационным рядом.
) называется вариационным рядом.
Числа  , показывающие, сколько раз встречаются варианты
, показывающие, сколько раз встречаются варианты  в ряде наблюдений, называются частотами, а отношение их к объему выборки - частостями или относительными частотами
в ряде наблюдений, называются частотами, а отношение их к объему выборки - частостями или относительными частотами  , т.е.
, т.е.
 , ,
| (8.1) |
где  .
.
Перечень вариантов и соответствующих им частот или частостей называется статистическим распределением выборки или статистическим рядом.
Записывается статистическое распределение в виде таблицы. Первая строка содержит варианты, а вторая - их частоты  (или частости
(или частости  ).
).
Статистическое распределение выборки является оценкой неизвестного распределения. В соответствии с теоремой Бернулли относительные частоты  сходятся при
сходятся при  к соответствующим вероятностям
к соответствующим вероятностям  , т.е.
, т.е. 
 . Поэтому при больших значениях n статистическое распределение мало отличается от истинного распределения.
. Поэтому при больших значениях n статистическое распределение мало отличается от истинного распределения.
В случае, когда число значений признака (случайной величины X) велико или признак является непрерывным (т.е. когда случайная величина X может принять любое значение в некотором интервале), составляют интервальный статистический ряд.
|
|
|
В первую строку таблицы статистического распределения вписывают частичные промежутки  , которые берут обычно одинаковыми по длине:
, которые берут обычно одинаковыми по длине: 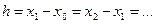 . Для определения величины интервала (h) можно использовать формулу Стерджеса:
. Для определения величины интервала (h) можно использовать формулу Стерджеса:
 ,
,
где  - разность между наибольшим и наименьшим значениями признака,
- разность между наибольшим и наименьшим значениями признака,  - число интервалов
- число интервалов  . За начало первого интервала рекомендуется брать величину
. За начало первого интервала рекомендуется брать величину  .
.
Во второй строчке статистического ряда вписывают количество наблюдений  , (
, (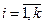 ), попавших в каждый интервал.
), попавших в каждый интервал.
Одним из способов обработки вариационного ряда является построение эмпирической функции распределения.
Эмпирической (статистической) функцией распределения называется функция  , определяющая для каждого значения х частость события
, определяющая для каждого значения х частость события  :
:
 . .
| (8.2) |
Для нахождения значений эмпирической функции удобно  записать в виде
записать в виде
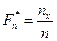
где n - объем выборки,  - число наблюдений, меньших x (x ÎR).
- число наблюдений, меньших x (x ÎR).
Очевидно, что  удовлетворяет тем же условиям, что и истинная функция распределения
удовлетворяет тем же условиям, что и истинная функция распределения  .
.
При увеличении числа n наблюдений (опытов) относительная частота события  приближается к вероятности этого события (теорема Бернулли). Эмпирическая функция распределения
приближается к вероятности этого события (теорема Бернулли). Эмпирическая функция распределения  является оценкой вероятности события
является оценкой вероятности события  , т.е. оценкой теоретической функции распределения
, т.е. оценкой теоретической функции распределения  случайной величины X.
случайной величины X.
Теорема 8.1 (Гливенко). Пусть  - теоретическая функция распределения случайной величины X, a
- теоретическая функция распределения случайной величины X, a  - эмпирическая. Тогда для любого
- эмпирическая. Тогда для любого 
 . .
| (8.3) |
Пример 8.1. В результате тестирования группа абитуриентов набрала баллы: 5, 3, 0, 1, 4, 2, 5, 4, 1, 5. Записать полученную выборку в виде: а) вариационного ряда; б) статистического ряда.
Решение:
а) Проранжировав статистические данные (т.е. исходный ряд), получим вариационный ряд  :
:
(0, 1, 1, 2, 3, 4, 4, 5, 5, 5).
б) Подсчитав частоту и частость вариантов  ,
,  ,
,  ,
,  ,
,  ,
,  , получим статистическое распределение выборки (так называемый дискретный статистический ряд)
, получим статистическое распределение выборки (так называемый дискретный статистический ряд)
|
|
|

| ||||||

|

или

| ||||||

| 
| 
| 
| 
| 
| 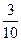
|

Пример 8.2. Построить функцию  используя условия и результаты задачи 8.1.
используя условия и результаты задачи 8.1.
Решение:
Здесь  . Имеем
. Имеем  при
при  (наблюдений меньше 0 нет). При
(наблюдений меньше 0 нет). При  при
при  (здесь
(здесь  ) и т.д. Окончательно получаем:
) и т.д. Окончательно получаем:

График эмпирической функции распределения приведен на рис. 8.1.

Рис.8.1.
|
|
|


