 |
Функция распределения двумерной случайной величины и ее свойства
|
|
|
|
Системы случайных величин
Двумерные случайные величины
Понятие о системе случайных величин и законе ее распределения
При изучении случайных явлений часто приходится иметь дело с двумя, тремя и большим числом случайных величин. Совместное рассмотрение нескольких случайных величин приводит к системам случайных величин. Так, точка попадания снаряда характеризуется системой  двух случайных величин: абсциссой X и ординатой Y; успеваемость наудачу взятого абитуриента характеризуется системой n случайных величин
двух случайных величин: абсциссой X и ординатой Y; успеваемость наудачу взятого абитуриента характеризуется системой n случайных величин 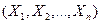 - оценками, проставленными в его аттестате зрелости.
- оценками, проставленными в его аттестате зрелости.
Упорядоченный набор 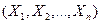 случайных величин
случайных величин 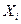
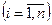 , заданных на одном и том же ПЭС Ω, называется n-мерной случайной величиной или системой n случайных величин.
, заданных на одном и том же ПЭС Ω, называется n-мерной случайной величиной или системой n случайных величин.
Одномерные случайные величины 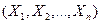 называются компонентами или составляющими n- мерной случайной величины
называются компонентами или составляющими n- мерной случайной величины 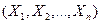 . Их удобно рассматривать как координаты случайной точки или случайного вектора
. Их удобно рассматривать как координаты случайной точки или случайного вектора 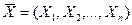 в пространстве n измерений.
в пространстве n измерений.
На многомерные случайные величины распространяются почти без изменений основные понятия и определения, относящиеся к одномерным случайным величинам. Ограничимся для простоты рассмотрением системы двух случайных величин; основные понятия обобщаются на случай большего числа компонент.
Упорядоченная пара  двух случайных величин Х и Y называется двумерной случайной величиной или системой двух одномерных случайных величин X и Y.
двух случайных величин Х и Y называется двумерной случайной величиной или системой двух одномерных случайных величин X и Y.
Систему  можно изобразить случайной точкой
можно изобразить случайной точкой 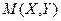 или случайным вектором ОМ (рис.6.1).
или случайным вектором ОМ (рис.6.1).
Система  есть функция элементарного события:
есть функция элементарного события: 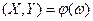 . Каждому элементарному событию
. Каждому элементарному событию 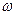 ставится в соответствие два действительных числа х и у (или х 1 и x 2) - значения X и Y (или
ставится в соответствие два действительных числа х и у (или х 1 и x 2) - значения X и Y (или 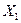 и
и 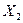 ) в данном опыте. В этом случае вектор
) в данном опыте. В этом случае вектор 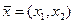 называется реализацией случайного вектора
называется реализацией случайного вектора  .
.
|
|
|
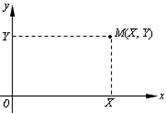
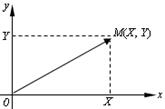
Рис. 6.1.
Системы случайных величин могут быть дискретными, непрерывными и смешанными в зависимости от типа случайных величин, образующих систему. В первом случае компоненты этих случайных систем дискретны, во втором - непрерывны, в третьем - разных типов.
Полной характеристикой системы  является ее закон распределения вероятностей, указывающий область возможных значений системы случайных величин и вероятности этих значений. Как и для отдельных случайных величин закон распределения системы может иметь разные формы (таблица, функция распределения, плотность,...).
является ее закон распределения вероятностей, указывающий область возможных значений системы случайных величин и вероятности этих значений. Как и для отдельных случайных величин закон распределения системы может иметь разные формы (таблица, функция распределения, плотность,...).
Так, закон распределения дискретной двумерной случайной величины  можно задать формулой
можно задать формулой
 , , 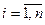 , , 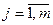
| (6.1) |
или в форме таблицы с двойным входом:

| 
| 
| 
| … | 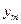
|
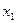
| 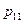
| 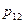
| 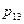
| … | 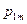
|
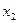
| 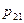
| 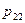
| 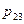
| … | 
|
| … | … | … | … | … | … |
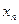
| 
| 
| 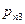
| … | 
|
Причем, сумма всех вероятностей  , как сумма вероятностей полной группы несовместных событий
, как сумма вероятностей полной группы несовместных событий  , равна единице:
, равна единице:
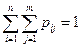 .
.
Зная закон распределения дискретной случайной величины, можно найти законы распределения каждой из компонент (обратное неверно). Так, 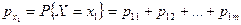 , что следует из теоремы сложения несовместных событий
, что следует из теоремы сложения несовместных событий 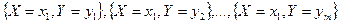 .
.
Аналогично можно найти
 ,
,
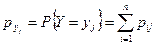 .
.
Пример 6.1. В урне 4 шара: 2 белых, 1 черный, 1 синий. Из нее наудачу извлекают два шара. Пусть случайная величина Х – число черных шаров в выборке, случайная величина Y – число синих шаров в выборке. Составить закон распределения для системы  . Найти законы распределения X и Y.
. Найти законы распределения X и Y.
Решение:
Случайная величина Х может принимать значения 0, 1; случайная величина Y - значения 0, 1.
Вычислим вероятности
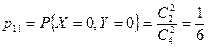 или
или  ,
,
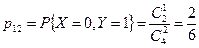 ,
,
 ,
,
 .
.
Таблица распределения системы  имеет вид:
имеет вид:

| ||
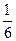
| 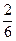
| |
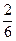
| 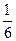
|
Отсюда следует:
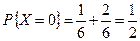 ,
,
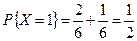 ,
,
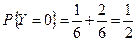 ,
,
 .
.
Законы распределения составляющих X и Y имеют вид:
| Х | Y | |||||||
| р | 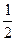
| 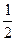
| р | 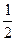
| 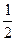
|
Функция распределения двумерной случайной величины и ее свойства
|
|
|
Универсальной формой задания распределения двумерной случайной величины является функция распределения (или «интегральная функция»), пригодная как для дискретной, так и для непрерывной случайной величины, обозначаемая 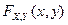 или просто
или просто 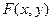 .
.
Функцией распределения двумерной случайной величины  называется функция
называется функция 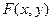 , которая для любых действительных чисел х и у равна вероятности совместного выполнения двух событий
, которая для любых действительных чисел х и у равна вероятности совместного выполнения двух событий  и
и 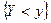 .
.
Таким образом, по определению

| (6.2) |
событие 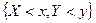 означает произведение событий
означает произведение событий  и
и 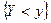 .
.
Геометрически функция 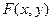 интерпретируется как вероятность попадания случайной точки
интерпретируется как вероятность попадания случайной точки  в бесконечный квадрант с вершиной в точке
в бесконечный квадрант с вершиной в точке 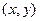 , лежащий левее и ниже ее (рис. 6.2).
, лежащий левее и ниже ее (рис. 6.2).

Рис. 6.2.
Функция распределения двумерной дискретной случайной величины  находится суммированием всех вероятностей
находится суммированием всех вероятностей  , для которых
, для которых 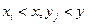 , т.е.
, т.е.
 . .
| (6.3) |
Геометрическая интерпретация функции распределения позволяет наглядно иллюстрировать ее свойства.
Свойства функции распределения двумерной случайной величины:
1. Функция распределения 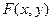 ограничена, т.е.
ограничена, т.е.
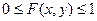
2. 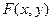 не убывает по каждому из своих аргументов при фиксированном другом, т.е.
не убывает по каждому из своих аргументов при фиксированном другом, т.е.
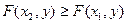 при
при 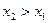
 при
при 
3. Если хотя бы один из аргументов обращается в 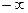 , то функция распределения
, то функция распределения 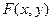 равна нулю, т.е.
равна нулю, т.е.
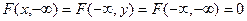
4. Если оба аргумента обращаются в  , то
, то 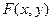 равна 1, т.е.
равна 1, т.е.
 .
.
5. Если один из аргументов обращается в  , то функция распределения системы случайных величин становится функцией распределения случайной величины, соответствующей другому элементу, т.е.
, то функция распределения системы случайных величин становится функцией распределения случайной величины, соответствующей другому элементу, т.е.
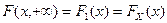 , , 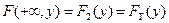 . .
| (6.4) |
6. 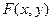 непрерывна слева по каждому из своих аргументов, т.е.
непрерывна слева по каждому из своих аргументов, т.е.
 ,
, 
Зная совместное распределение двух случайных величин X и Y, можно найти одномерные распределения этих случайных величин, но обратное, вообще говоря, неверно.
Отметим, что с геометрической точки зрения 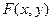 есть некоторая поверхность (ступенчатая для двумерной дискретной случайной величины), обладающая указанными свойствами.
есть некоторая поверхность (ступенчатая для двумерной дискретной случайной величины), обладающая указанными свойствами.
С помощью функции 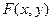 легко можно найти вероятность попадания случайной точки
легко можно найти вероятность попадания случайной точки  в прямоугольник D со сторонами, параллельными координатным осям:
в прямоугольник D со сторонами, параллельными координатным осям:
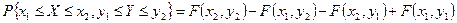 . .
| (6.5) |
Приведем геометрическое доказательство (рис. 6.3)
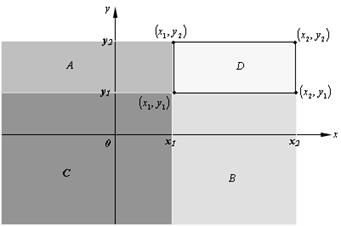
Рис. 6.3.
Здесь  - вероятность попадания случайной точки в область D,
- вероятность попадания случайной точки в область D, 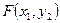 - в А,
- в А, 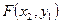 - в В,
- в В,  - в С (эту область дважды вычли, следует один раз прибавить).
- в С (эту область дважды вычли, следует один раз прибавить).
|
|
|
Пример 6.2. По таблицам распределения системы  компонент X и Y примера 6.1. найти
компонент X и Y примера 6.1. найти 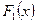 ,
, 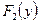 ,
, 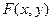 .
.
Решение:
Используя формулу (6.4), находим функцию распределения 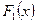 ,
, 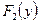 ,
,


Используя формулу (6.3.), находим функцию распределения 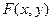 :
:

| 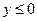
| 
| 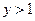
|
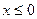
| |||
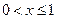
| 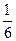
| 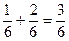
| |
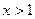
| 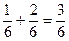
| 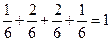
|
|
|
|


