 |
Многомерная (n-мерная) случайная величина (общие сведения)
|
|
|
|
Систему n случайных величин называют n- мерной (многомерной) случайной величиной или случайным вектором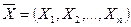 
.
Многомерная случайная величина есть функция элементарного события w: 
: каждому элементарному событию w ставится в соответствие n действительных чисел 
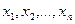- значения, принятые случайными величинами 
в результате опыта. Вектор 
называется реализацией случайного вектора .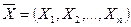
Закон распределения вероятностей n- мерной случайной величины задается ее функцией распределения
Функция распределения 
обладает такими же свойствами, как и функция распределения двух случайных величин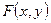 
. В частности: она принимает значения на отрезке [0, 1],
,
.
Плотность распределения системы n непрерывных случайных величин 
определяется равенством
.
При 
и
Вероятность попадания случайной точки в область D из n -мерного пространства выражается n -кратным интегралом
.
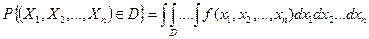Функция распределения 
выражается через плотность 
n -кратным интегралом
Необходимым и достаточным условием взаимной независимости n случайных величин является равенство:
,
а для n непрерывных случайных величин
.
Основными числовыми характеристиками многомерной случайной величины являются:
1. n математических ожиданий составляющих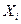 
, т.е.
2. n дисперсий составляющих 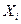, т.е.
,
при этом 
, 
.
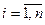3. n (n - 1) ковариаций, т.е.
, 
,
при этом 
, 
.
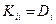Ковариации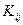 
образуют ковариационную матрицу
или 
Характеристическая функция и ее свойства
Наряду с функцией распределения, содержащей все сведения о случайной величине, для ее описания можно использовать так называемую характеристическую функцию. С ее помощью, в частности, упрощается задача нахождения распределения суммы независимых случайных величин, нахождения числовых характеристик случайных величин.
|
|
|
Характеристической функцией случайной величины X называется математическое ожидание случайной величины 
обозначается через 
или просто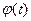 
. Таким образом, по определению
,
где t - параметр, 
- мнимая единица.
Для дискретной случайной величины X, принимающей значения x 1, x 2,… с вероятностями 
, 
, характеристическая функция определяется формулой
 ,
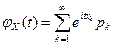| (6.43) |
для непрерывной случайной величины с плотностью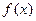 
- формулой
 .
| (6.44) |
Заметим, что:
1. Характеристическая функция непрерывной случайной величины есть преобразование Фурье от плотности ее распределения. Плотность 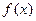выражается через 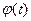обратным преобразованием Фурье:
.
2. Если случайная величина принимает целочисленные значения 0, 1, 2,..., то 
, где 
. Тогда
.
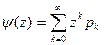Свойства характеристической функции:
1. Для всех 
имеет место неравенство
.
2. Если 
, где a, b - постоянные, то
.
3. Характеристическая функция суммы двух независимых случайных величин Х и Y равна произведению их характеристических функций
.
4. Если для некоторого k существует начальный момент k -го порядка случайной величины Х, т.е. 
, то существует k-я производная характеристической функции и ее значение при 
равно 
, умноженному на 
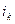, т.е.
.
Из свойства 4 следует,
.
Отсюда, как частный случай, можно получить:
,
,
 .
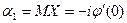
| (6.45) |
Характеристическая функция нормальной случайной величины
Согласно формуле (6.44), характеристическая функция случайной величины 
равна
.
Таким образом, 
, если .
Пример 6.9. Найти с помощью характеристической функции математическое ожидание и дисперсию случайной величины .
Решение:
Применим формулы (6.45):
, т.е. 
,
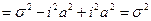, т.е. 
.
Получили известные нам результаты: 
- математическое ожидание, 
- среднее квадратическое отклонение. Эти параметры полностью определяют случайную величину, распределенную по нормальному закону.
|
|
|
|
|
|
