Алгоритм решения задачи

Статистика

Лабораторная работа № 1

Нормальное распределение. Критерии согласия

Построение нормального распределения по эмпирическим данным

 

Имея дело с эмпирическим распределением, можно предположить, что данному распределению соответствует определенная, характерная для него теоретическая кривая. Выдвинув гипотезу о той или иной форме распределения, стремятся описать эмпирический ряд с помощью математической модели, выражающей некоторый теоретический закон распределения. Среди различных кривых распределения особое место занимает нормальное распределение.

Нормальным N(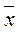,s) называют распределение непрерывной случайной величины x, если ее плотность распределения выражается формулой , где x – значение изучаемого признака

НОРМРАСП(x, 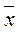, s, ложь)

Или

Интегральная функция непрерывной случайной величины распределенной нормально:

-

НОРМРАСП(x, 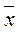, s, истина)= НОРМСТРАСП(НОРМАЛИЗАЦИЯ(x, 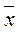, s))

 

Стандартное нормальное распределение N(0,1) при 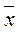=1, s=0

Плотность (дифференциальная функция)

- НОРМРАСП(x, 0, 1, ложь)

Интегральная функция

НОРМСТРАСП(x)= НОРМРАСП(x, 0, 1, истина)

 

Критерии согласия

 

Все предположения о характере того или иного распределения – это гипотезы, а не категорические утверждения. Поэтому должны быть подвергнуты статистической проверке с помощью показателей, которые называют критериями согласия.

Для установления теоретического закона распределения нужно определить:

1. вид закона распределения (определяется из теоретических предпосылок, опыта аналогичных предшествующих исследований, или на основании графического изображения эмпирического распределения)

2. параметры распределения (их заменяют наилучшими оценками по выборке)

Но, как бы хорошо ни был подобран теоретический закон распределения, между ним и эмпирическим распределением неизбежны расхождения.

Задача: определить, являются ли эти расхождения существенными (неслучайными), и теоретический закон распределения выбран неудачно, или расхождения несущественны, связаны лишь со случайными обстоятельствами, связанными с ограниченным числом наблюдений.

Для решения этой задачи используются случайные величины с известными законами распределения, называемые критерии согласия.

Рассмотрим три из них:

· Критерий Пирсона ()

· Критерий Романовского (С)

· Критерий Колмогорова (l)

Алгоритм решения задачи

Проверяется гипотеза Н₀: эмпирическое распределение подчиняется определенному теоретическому закону распределения.

Для этого выбирается случайная величина U (критерий согласия), характеризующая степень расхождения теоретического и эмпирического распределений. Закон распределения U при больших n известен и не зависит от эмпирического закона распределения.

1. найти u_набл. – фактически наблюдаемое в опыте расхождение теоретических и эмпирических распределений

2. зная закон распределения U, найти вероятность P(U>=u_набл.)=a по таблице распределения

3. вывод: если a мала, то H₀ отвергают, т. е. отклонения от теоретического закона распределения большие, чем полученные в опыте, практически невозможны. Следовательно, закон распределения для X выбран не верно. Если a не мала, то H₀ можно считать правдоподобной, т. е. не противоречащей опытным данным. Следовательно, расхождение между эмпирическими и теоретическими распределениями несущественно.

- критерий Пирсона

Пусть x₁, x₂, …, x_n – выборка из некоторой генеральной совокупности X (X - случайная величина), F(x) – предполагаемая функция теоретического распределения X.

F(x) – это интегральная функция распределения случайной величины X. Если в качестве теоретического распределения выбрано нормальное распределение со средним квадратическим отклонением s и мат. ожиданием а, то

- НОРМРАСП(x, а, s, истина)

Н₀: F(x) – это интегральная функция распределения случайной величины X.

 

1) На основании выборки построим интервальный вариационный ряд {D_i, f_i} i=1,…,m, где f_i – число элементов выборки, попавших в интервал D_i =[a_i, a_i+1); m – количество интервалов.

При этом f_i называют эмпирическими частотами,

 

2) Для каждого интервала D_i =[a_i, a_i+1) вычислим теоретические вероятности попадания случайной величины X в этот интервал pi=P(a_i<=X<=a_i+1)=F(a_i+1)-F(a_i)

n×p_i – называют теоретическими частотами

(n – число элементов в выборке, )

 

3) В качестве критерия согласия берем случайную величину . Известно, что она имеет распределение (распределение Пирсона) с числом степеней свободы k=m-r-1, где m – число интервалов вариационного ряда, r – число параметров теоретического распределения (Например, у нормального распределения два параметра: математическое ожидание и дисперсия, у распределения Пуассона один параметр - математическое ожидание).

Вычисляем

4) Для заданного уровня значимости a и числа степеней свободы k=m-r-1 по специально составленной таблице -распределения найдем . (статистическая функция Excel ХИ2ОБР(a;k))

5) Если 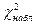> , то Н₀ отвергается, т. е. функция распределения F(x) выбрана неверно, если 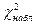<= , то Н₀ принимается, т. е. с вероятностью (1-a) можно утверждать, что расхождение между теоретическими и эмпирическими частотами случайны.

Замечания

1. Критерий Пирсона можно применять, только если n>30.

2. В каждом интервале D_i =[a_i, a_i+1) должно быть по крайней мере 5 наблюдений (f_i>=5), иначе соседние интервалы объединяют и m уменьшается.

 

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: