 |
Критерий Романовского
|
|
|
|
Основан на использовании критерия Пирсона, т. е. уже найденных 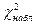 и числа степеней свободы k.
и числа степеней свободы k.
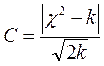
При С<3 расхождения между теоретическим и эмпирическим распределениями считаются случайными, если C>3, то неслучайными, и, следовательно, теоретическое распределение не может служить моделью для изучаемого эмпирического распределения.
Критерий Колмогорова
Дан вариационный ряд
| xi | ||||
| fi |
1. Строятся эмпирическая функция распределения Fn(x) 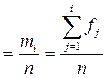 (накопленные частости, n – число элементов в выборке,
(накопленные частости, n – число элементов в выборке, 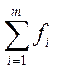 ) и предполагаемая теоретическая функция распределения F(x) (параметры закона распределения F(x) считаются известными)
) и предполагаемая теоретическая функция распределения F(x) (параметры закона распределения F(x) считаются известными)
2. Определяется мера расхождения между теоретическим и эмпирическим распределениями 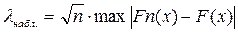 . Известно, что эта случайная величина распределена по закону Колмогорова.
. Известно, что эта случайная величина распределена по закону Колмогорова.
3. Для заданного уровня значимости a по таблице распределения Колмогорова найдем lкритич.(a)
| a | 0,4 | 0,3 | 0,2 | 0,1 | 0,05 | 0,025 | 0,01 | 0,005 | 0,001 | 0,0005 |
| l(a) | 0,89 | 0,97 | 1,07 | 1,22 | 1,36 | 1,48 | 1,63 | 1,73 | 1,95 | 2,03 |
4. Если lнабл. > lкритич., то Н0 отвергается, закон распределения F(x) выбран не верно,
если lнабл. <= lкритич., то Н0 не противоречит опытным данным.
Практическое задание
Задача 1
Рассчитать теоретические частоты ряда распределения на основании эмпирических данных о росте призывников, представленных в таблице.
| Группы призывников по росту, см. | Число призывников |
| 143 – 146 146 – 149 149 – 152 152 – 155 155 – 158 158 – 161 161 – 164 164 – 167 167 – 170 170 – 173 173 – 176 176 – 179 179 – 182 182 – 185 185 – 188 | |
| Итого |
Указания к решению
Выдвинув гипотезу о нормальном распределении, определим по эмпирическим данным параметры этой кривой. Для этого:
|
|
|
1. Найти средний рост призывников 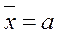
2. Найти среднее квадратическое отклонение 
3. Определить нормированное отклонение 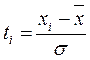 для каждого варианта xi (статистическая функция в Excel ti=НОРМАЛИЗАЦИЯ(xi,а,
для каждого варианта xi (статистическая функция в Excel ti=НОРМАЛИЗАЦИЯ(xi,а,  ))
))
4. По таблице нормального распределения найти значение функции 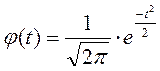 - НОРМРАСП(t, 0, 1, ложь)
- НОРМРАСП(t, 0, 1, ложь)
5. Определить теоретические частоты 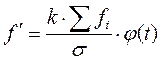 , где k – длина интервала (т. к. вариационный ряд имеет равные интервалы, то
, где k – длина интервала (т. к. вариационный ряд имеет равные интервалы, то 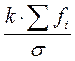 - это константа).
- это константа).
6. Сравнить на графике эмпирические 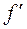 и теоретические
и теоретические 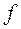 частоты.
частоты.
Задача 2
Для эмпирического распределения рабочих цеха по выработке по данным таблицы подобрать соответствующее теоретическое распределение и на уровне значимости 0,05 проверить гипотезу о согласованности двух распределений с помощью критерия «хи-квадрат».
| [xi,xi+1] | 94-100 | 100-106 | 106-112 | 112-118 | 118-124 | 124-130 | 130-136 | 136-142 |
| ni |
Указания к решению
1. Построить гистограмму распределения рабочих по выработке ([xi,xi+1]; wi=ni/n). По виду гистограммы убедитесь, что можно предположить нормальный закон распределения признака.
2. Параметры нормального закона математическое ожидание и дисперсия неизвестны, поэтому их заменяют на выборочную среднюю и «исправленную» выборочную дисперсию. Т. к. в данной задаче число наблюдений 100 достаточно велико, то вместо «исправленной» дисперсии можно взять обычную выборочную дисперсию. Найдите выборочную среднюю (а) и выборочную дисперсию ( ).
).
3. Выдвигается гипотеза: случайная величина X – выработка рабочих цеха - распределена нормально с параметрами а и  , т. е. X
, т. е. X 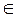 N(a,
N(a,  ). Для определения наблюдаемого значения критерия «хи-квадрат» удобно составить таблицу.
). Для определения наблюдаемого значения критерия «хи-квадрат» удобно составить таблицу.
| Интервал [xi,xi+1] | Эмпирические частоты, ni | Вероятности, pi | Теоретические частоты, npi | (ni-npi)2 | (ni-npi)2/npi |
Учитывая, что в рассматриваемом эмпирическом распределении частоты первого и последнего интервалов меньше 5, при использовании критерия «хи-квадрат» целесообразно объединить указанные интервалы с соседними.
|
|
|
Для расчета вероятностей pi попадания случайной величины X в интервал [xi,xi+1] используйте функцию Лапласа в соответствии со свойством нормального распределения:
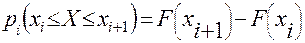 , где
, где
 - НОРМРАСП(x,
- НОРМРАСП(x, 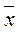 , s, истина)
, s, истина)
4. Найдите критическое значение критерия «хи-квадрат» по таблицам (в Excel статистическая функция ХИ2ОБР(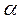 ,k=m-r-1), где m – новое число интервалов, после объединения, r – число параметров нормального закона распределения) и сделайте вывод о том, согласуется ли выбранный теоретический нормальный закон с опытными данными.
,k=m-r-1), где m – новое число интервалов, после объединения, r – число параметров нормального закона распределения) и сделайте вывод о том, согласуется ли выбранный теоретический нормальный закон с опытными данными.
Задача 3
Имеются следующие статистические данные о числе вызовов специализированных бригад скорой помощи в час в некотором населенном пункте в течение 300 часов. Подобрать соответствующее теоретическое распределение и на уровне значимости 0,05 проверить гипотезу о согласованности двух распределений с помощью критерия «хи-квадрат».
| Число вызовов в час, xi | |||||||||
| Частота, ni |
Указания к решению
1. Построить полигон частот дискретной случайной величины X.
2. Вычислить выборочную среднюю и выборочную дисперсию.
3. Выдвигаем гипотезу: случайная величина X – число вызовов скорой помощи в час – распределена по закону Пуассона с параметром 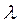 равным выборочной средней.
равным выборочной средней.
Причины выбора в качестве теоретического закона распределение Пуассона:
· вызов скорой помощи для каждого жителя – событие в целом достаточно редкое
· по виду полигон частот дискретной случайной величины X напоминает полигон пуассоновского распределения вероятностей при небольших значениях 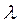 .
.
· для распределения Пуассона характерно равенство дисперсии и среднего значения, а в пункте 2 мы получили приближенно равные выборочную среднюю и выборочную дисперсию.
4. Для определения наблюдаемого значения критерия «хи-квадрат» составим таблицу (см. задачу 2). Вероятность значений случайной величины X найдем по формуле 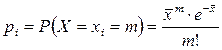 Для этого воспользуйтесь статистической функцией ПУАССОН(
Для этого воспользуйтесь статистической функцией ПУАССОН(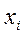 ;
; 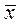 ; ложь). При вычислении наблюдаемого значения критерия «хи-квадрат» объедините интервалы с частотой меньшей 5 с соседними интервалами.
; ложь). При вычислении наблюдаемого значения критерия «хи-квадрат» объедините интервалы с частотой меньшей 5 с соседними интервалами.
|
|
|
5. Найдите критическое значение критерия «хи-квадрат» по таблицам (в Excel статистическая функция ХИ2ОБР(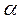 ,k=m-r-1), где m – новое число интервалов, после объединения, r – число параметров распределения Пуассона (r=1)) и сделайте вывод о том, согласуется ли выбранный теоретический закон с опытными данными.
,k=m-r-1), где m – новое число интервалов, после объединения, r – число параметров распределения Пуассона (r=1)) и сделайте вывод о том, согласуется ли выбранный теоретический закон с опытными данными.
Задача 4
По данным задачи 2 с помощью критерия Колмогорова на уровне значимости 0,05 проверить гипотезу о том, что случайная величина X – выработка рабочих предприятия – имеет нормальный закон распределения с параметрами а=119,2; 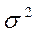 =87,48, т. е. N(119,2; 87,48).
=87,48, т. е. N(119,2; 87,48).
Указания к решению:
1. В качестве вариант возьмем среднее значение в каждом интервале данного в задаче интервального вариационного ряда.
2. Значение эмпирической функции распределения Fn(x) вычислим как накопленные частости 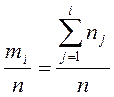
3. Для построения теоретической функции распределения для нормального закона с параметрами а=119,2; 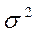 =87,48 F(x) воспользуйтесь встроенной статистической функцией НОРМРАСП(xi;119,2;9,35;истина)
=87,48 F(x) воспользуйтесь встроенной статистической функцией НОРМРАСП(xi;119,2;9,35;истина)
4. Для вычислений заполните таблицу
| xi | ni | mi | Fn(x) | F(x) | |Fn(x)-F(x)| |
Для определения наблюдаемого значения критерия Колмогорова вычислите значение 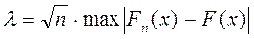
5. Найдите критическое значение критерия Колмогорова по таблицам для уровня значимости 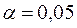 и сделайте вывод о том, согласуется ли выбранный теоретический закон с опытными данными.
и сделайте вывод о том, согласуется ли выбранный теоретический закон с опытными данными.
Задача 5
По данным задачи 1 с помощью критериев
a) Пирсона
b) Романовского
c) Колмогорова
на уровне значимости 0,05 проверить гипотезу о распределении призывников по росту по нормальному закону распределения.
|
|
|


