 |
Моделирование и анализ режимов работы
|
|
|
|
Простейших схем электрических сетей
Векторная диаграмма ЛЭП
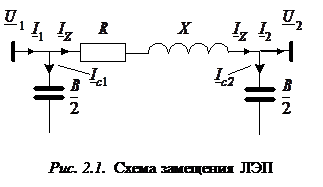 Рассмотрим соотношения между токами и напряжениями в ЛЭП, представленной П-образной схемой замещения (рис. 2.1), в которой не учитываются активные поперечные проводимости. Здесь и в дальнейшем рассматриваются симметричные режимы работы электрических сетей и поэтому для простоты изображается схема замещения только одной фазы трехфазной сети. На схеме обозначены комплексные действующие значения токов и напряжения по концам линии и в элементах схемы замещения: I Z – ток в продольном сопротивлении линии Z = R + jX; I C 1 I C 2 – токи в поперечных емкостных проводимостях; эти токи называют зарядными токами в конце и в начале схемы замещения линии. Направления токов, показанные на рис. 1.2, являются условными, так как, во-первых, синусоидальные переменные токи фаз меняются по величине и направлению, и, во-вторых, это действующие значения, изображаемые в виде векторов на комплексной плоскости, которые в общем случае могут иметь различные направления (расположения). Условимся связывать указываемые на схеме направления токов с направлением потока активной мощности (потока энергии), тогда при совмещении напряжения в точке, через которую протекает ток, с действительной осью, имеем – для индуктивного характера потока мощности
Рассмотрим соотношения между токами и напряжениями в ЛЭП, представленной П-образной схемой замещения (рис. 2.1), в которой не учитываются активные поперечные проводимости. Здесь и в дальнейшем рассматриваются симметричные режимы работы электрических сетей и поэтому для простоты изображается схема замещения только одной фазы трехфазной сети. На схеме обозначены комплексные действующие значения токов и напряжения по концам линии и в элементах схемы замещения: I Z – ток в продольном сопротивлении линии Z = R + jX; I C 1 I C 2 – токи в поперечных емкостных проводимостях; эти токи называют зарядными токами в конце и в начале схемы замещения линии. Направления токов, показанные на рис. 1.2, являются условными, так как, во-первых, синусоидальные переменные токи фаз меняются по величине и направлению, и, во-вторых, это действующие значения, изображаемые в виде векторов на комплексной плоскости, которые в общем случае могут иметь различные направления (расположения). Условимся связывать указываемые на схеме направления токов с направлением потока активной мощности (потока энергии), тогда при совмещении напряжения в точке, через которую протекает ток, с действительной осью, имеем – для индуктивного характера потока мощности
 (2.1)
(2.1)
и для емкостного характера
 , (2.2)
, (2.2)
где вектор  всегда будет направлен по вещественной оси в положительном направлении, а вектор на мнимой оси - jI или jI определяет отставание вектора тока I от напряжения U для индуктивного и опережение для емкостного характера мощности.
всегда будет направлен по вещественной оси в положительном направлении, а вектор на мнимой оси - jI или jI определяет отставание вектора тока I от напряжения U для индуктивного и опережение для емкостного характера мощности.
По первому закону Кирхгофа имеем соотношения для токов в схеме замещения
|
|
|
 и
и  . (2.3)
. (2.3)
Второй закон Кирхгофа дает
 , (2.4)
, (2.4)
где D U - падение напряжения на продольном сопротивлении Z:
 . (2.5)
. (2.5)
Зарядные токи определяются по формулам:
 и
и  , (2.6)
, (2.6)
Подставляя выражения (2.5) в (2.4) и (2.6) в (2.3), будем иметь
 (2.7)
(2.7)
и после подстановки U 1 в выражение для I 1 и некоторых преобразований получим
 (2.8)
(2.8)
Полученные линейные соотношения являются уравнениями четырехполюсника и позволяют вычислить напряжение и ток в начале ЛЭП по известным напряжению и току в конце ЛЭП. Любое другое парное сочетание известных параметров режима линии { U 1, I 1}, { U 1, I 2}, { U 2, I 1} требует решения линейных уравнений (2.8) относительно двух других неизвестных параметров.
Построим векторную диаграмму ЛЭП при известных напряжении и токе в конце линии.
Для индуктивного характера нагрузки в конце ЛЭП имеем отстающий ток на угол j2 :
 (2.9)
(2.9)
Здесь U 2 совмещено с действительной осью комплексной системы координат U 2 = U 2.
Порядок (алгоритм) построения векторной диаграммы следующий.
1. Откладываем по вещественной оси вектор U 2 и отстающий от него на угол j2 вектор I 2 (рис. 2.2).

Рис. 2.2. Векторная диаграмма ЛЭП
2. Строим вектор тока в линии I Z как сумму векторов I 2 и I C 2. Ток I C 2 опережает U 2 на 90°.
3. Строим вектор напряжения U 1 как сумму векторов U 2 и D U = D U R + j D U X, причем вектор падения напряжения на активном сопротивлении D U R совпадает по фазе с током I Z, а вектор падения напряжения на индуктивном сопротивлении D U X опережает ток I Z на 90°. Угол между векторами напряжений U 1 и U 2 обозначается буквой d.
4. Строим вектор тока в начале линии I 1 как сумму тока в линии I Z и I C 1, который опережает U 1 на 90°.
Из построенной векторной диаграммы можно сделать следующий вывод: при передаче мощности по ЛЭП и индуктивном характере нагрузки вектор напряжения источника опережает вектор напряжения приемника на угол d и величина вектора напряжения источника оказывается больше величины вектора напряжения приемника.
|
|
|
Баланс мощностей в ЛЭП
Из закона сохранения энергии следует, что для любой электрической цепи соблюдается баланс активных мощностей: активная мощность всех источников равна активной мощности, потребляемой всеми элементами цепи и приемниками. То же самое справедливо и для реактивных мощностей: сумма отдаваемых реактивных мощностей равна сумме потребляемых реактивных мощностей. Можно также записать баланс для комплексных мощностей: сумма комплексных мощностей, потребляемых всеми ветвями цепи с учетом источников и приемников, равна нулю.
 Рис.2.3. Мощности в схеме
замещения ЛЭП
Рис.2.3. Мощности в схеме
замещения ЛЭП
|
В ЛЭП имеются источник – мощность, отдаваемая энергосистемой в линию, приемник – мощность, отдаваемая линией в энергосистему, и три ветви: одна с активно-индуктивным сопротивлением и две с емкостями. Запишем баланс мощностей для ЛЭП
(рис. 2.3)
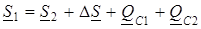 , (2.10)
, (2.10)
где S 1 – мощность в начале линии (источника); S 2 – мощность в конце линии (приемника); D S – потери мощности в продольном сопротивлении линии;
Q C 1 и Q C 2 – мощности в поперечных элементах – емкостных проводимостях схемы замещения ЛЭП, их называют зарядными мощностями в конце и в начале линии.
Мощность в начале линии S 1 часто отождествляют с мощностью пункта питания S ПП, к которому присоединена линия, но это справедливо лишь в том случае, когда к этому пункту питания больше не присоединены никакие другие линии или электроприемники.
Мощность в конце линии S 2 будет равна мощности нагрузки S Н, которая имеется на шинах в конце линии, но только в том случае, если к этим шинам не присоединены какие-либо другие элементы сети (линии, трансформаторы и пр.). В некоторых случаях нагрузкой в конце линии считается суммарная мощность всех ветвей, по которым идет отдача мощности от линии.
Потери мощности в продольном сопротивлении линии в схеме замещения определяются через ток I Z (см. рис. 2.1)
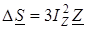 . (2.11)
. (2.11)
Ток I Z может быть определен как через мощность и напряжение в конце, так и через мощность и напряжение в начале сопротивления Z.
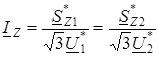 . (2.12)
. (2.12)
При подстановке (2.12) в (2.11) получается формула для расчета потерь мощности через потоки мощности в линии:
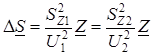 . (2.13)
. (2.13)
Раздельно потери активной и реактивной мощности, вычисляемые по данным в начале и в конце сопротивления с учетом того, что S 2 = P 2 + Q 2 и Z = R + jX, определяются по формулам:
|
|
|
 и
и  (2.14)
(2.14)
и
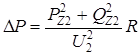 и
и  . (2.15)
. (2.15)
Мощности в емкостных проводимостях (поперечных ветвях схемы замещения) определяются по формулам:
 и
и 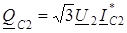 (2.16)
(2.16)
Зарядные токи в (2.16) определяются через напряжения на емкостных элементах схемы замещения
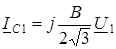 и
и 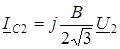 (2.17)
(2.17)
Подстановка (2.17) в (2.16) дает выражение для зарядных мощностей в начале и конце схемы замещения ЛЭП:
 и
и  . (2.18)
. (2.18)
Знак минус в (2.18) говорит о том, что в комплексной системе координат векторы зарядных мощностей ориентированы в отрицательном направлении на мнимой оси.
Важно понимать, что знаки в комплексных величинах мощностей определяются также указанными направлениями потоков мощности на электрической схеме. Исходя из того, что мы приняли положительное направление потока мощности в направлении передачи энергии (активной мощности), и с учетом направлений потоков мощностей на схеме рис. 2.3 векторы потоков реактивной мощности будут «положительны» (направлены по положительной мнимой полуоси), если реактивная мощность индуктивного характера, и «отрицательны» (направлены по отрицательной полуоси), если реактивная мощность емкостного характера. Поэтому в отношении зарядных мощностей начала и конца схемы замещения ЛЭП говорят, что это реактивные мощности генерации и что линия наряду с потерями также генерирует реактивную мощность.
Сумму Q C 1 и Q C 2 называют зарядной мощностью линии. Потери реактивной мощности D Q и зарядная мощность QC = QC 1 + QC 2 линии соизмеримы между собой и при определенных условиях могут быть равны друг другу.
|
|
|


