Построение прямой аппроксимирующей свойства тренда с помощью МНК

Реферат

 

В отчете содержится: 24 формулы, 10 рисунков.

Ключевые слова: тренд прогноза, логнормальный закон, шум, критерий χ²-Пирсона, проверка гипотез, оценки расхождения.

Целью данной работы было исследование точности прогнозирования случайного процесса с использованием метода наименьших квадратов. Для этого проводился машинный эксперимент с использованием программы Mathcad 14. Основой для построения случайной функции являлась линейная функция, на которую был наложен случайный шум, распределенный по логнормальному закону с параметрами М[шума]=0 (математическое ожидание шума) и D[шума]=D (дисперсия шума). После чего полученная случайная функция аппроксимировалась линейным трендом, а также исследовалось расхождение между трендом и прогнозом с последующей оценкой близости распределения расхождений наблюдений и распределения сгенерированного шума по критерию χ²-Пирсона.

Определения и формулы

 

Математическим ожиданием P(ξ=x_i) дискретной случайной величины ξ называется сумма парных произведений всех возможных значений случайной величины на соответствующие им вероятности, т.е:

 

,                                    (1)

 

где х_i – значение случайной величины, p_i – вероятность этого значения, n – общее число значений.

Математическим ожиданием P(ξ=x_i) непрерывной случайной величины ξ с плотностью распределения φ(x) называется число, определяемое равенством:

 

,                                     (2)

 

где φ(x) – плотность распределения случайной величины.

Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата ее отклонения от ее математического ожидания:

 

                             (3)

 

Для непрерывной случайной величины формула (3) будет представлена в виде:

                         (4)

 

Среднее квадратичное отклонение(СКО) – это статистическая величина, описывающая разброс значений изучаемой величины вокруг ее ожидаемого значения:

 

                                        (5)

 

В математической статистике оперируют оценками числовых характеристик, которые ищутся по случайной выборке. В отличие от самих параметров, оценки содержат элемент случайности. К оценкам параметров предъявляют определенные требования:

а) состоятельность – оценка, соответствующая этому требованию, с увеличением объема выборки сходится по вероятности к самому параметру;

б) несмещенность – математическое ожидание такой оценки равно оцениваемому параметру;

в) эффективность – дисперсия эффективной оценки минимальна.

Оценка математического ожидания ищется по формуле:

 

,                                      (6)

 

где n – объем случайной выборки. Оценка, вычисленная по формуле (6), называется так же статистическим средним.

Оценка дисперсии вычисляется по формуле:

 

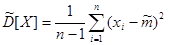,                          (7)

где m – оценка математического ожидания случайной величины.

Оценка С.К.О. вычисляется по формуле:

 

,                              (8)

 

т.е. корень квадратный из оценки дисперсии.

При генерации шума мы используем два закона: нормальное и логнормальное распределение.

Нормальный закон: Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности:

 

 (9)

 

Функция распределения F(x) в рассматриваемом случае принимает вид:

 

 (10)

 

График 1 – распределение плотности вероятности нормального закона:

 

Рисунок 1. Плотность вероятности нормального закона

 

Говорят, что случайная величина X имеет логнормальное распределение с параметрами μ, σ, если X = exp(Y), где Y имеет нормальное распределение с параметрами μ, σ. Случайная величина с логнормальным распределением является непрерывной, и принимает только положительные значения. Графики плотности (привязан к левой вертикальной оси ординат) и функции (привязан к правой оси ординат) логнормального распределения с параметрами μ = 0, σ = 0.7 приведен на следующем рисунке 2:

 

Рисунок 2. Логнормальное распределение

Плотность распределения логнормального закона:

 

 (11)

 

Функция распределения:

 

  (12)

Для определения степени расхождения теоретической кривой и статистических данных пользуются критериями согласия. Наиболее часто для проверки гипотезы о законе распределения используются 2 критерия: критерий λ-Колмогорова и критерий χ²-Пирсона.

Расчетное значение для критерия χ²-Пирсона вычисляется по формуле:

 

, где (13)

 –                          (14)

 

вероятность попадания в интервал разбиения с номером i, m_i – число значений функции в интервале разбиения, m, σ – математическое ожидание и с.к.о. случайной величины X, Φ^* – интеграл вероятностей.

Чтобы определить функциональную зависимость между величинами по результатам наблюдений, используем метод наименьших квадратов (МНК):

Пусть из опыта получены точки:

 

x1, y1,                

xn, yn

 

Требуется найти уравнение прямой y=ax+b (15), наилучшим образом согласующейся с опытными точками. Пусть мы нашли такую прямую. Обозначим через δ_i расстояние опытной точки от этой прямой (измеренное параллельно оси y).

Из уравнения (15) следует, что:

 

 (16)

 

Чем меньше числа по абсолютной величине, тем лучше подобрана прямая (15). В качестве характеристики точности подбора прямой (15) можно принять сумму квадратов:

 

 (17)

 

Покажем, как можно подобрать прямую (15) так, чтобы сумма квадратов S была минимальной. Из уравнений (16) и (17) получаем:

 

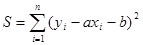 (18)

 

Условия минимума S будут равны для линейной функции:

 

(19)

  (20)

 

Уравнения (19) и (20) можно записать в таком виде:

(21)

  (22)

 

По уравнениям (21) и (22) легко найти a и b по опытным значениям x_i и y_i. Прямая (15), определяемая уравнениями (21) и (22), называется прямой, полученной по методу наименьших квадратов (этим названием подчеркивается то, что сумма квадратов S имеет минимум). Уравнения (21) и (22), из которых определяется прямая (15), называются нормальными уравнениями.

 

Введение

 

В качестве тренда процесса был выбран линейный тренд вида

 

Y= at+b,                                      (23)

 

где а =1, b =2. Тренд процесса показан на рисунке 3.

 

Рисунок 3. График тренда

 

График прямой с учетом сгенерированного шума по логнормальному закону выглядит так:.

 

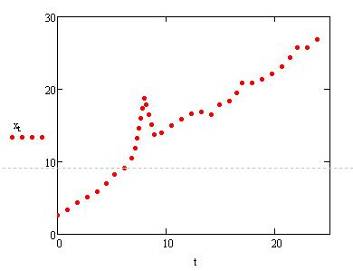
Рисунок 4. График прямой с учетом шума.

Наша задача в курсовом проекте заключается в определении насколько сильно шум влияет на прогнозирование. Для этого мы определяем расхождения между трендом и прогнозом и оцениваем степень расхождения из-за шума по критерию Пирсона

Построение прямой аппроксимирующей свойства тренда с помощью МНК

 

Наша ошибка сгенерирована по логнормальному закону с математическим ожиданием равным 0 и дисперсией равной 1. Гистограмма распределения шума представлена на рисунке 5.

 

Рисунок 5. (Гистограмма распределения значений шума по интервалам).

 

С помощью формул (21) и (22) вычислим коэффициенты линейного уравнения тренда с учетом шума с помощью метода МНК:

 

 

 

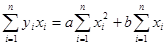
По найденным коэффициентам строим график прямой, которая аппроксимирует основные свойства линейного тренда. График показан на рисунке 6:

Рисунок 6. (Прямая, построенная по методу наименьших квадратов).

 

12	Поделиться:

Воспользуйтесь поиском по сайту: