Анализ результатов эксперимента

 

Полученные значения расхождений Δ представим в виде гистограммы и эмпирической функции по интервалам на рисунке 9:

 

 

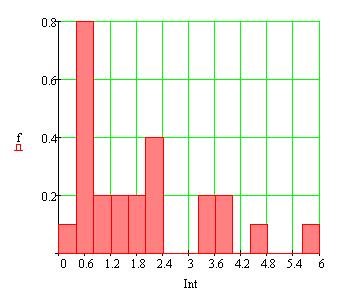
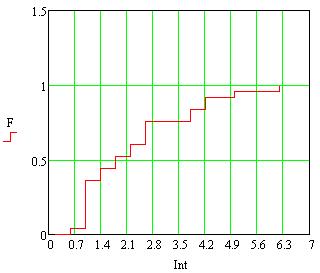
Рисунок 9. (На рисунке представлены гистограмма распределения значений Δ по интервалам, а так же график функции распределения Δ).

 

Из рисунков видно, что закон Δ больше всего похож на логнормальный, поэтому для сравнения оценки расхождения распределения сгенерируем выборку объемом в 25 (а так же выборки объемом 100, 500 и 1500) по логнормальному закону с математическим ожиданием 0 и дисперсией 1 и вычислим параметры.

 

Сгенерированная выборка:

N	1	2	3	4	5	6	7	8	9	10	11	12	13
xL	3.532	0.494	1.002	3.027	2.441	0.055	0.116	1.229	0.54	0.302	1.104	2.161	1.358
N	14	15	16	17	18	19	20	21	22	23	24	25
xL	1.011	0.466	0.664	0.51	0.876	2.768	1.198	1.671	2.095	0.984	1.322	1.176

 

Оценки математического ожидания, дисперсии и СКО рассчитаем по формулам:

 

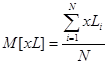
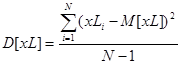
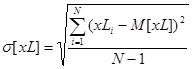 (24)

M[xL]=1.284; D[xL]=0.848; σ[xL]=0.921

 

На рисунке 10 показана гистограмма и эмпирическая функция по сгенерированной выборке:

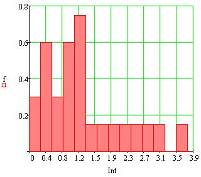
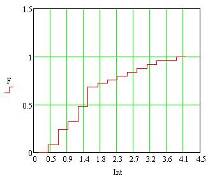
Рисунок 10. (На рисунке показанная функций распределения, а так же гистограмма распределения значений по интервалам для случайной величины, распределенной по логнормальному закону распределения с выборкой 25).

4. Проверка близости по критерию χ2 Пирсона закона распределения расхождений наблюдений и сгенерированного шума

 

Проверим насколько расходятся значения при прогнозе и по тренду. Для этого определяются интервалы разбиения расхождений прогноза и вычисление вероятностей попасть в интервал по логнормальному закону с математическим ожиданием равным 0 и дисперсией 1 по формуле (9).

Далее посчитаем сумму квадратов расхождения между частотами и вероятностью попасть в интервал логнормального закона:

 

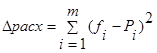 (25)

 

На основе суммы квадратов расхождения Δрасх можно посчитать расчетное значение критерия согласия Пирсона:

 

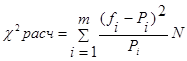 (26)

 

На полигоне частот (рисунок 11) показаны значения частоты распределения чисел по интервалам и вероятностей попадания в эти интервалы.

Теоретическое значение критического значения критерия Пирсона при уровне значимости α=0.1 и числом степеней свободы r=m-1 рассчитаем по формуле (11).

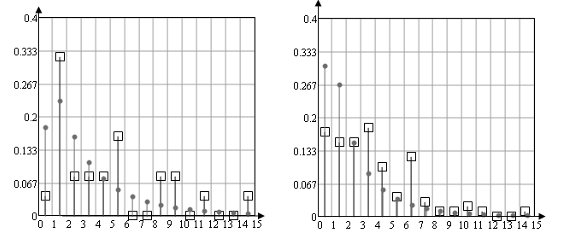
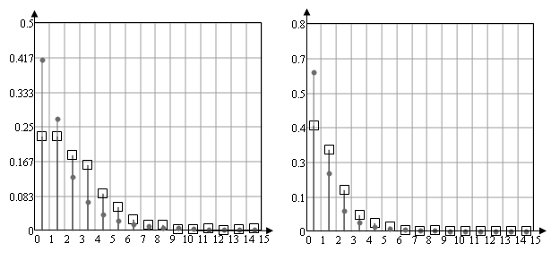
Рисунок 11.

 

(На рисунке показано расхождения между частотой попадания случайной величины в интервал и функцией распределения для попадания в этот интервал для выборок 25, 100, 500 и 1500. Случайная величина распределена по логнормальному закону распределения).

 

Ставится гипотеза: H₀ – расхождение между прогнозом и трендом распределено по логнормальному закону

Количество экспериментов	Критическое значение χ²	Эмпирическое значение χ²	Решение
25	21.064	26.135	Гипотеза H0 отвергается
100	21.064	65.549	Гипотеза H0 отвергается
500	21.064	102.753	Гипотеза H0 отвергается
1500	21.064	241.778	Гипотеза H0 отвергается

 

Так как в результате опытов выяснилось, что расхождение с ожидаемыми результатами велико, то в таком случае проверим правильность работы нашей модели, сгенерировав шум по нормальному закону распределения и проанализируем результаты.

 

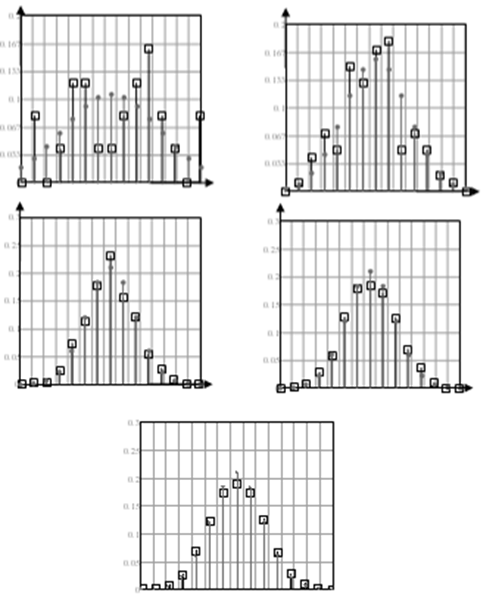
Рисунок 12.

(На рисунке показано расхождения между частотой попадания случайной величины в интервал и функцией распределения для попадания в этот интервал для выборок 25, 100, 500, 1500 и 10000. Случайная величина распределена по нормальному закону распределения, для проверки взято теоретическое распределение с параметрами m_x=0 и D_x=1).

Поставим гипотезу: H₀ – расхождение между прогнозом и трендом распределено по нормальному закону распределения (с параметрами m_x=0 и D_x=1).

 

Количество экспериментов	Критическое значение χ²	Эмпирическое значение χ²	Решение
25	21.064	14.865	Гипотеза H0 принимается
100	21.064	10.266	Гипотеза H0 принимается
500	21.064	9.161	Гипотеза H0 принимается
1500	21.064	32.575	Гипотеза H0 отвергается
10000	21.064	114.286	Гипотеза H0 отвергается

 

Отвержение гипотезы H₀ о распределении случайной величины по нормальному закону при выборках 1500 и 10000 с параметрами m_x=0 и D_x=1 свидетельствует об изменении параметров закона распределения (т.к. нормальный закон устойчив к линейным преобразованиям и сам закон не меняется), что является следствием линейных преобразований. Используем для проверки гипотезы о законе распределения с помощью критерия Пирсона теоретический закон распределения с дисперсией, равной оценке дисперсии отклонения прогноза от тренда, вычисленной по методу моментов.

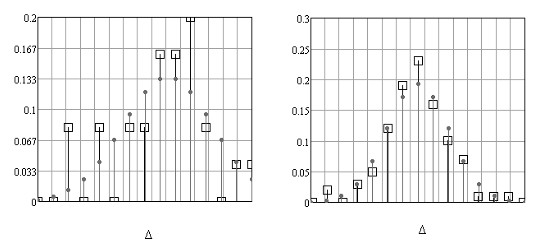
Рисунок 13.

 

(На рисунке показано расхождения между частотой попадания случайной величины в интервал и функцией распределения для попадания в этот интервал для выборок 25, 100, 500, 1500 и 10000. Случайная величина распределена по нормальному закону распределения, для проверки взято теоретическое распределение с параметрами m_x=0 и D_x= D_Δ (D_Δ =1.343; 1.149; 1,235; 1.158; 1.141)).

Поставим новую гипотезу: H₀ – расхождение между прогнозом и трендом распределено по нормальному закону распределения (с параметрами m_x=0 и D_x=D_Δ).

Количество экспериментов	Критическое значение χ²	Эмпирическое значение χ²	Решение
25	21.064	12.251	Гипотеза H0 принимается
100	21.064	11.616	Гипотеза H0 принимается
500	21.064	11.503	Гипотеза H0 принимается
1500	21.064	14.31	Гипотеза H0 принимается
10000	21.064	11.275	Гипотеза H0 принимается

12	Поделиться:

Воспользуйтесь поиском по сайту: