 |
Оценка качества регрессионного уравнения.
|
|
|
|
Оценка качества регрессионного уравнения производится с помощью использования ряда критериев:
1. Функция логарифмического правдоподобия.
2. Информационный критерий Акаике.
3. Критерий Байеса-шварца
4. Критерий Ханаана-Квина.
Функция логарифмического правдоподобия. Качество приближения регрессионной модели оценивается при помощи функции подобия. Мерой правдоподобия служит отрицательное удвоенное значение логарифма этой функции (-2LL). В качестве начального значения для -2LL применяется значение, которое получается для регрессионной модели, содержащей только константы. Если после добавления переменной влияния х1 значение -2LL снижается, то это означает улучшение качества регрессии.
Информационный критерий Акаике. Этот критерий близок к критерию правдоподобия, но дополнительно учитывает количество наблюдений и количество переменных. Критерий Акаике является эвристической попыткой свести в один показатель два требования: уменьшение числа параметров модели и качество подгонки модели. Согласно этому критерию из двух моделей следует выбрать модель с наименьшим значением критерия.
Критерий Байеса-Шварца. В статистике, для того чтобы описать определенный набор данных, можно использовать либо непараметрические, либо параметрические методы. При использовании параметрических методов, существует множество различных моделей-«кандидатов» с разным числом параметров для описания набора данных.Число параметров в модели очень важно. Правдоподобие обучающих данных увеличивается с увеличением числа параметров в модели, но, в случае слишком большого числа параметров, может возникнуть проблема «перетренировки» данных. Для того чтобы подобное не возникало, необходимо использовать информационный критерий Байеса (параметрический метод) – статистический метод для выбора модели, вычисляемый по следующей формуле:
|
|
|
(18)
Если оцениваются две модели, то выбирается та, у которой ниже значение информационного критерия Байеса.
Критерий Ханана-Квина. Согласно критерию Ханана-Квина, количество информации, содержащейся в модели, ‑ это расстояние от «истинной» модели и оно измеряется логарифмической функцией правдоподобия. Цель данного информационного критерия – обеспечить меру информации, которая достигала бы баланса между этой меры критерия согласия и неизвестными условиями модели. Методика работы различных информационных критериев варьируется при поиске этого баланса.
Для линейной регрессии с одним фактором формула данного показателя выглядит следующим образом:
(19)
2 ПОРЯДОК ПОСТРОЕНИЯ ЭКОНОМИКО-МАТЕМАТИЧЕСКОЙ МОДЕЛИ С ПОМОЩЬЮ МЕТОДА РЕГРЕССИОННОГО АНАЛИЗА
Задачи математического моделирования экономических показателей часто возникают в экономике и задачах управления. Получаемые модели используют для прогнозирования состояния процессов, более глубокого их изучения и управления ими.
Алгоритм построения однофакторной регрессионной модели:
1. Постановка задачи, сбор количественных показателей.
Например, при анализе прибыли предприятия могут быть построены следующие модели:
- зависимость прибыли от объема производства;
- зависимость прибыли от товарооборота;
- зависимость прибыли от численности персонала.
Для построения таких моделей необходимо подготовить данные об оценках соответствующих величин в денежном или натуральном выражении. Периодичность сбора этих данных может быть: ежемесячной, ежеквартальной, ежегодной.
2. Установление априорной зависимости между показателями. После подготовки данных необходимо провести их первичный анализ: оценить визуально зависимость между данными путем построения графика зависимости, рассчитать коэффициент корреляции. Такой анализ позволит сделать предположение о виде модели, коэффициенты которой необходимо оценить.
|
|
|
3. Оценка моделей методом наименьших квадратов, анализ полученных результатов.
В самом общем виде однофакторная регрессионная модель может быть представлена в виде:
(20)
Либо без константы:
(21)
При проведении анализа регрессионной модели необходимо проанализировать:
· ее точность (сумма квадратов ошибок и средняя ошибка должна стремиться к нулю, коэффициент детерминации – к единице);
· значимость коэффициентов регрессионного уравнения (коэффициенты должны быть значимы);
· адекватность регрессионного уравнения;
· качество регрессионной модели по критериям логарифмического правдоподобия, Акаике, Байеса-Шварца, Ханаана-Квина.
Экономический смысл параметров уравнения линейной парной регрессии: Параметр 
показывает среднее изменение результата y с изменением фактора x на единицу. Параметр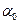 
=y, когда x=0. Если x не может быть равен 0, то 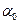не имеет экономического смысла. В противном случае, параметр 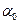означает начальное значение у. (Например, если построена модель линейной регрессии зависимости затрат от объема производства, то параметр 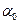будет означать значение постоянных издержек).
4. Третий этап заключается в выборе лучшей модели из полученных вариантов. На этом этапе выбирают лучшую модель с помощью нескольких статистических параметров. Они позволяют оценить по отдельности значимость коэффициентов математической модели в статистическом смысле, определить интегральную ошибку модели по отношению к исходному временному ряду, установить наличие корреляции между значениями ошибки модели, а также определить степень адекватности модели процессу в целом.
Для выбора наилучшей модели используют следующие параметры:
- статистика Стьюдента, определяющая значимость каждого коэффициента регрессии в статистическом смысле;
- статистика Фишера, определяющая степень адекватности модели в целом.
- коэффициент множественной детерминации 
(для лучшей модели должен приближаться к 1;
|
|
|
- сумма квадратов ошибок модели 
(из возможных вариантов необходимо выбрать ту модель, для которой сумма квадратов ошибок и средняя ошибка принимают минимальное значение);
- информационный критерий Акаике (AIC);
- критерий Байеса-Шварца (BSC);
- критерий Ханаана-Квина.
3 ОДНОФАКТОРНЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ В СИСТЕМЕ «GRETL»
Для проведения регрессионного анализа необходимо:
1) Ввести данные.
2) Вызвать меню Model >Ordinary least squares – позволяет выполнить простую регрессию (построение зависимости между откликом и переменной), и заполнить следующие ячейки:
Dependent variable – зависимая переменная, или переменная отклика;
Independent variable – независимые переменные.
Рисунок 3.1 – Диалоговое окно команды Model >Ordinary least squares
В результате расчетов модели линейной регрессии в окне результатов появляются следующие данные (см. рисунок 3.2.).
Рисунок 3.2 – Результаты расчетов однофакторной регрессионной модели
Приведенные ниже результаты показывают коэффициенты уравнения линейной модели и их значимость:
| coefficient | std. error | t-ratio | p-value | |
| ----------------------------------------------------------------- | ||||
| const | -33,7039 | 22,0549 | -1,528 | 0,1330 |
| x1 | 3,56472 | 0,165402 | 21,55 | 2,49E-026 *** |
Ниже приводится расшифровка полученных результатов.
coefficient – коэффициент линейной регрессии (const 
– константы, 
-x1 – фактора), исходя из этих коэффициентов можем составить уравнение регрессии:
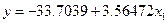
std. error – среднеквадратическое отклонение коэффициента линейной регрессии
t-ratio – t-критерий Стъюдента, который рассчитывается для проверки гипотезы о значимости коэффициента регрессионного уравнения. Гипотезы, которые проверяются:
p-value – значение р (вероятность ошибки). Если 
, то принимается нулевая гипотеза и коэффициент регрессии не значим, в противном случае, нулевая гипотеза отвергается и принимается альтернативная, т.е. коэффициент регрессии значим.
Mean of dependent variable – среднее значение зависимой переменной (у).
Standard deviation of dep. var. – среднеквадратическое отклонение зависимой переменной (у).
Sum of squared residuals – сумма квадратов ошибок.
Standard error of the regression – стандартная ошибка регрессии.
|
|
|
Сумма квадратов ошибок и стандартная ошибка регрессии отражают степень разброса фактических значений от расчетных, полученных по модели, чем меньше сумма квадратов ошибок и стандартная ошибка регрессии, тем точнее модель.
Unadjusted R-squared и Adjusted R-squared – коэффициенты детерминации без учета степеней свободи и с учетом степеней свободы.
Degrees of freedom - Степени свободы
Log-likelihood – функция логарифмического правдоподобия.
Akaike information criterion (AIC) – информационный критерий Акаике.
Schwarz Bayesian criterion (BIC) – Критерий Байеса-Шварца.
Hannan-Quinn criterion (HQC) – Критерий Ханана-Квина.
Для проверки адекватности модели в окне model1 (см. рисунок 3.2) нужно выполнить команду: Analysis – Anova
Результаты анализа адекватности модели представлены на рисунке 3.3.
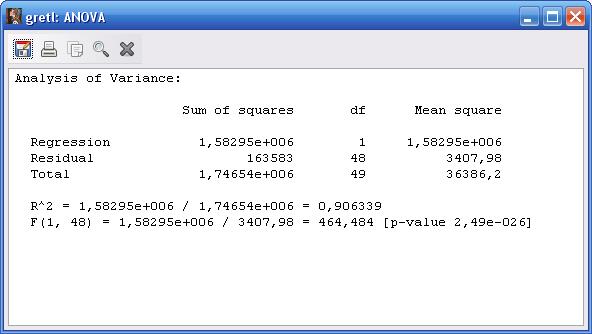
Рисунок 3.3 – Результаты анализа адекватности регрессионного уравнения
Для получения графика фактических данных и расчетных в окне model1 (см. рисунок 3.2.) нужно выполнить команду: Graphs -fitted actual plot- against x1.
Рисунок 3.3 – Графическое представление результатов регрессионного анализа
4 ПРИМЕР РЕГРЕССИОННОГО АНАЛИЗА
Необходимо оценить эффективность рекламы.
Имеются данные о числе показов рекламы в месяц и натуральном объеме продаж продукции.
Они представлены в таблице 4.1.
Таблица 4.1 – Данные для анализа
| Продажа (тыс.штук), Y | Реклама (число показов в месяц), X |
Ход решения задачи
1. Предположим, что объем реализации товаров зависит от числа показов рекламы. Для проверки этого предположения построим график и рассчитаем коэффициент корреляции.
Рисунок 4.1 – Меню построения графика
Рисунок 4.2 – График зависимости продаж от числа показа рекламы
Рисунок 4.3 – Диалоговое окно для расчета коэффициента корреляции
Рисунок 4.4 – Результат расчета коэффициента корреляции между данными
График показывает, что объем продаж возрастает с увеличением числа телевизионных роликов, демонстрируемых ежемесячно. Коэффициент корреляции между данными составляет 0,88, что свидетельствует о сильной положительной связи между переменными.
2. Построим регрессионные модели вида:
и 
,
где 
– число показов в месяц,
– продажа изделий (тыс. шт.).
Использование команды Model - ordinary least squares даст нам следующий результат:
|
|
|
