 |
Model 1: OLS estimates using the 20 observations 2005:01-2006:08
|
|
|
|
Dependent variable: Q
Coefficient std. error t-ratio p-value
---------------------------------------------------------
reklama 36,6019 1,46053 25,06 5,09E-016 ***
Mean of dependent variable = 398,15
Standard deviation of dep. var. = 112,733
Sum of squared residuals = 100189
Standard error of the regression = 72,6163
Unadjusted R-squared = 0,97064
Adjusted R-squared = 0,97064
Centered R-squared = 0,58508
F-statistic (1, 19) = 628,042 (p-value < 0,00001)
Durbin-Watson statistic = 1,61167
First-order autocorrelation coeff. = 0,13405
Log-likelihood = -113,57
Akaike information criterion (AIC) = 229,139
Schwarz Bayesian criterion (BIC) = 230,135
Hannan-Quinn criterion (HQC) = 229,334
Рисунок 4.5 - Результаты регрессионного анализа
Регрессионное уравнение будет иметь вид:
,
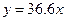где х – число показов рекламы в месяц,
у – объем реализации продукции.
Coefficient std. error t-ratio p-value
---------------------------------------------------------
reklama 36,6019 1,46053 25,06 5,09E-016 ***
При уровне значимости 5% принимается гипотеза о значимости коэффициентов регрессионного уравнения (P<0.05).
Standard error of the regression = 72,6163
Стандартная ошибка регрессии – 72,6163, что является достаточно высоким результатом по сравнению со средним значением зависимой переменной – 398,15.
Unadjusted R-squared = 0,97064
Adjusted R-squared = 0,97064
Коэффициент детерминации 97% ‑ это та часть общей вариации зависимой переменной, которая объясняется уравнением регрессии. Значение коэффициента детерминации свидетельствует о высокой степени соответствия построенной модели исходным данным.
F-statistic (1, 19) = 628,042 (p-value < 0,00001)
На основе результатов дисперсионного анализа при уровне значимости в 5% можно принять альтернативную гипотезу, то есть можно утверждать, что уравнение регрессии адекватно отражает зависимость между переменными.
Проведем оценку регрессионного уравнения вида 
Результаты представлены ниже.
Model 2: OLS estimates using the 20 observations 2005:01-2006:08 Dependent variable: Q
Coefficient std. error t-ratio p-value
|
|
|
--------------------------------------------------------
const 140,009 33,7467 4,149 0,0006 ***
reklama 24,8212 3,03544 8,177 1,79E-07 ***
Mean of dependent variable = 398,15
Standard deviation of dep. var. = 112,733
Sum of squared residuals = 51214,7
Standard error of the regression = 53,341
Unadjusted R-squared = 0,78790
Adjusted R-squared = 0,77612
Degrees of freedom = 18
Durbin-Watson statistic = 2,12506
First-order autocorrelation coeff. = -0,115888
Log-likelihood = -106,859
Akaike information criterion (AIC) = 217,719
Schwarz Bayesian criterion (BIC) = 219,71
Hannan-Quinn criterion (HQC) = 218,107
Как видно из полученных результатов регрессионное уравнение имеет вид:
Standard error of the regression = 53,341
Средняя ошибка регрессии ниже, чем в предыдущем случае и составляет 53,341.
При уровне значимости 5% принимается гипотеза о значимости коэффициентов регрессионного уравнения (P<0.05).
Unadjusted R-squared = 0,78790
Adjusted R-squared = 0,77612
Коэффициент детерминации 78.8% ‑ Значение коэффициента детерминации свидетельствует о более низкой степени соответствия построенной модели исходным данным в отличие от предыдущей.
Analysis of Variance:
Sum of squares df Mean square
Regression 190250 1 190250
Residual 51214,7 18 2845,26
Total 241465 19 13414,7
R^2 = 190250 / 241465 = 0,787900
F(1, 18) = 190250 / 2845,26 = 66,8655 [p-value 1,79e-007]
На основе результатов дисперсионного анализа при уровне значимости в 5% можно принять альтернативную гипотезу, то есть можно утверждать, что уравнение регрессии адекватно отражает зависимость между переменными.
Для выбора модели составим таблицу статистических оценок уравнения регрессии и сравним критерии качества регрессионного уравнения в первом и втором случае.
Таблица 4.2 – Статистические оценки регрессионных моделей
|
| |
| Значимость коэффициентов по критерию Стъюдента | значим | значимы |
| Адекватность регрессионного уравнения по критерию Фишера | адекватно | адекватно |
| Стандартная ошибка регрессии | 72,6163 | 53,341 |
| Коэффициент детерминации | 0,97064 | 0,78790 |
| Log-likelihood | -113,57 | -106,859 |
| AIC | 229,139 | 217,719 |
| BIC | 230,135 | 219,71 |
| HQC | 229,334 | 218,107 |
Анализируя характеристики двух моделей, можно прийти к выводу о том, что в первой модели коэффициент детерминации выше, а во второй модели меньше ошибка и лучше показатели качества регрессионного уравнения. Следовательно, более точной является вторая модель.
|
|
|
Таким образом, модель зависимости объема продаж от числа показов рекламы в месяц будет иметь вид:
В случае, если показы рекламных роликов не будут осуществляться, то объемы продаж будут находиться на отметке 140 единиц. Уравнение регрессии показывает, что если число показов в месяц возрастет на единицу, то это приведет к увеличению объемов продаж на 24.8 единиц.
5 ЗАДАНИЕ ПО ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ
Задание 1
Компания «Лагуна», которая обеспечивает стеклянными бутылками множество изготовителей безалкогольных напитков, обладает следующей информацией, относящейся к числу ящиков при одной отгрузке и соответствующим транспортным затратам (см. Таблицу 5.1).
Таблица 5.1 ‑ Данные к заданию 1
| Число ящиков на отгрузку | Транспортные затраты (грн) | ||||
| Вариант | |||||
Проведите анализ затрат в зависимости от числа ящиков к разгрузке. Представьте экономическое обоснование результатов регрессионного анализа. Спрогнозируйте сумму затрат при росте отгрузки до 1000 ящиков.
Задание 2
Компания «Фаворит» продает компьютерные программы. Ее отдел маркетинга получил данные (количество программ, цены программ, средний доход потребителей, приобретающих такой товар) из филиалов компании, расположенных по территории области (см. Таблицу 5.2).
Проведите анализ спроса на продукцию фирмы. Подберите наилучшую модель, описывающую зависимость спроса от цены или дохода (линейную, квадратичную, кубическую). Представьте экономическое обоснование результатов регрессионного анализа.
Таблица 5.2 – Данные для анализа к заданию 2
| Количество | Цена, грн | Доход, грн | ||||||
| Вариант | Вариант | |||||||
|
|
|
Задание 3
Менеджер торгового предприятия, занимающегося реализацией продуктов питания, имеет следующие данные о ежеквартальной оборачиваемости оборотных средств и уровне рентабельности. Проанализируйте эти данные и составьте регрессионную модель зависимости рентабельности от оборачиваемости оборотных средств.
Таблица 5.3 – Исходные данные к выполнению задания 3.
| квартал | ||||||||
| Вариант 1 | ||||||||
| Число оборотов | 5,49 | 4,68 | 4,67 | 4,54 | 4,56 | 6,02 | 5,72 | 5,43 |
| Уровень рентабельности, % | 0,78 | 0,38 | 0,21 | 0,51 | 0,95 | 1,05 | 0,83 | 0,98 |
| Вариант 2 | ||||||||
| Число оборотов | 7,8 | 4,3 | 5,2 | 6,3 | 7,1 | 7,6 | 7,8 | 8,2 |
| Уровень рентабельности, % | 6,5 | 0,5 | 1,2 | 1,5 | 2,8 | 3,2 | 3,5 | 4,3 |
| Вариант 3 | ||||||||
| Число оборотов | 10,4 | 10,6 | 11,2 | 10,1 | 9,8 | 9,7 | 10,2 | |
| Уровень рентабельности, % | 3,2 | 5,3 | 3,9 | 0,95 | 1,05 | 0,83 | 0,98 | |
| Вариант 4 | ||||||||
| Число оборотов | 4,3 | 4,6 | 4,7 | 4,8 | 4,45 | 4,2 | 4,9 | |
| Уровень рентабельности, % | 9,8 | 11,2 | 12,5 | 13,6 | 10,6 | 9,1 | 14,6 | 15,7 |
| Вариант 5 | ||||||||
| Число оборотов | 7,8 | 7,2 | 6,5 | 6,2 | 6,1 | 5,8 | 5,9 | 5,6 |
| Уровень рентабельности, % | 10,1 | 9,8 | 8,8 | 8,1 | 7,2 | 6,5 | 6,2 | 5,1 |
| Вариант 6 | ||||||||
| Число оборотов | 10,4 | 10,6 | 11,2 | 10,1 | 9,8 | 9,7 | 10,2 | |
| Уровень рентабельности, % | 5,6 | 5,8 | 6,5 | 8,1 | 7,1 | 6,9 | 7,2 |
|
|
|
Задание 4
По статистическим данным, описывающим зависимость уровня рентабельности на предприятии от удельного веса продовольственных товаров в товарообороте построить уравнение регрессии.
Таблица 5.4 – Исходные данные к заданию 4
| квартал | ||||||||
| Вариант 1 | ||||||||
| Удельный вес продовольственных товаров в товарообороте, %. | ||||||||
| Уровень рентабельности, % | ||||||||
| Вариант 2 | ||||||||
| Удельный вес продовольственных товаров в товарообороте, %. | 11,5 | 9,9 | 9,5 | 8,3 | 11,2 | |||
| Уровень рентабельности, % | 8,1 | 9,2 | 10,3 | 11,1 | 12,4 | 13,2 | 10,9 | 8,9 |
| Вариант 3 | ||||||||
| Удельный вес продовольственных товаров в товарообороте, %. | 5,6 | 6,5 | 7,1 | 8,2 | 8,3 | 8,6 | 9,1 | |
| Уровень рентабельности, % | 1,2 | 2,4 | 3,6 | 4,8 | 6,8 | 7,7 | 8,2 | 10,1 |
| Вариант 4 | ||||||||
| Удельный вес продовольственных товаров в товарообороте, %. | 22,4 | 25,6 | 28,5 | 32,4 | 36,9 | 34,6 | 38,7 | 40,1 |
| Уровень рентабельности, % | 15,4 | 16,2 | 17,1 | 18,9 | 19,1 | 20,1 | 21,4 | 23,6 |
| Вариант 5 | ||||||||
| Удельный вес продовольственных товаров в товарообороте, %. | 95,6 | 90,1 | 85,4 | 78,3 | 75,6 | 65,3 | 60,4 | 32,4 |
| Уровень рентабельности, % | 5,6 | 6,1 | 6,3 | 7,1 | 8,2 | 9,4 | 9,6 | 12,3 |
| Вариант 6 | ||||||||
| Удельный вес продовольственных товаров в товарообороте, %. | 35,6 | 34,5 | 36,8 | 39,5 | 37,3 | 34,6 | 39,5 | 38,6 |
| Уровень рентабельности, % | 5,4 | 5,6 | 5,8 | 5,9 | 5,2 | 5,1 | 4,9 | 5,2 |
6 ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Изучить методические указания к выполнению работы.
2. Подготовить заготовку отчета по лабораторной работе: в соответствии с заданием сформулировать цель исследования.
3. Выполнить задания 1-4 в соответствии с вариантом: исследовать характер зависимости, построить регрессионные модели, выбрать и проанализировать наиболее точную регрессионную модель.
4. По результатам выполнения заданий подготовить отчет с выводами, результатами расчетов и графиками.
5. Ответить на контрольные вопросы.
6. Защитить лабораторную работу.
7. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Дайте определение регрессионного анализа.
2. Для каких целей используется метод наименьших квадратов в регрессионном анализе. Поясните суть метода наименьших квадратов.
3. Дать определение адекватности. Какие гипотезы необходимо проверить при анализе адекватности модели.
4. Какова цель использования дисперсионного анализа при регрессионном анализе.
|
|
|
5. Какие виды гипотез используются в регрессионном анализе и почему.
6. Пусть модель задана в виде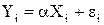 
. Выведите формулы оценивания коэффициента 
, 
, 
и 
.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Болч Б., Хуань К. Дж. Многомерные статистические методы для экономики/ Пер. с англ. А.Д. Плитмана; Под ред. и с предисл. С.А. Айвазяна. ‑ М.: Статистика, 1979. ‑ 317с.
2. Тюрин Ю.Н., Макаров А.А. Статистический анализ данных на компьютере/ Под ред. В.Э. Фигурнова. ‑ М.: ИНФРА-М, 1998 ‑ 528с.
3. Управленческая экономика и стратегия бизнеса: Учеб. пособие для вузов/ Пер. с англ. под ред. А.М. Никитина. – М.: ЮНИТИ-ДАНА, 1999. – 743с.
|
|
|
