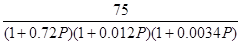Исследование системы на устойчивость по критерию Найквиста.

ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ

 

Исследовать систему автоматического управления, структурная схема которого представлена на рисунке [1].

 

u(t)                                                                                                          y(t)

 

 

№ варианта	Регулятор	Параметры звеньев системы					ω	A0
		K0	T1	T2	T3	T4
19		75	0.23	0.72	0.012	-	1.7	15

 

ВВЕДЕНИЕ

 

 Теория автоматического управления – это совокупность целесообразных действий, направленных на достижение заранее поставленных целей.

Объект управления – это техническое устройство, в котором протекает управляемый процесс.

В данной курсовой работе цели исследование – это изучение основных понятий ознакомится с классификацией систем автоматического регулирования.

Изучить основные понятия и определения устойчивости автоматических систем; алгебраические критерии устойчивости Гурвица; Михайлова, частотныеpкритерии устойчивости Найквиста и их различные формулировки; понятиеyобласти устойчивости в пространстве параметров, получить понятие о корнях характеристического уравнения.

Изучить и сформировать представление о математической модели системы, о переходных процессах CAУ, о передаточной функции CАУ.

УСТОЙЧИВОСТЬ СИСТЕМЫ.

 

ИССЛЕДОВАТЬ УСТОЙЧИВОСТЬ СИСТЕМЫ

Исследование устойчивости замкнутой системы по корням характеристического уравнения системы.

 

Для того чтоб исследовать систему на устойчивость по корням характеристического уравнения необходимо записать передаточную функцию системы:

 

Получим характеристическое уравнение замкнутой системы – знаменатель ЗС приравнивается к нулю:

 

Система имеет 4 корня:

P₁ =-31.952, 148.622; P₂ =-148.622, 31.952; P₃ =-21.42; P₄=-5.158

 

Уравнение имеет четыре корня, и они - корни отрицательные или «левые», отсюда следует, что замкнутая система устойчива.

 

Исследование устойчивости замкнутой системы по критерию Гурвица.

 

Система замкнутая, значит, запишем передаточную функцию замкнутой системы с последовательным соединением всех звеньев.

Достаточное условие по критерию Гурвица:

Для того чтобы все корни характеристического уравнения замкнутой системы имели отрицательные вещественные части, достаточно, чтобы при a₀>0 все n-определителей Гурвица были больше нуля. Порядок n = 4, значит, главный определитель Гурвица будет четвертого порядка. Определим коэффициенты Гурвица в уравнении при неизвестных.

а₀ = 0,000029, а₁ = 0,0026, а₂ = 0.732, а₃ = 17.25, a₄=75

Запишем матрицу Гурвица.

=0.0013

 

Вывод: все определители Гурвица больше нуля, следовательно, заданная система является устойчивой.

 

Исследование системы на устойчивость по критерию Михайловa.

 

Для исследования системы на устойчивость по критерию Михайлова необходимо построить годограф Михайлова.

Запишем характеристическое уравнение замкнутой системы.

Подставляем в формулу:

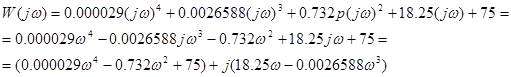
Полученноеpвыражение необходимоpразбить на действительную и мнимуюpчасти:

Re =  - это действительная часть.

Im =  - это мнимая часть.

 

Записываем в сводную таблицу значения для построения Годографа Михайлова:

	Re	Im
0	75	0
10,143	0	182,335
157,529		-7,519*103
5.361*10^-4	75	0
∞	∞	-∞

Рисунок 1- Годограф Михайлова.

Годограф Михайлова начинается на внешней положительной полуоси и при увеличении частоты от 0 до бесконечности последовательном в положительном направлении, (n=4 - порядок) проходит через 4 квадрата.

Исследование системы на устойчивость по критерию Найквиста.

 

Для определения устойчивости по критерию Найквиста, необходимо записать характеристическоеgуравнениеgразомкнутой системы.

Этот критерий позволяет судить об устойчивости замкнутой системы по АФЧХ разомкнутой цепи.

Определить устойчивость разомкнутой системы.

Находим: записываем передаточную функцию разомкнутой системы,

Характеристическое уравнение разомкнутой системы представляет собой знаменатель передаточной функции разомкнутой системы приравненный к нулю.

Запишем его:

Произведение равно нулю тогда, когда один из множителей равен нулю.

P=0 или

(1+0,72p) = 0 или

(1+0,012p) = 0 или

(1+0,0034p) = 0 или

Тогда уравнение имеет четыре корня.

P₁=0; P₂=-1.38; P₃=-83.33; P₄=-294.11

 

Разомкнутая система находится на границе устойчивости, так как имеется один корень, значение которого равно нулю.

Для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении  от 0 до , дополненной на разрыве дугой бесконечного радиуса, не охватывала особую точку с координатами (-1;j0).

Передаточная функция разомкнутой цепи.

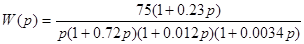
Сделаем замену: , получим:

Рисунок 2 - Годограф Найквиста.

Годограф Найквиста, дополненный дугой бесконечно большого радиуса, не охватывает особую точку (-1; j0). Значит, замкнутая система устойчивая.

 

12	Поделиться:

Воспользуйтесь поиском по сайту: