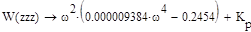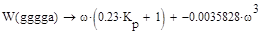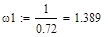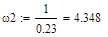Построение области устойчивости системы в области параметрoв T1 и Kp

 

Посторенние области устойчивости с использованием критерия Гурвица затруднено т.к. это система 4 порядка, поэтому применяем критерий Михайлова. Запишем передаточную функцию замкнутой системы где Т₁ и К_р оставим в буквенной форме.

 

 

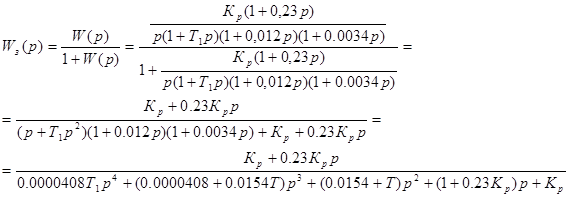
Запишем характеристическое уравнение замкнутой системы (это знаменатель приведенной передаточной функции замкнутой системы):

Заменим p на jω, получим:

Запишем уравнения определяющие границу устойчивости:

 

Решаем их совместно относительно параметров T₁ и K_p

 

 

 

 

 

Построение ЛЧХ системы, определение запаса устойчивости

 

   

Находим частоты сопряжения всех динамических звеньев

 

 

Находим точку 20lg75=37.501

 

 

ОЦЕНКА ПРЯМЫХ ПОКАЗАТЕЛЕЙ КАЧЕСТВА

2.1. Определение прямых показателей качества по переходной характеристике (время регулирования t_p и перерегулирование )

 

Характеристики переходного процесса определяются параметрами системы, видом задающего и возмущающего воздействий начальными условиями. Истинные значения прямых показателей качества получают по переходной характеристике. Получим график переходной характеристике при помощи программы VisSim.

Рисунок 3- График переходной характеристике.

Рисунок 4 -Т max

Рисунок 5-  График пересечения.

Время регулирования – это промежуток времени по истечению, которого отклонения регулируемой величины от установившегося значения становится меньше некоторой заранее заданной величины, то есть время регулирования характеризует время затухания переходного процесса t_p=0,217 секунд.

Перерегулирование  - это выраженное в процентах отношение максимального отклонения управляемой величины от установившегося значения к  установившемуся значению  =>      (значение не должно превышать 30%).

 

Оценка прямых показателей качества системы

 

Оценка прямых показателей качества по расположению нулей и полюсов замкнутой системы.

 

Характеристическое уравнение замкнутой системы.

Уравнение имеет четыре корня, и они равны:

P₁ =-31.952, 148.622; P₂ =-148.622, 31.952; P₃ =-21.42; P₄=-5.158

Рисунок 6 - Оценка прямых показателей качества.

  Из расположения корней видно то что перерегулирования и время регулирования имеют большие значения, все корни расположены на отрицательной части вещественной оси следовательно система апериодически устойчива.

 

Оценка прямых показателей качества системы по ВЧХ.

 

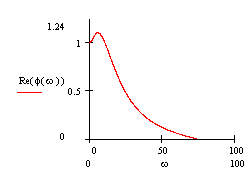
Рисунок  7- Оценка прямых показателей качества системы по ВЧХ.

Определение показателя колебательности системы (по АЧХ замкнутой системы и АФЧХ разомкнутой системы).

Рисунок 8 - АЧХ.

Рисунок 9 - АФЧХ разомкнутой системы

Определение ошибки системы.

 

Определить ошибку системы в установившемся режиме. Получение расчетного и экспериментального графика ошибки системы при отработки входного сигнала с постоянной скоростью.

 

 

 

E=C0 *(ax + b)= 15x+1.7

 

 

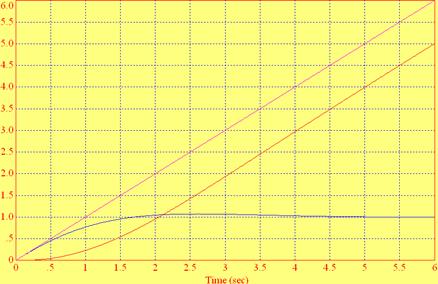
Рисунок 10 – расчетно эксперементальный график ошибки системы

Расчет и посторенние графика реакции системы при подаче на вход гармонического входного сигнала с заданной амплитудой и частотой

A₀=15; ω=1.7

 

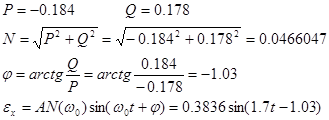
Рисунок 11 – График реакции системы.

Заключение

В результатеgвыполненной работыgследует сделать вывод о том, что система имеет хороший запас устойчивости. Исследуя систему по корням характеристического уравнения, можноgсказать что, разомкнутая система находится на границе устойчивости, так как имеется oдин нулевой корень. Полученные показатели качества позволяют сделать заключение o тoм, что система плавноgи последовательно возвращается в установившееся значение. Из графика видно, что переходный процесс колебательный.

По критериям Гурвица, Михайлова и Найквиста система является устойчивой.

Система работоспособна, с довольно значительной колебательностью и малой полосойgпропускания.

Список использованной литературы

1. Бесекерский В. А., Попов Е. П. Теория система автоматического регулирования. – М.: Наука, 1975.

2. Макаров И.М., Менский Б.М. Линейные автоматические системы    (элементы теории, методы расчета и справочный материал). - 2-е изд., перераб. и доп. - М.: Машиностроение, 1982.

3. Cборник задач по теoрии автоматического регулирования и управления / Под ред. В.А. Бесекерского. - М.: Наука, 1978.

4. Теория автоматическогоoуправления.: Учебник. В 2-х частях/ Под ред. А. А. Воронова. – М.: Высшая школа, 1986.

 

12	Поделиться:

Воспользуйтесь поиском по сайту: