 |
Учебно-методическое обеспечение самостоятельной работы студентов. Оценочные средства для текущего контроля успеваемости, промежуточной аттестации по итогам освоения дисциплины.
|
|
|
|
С целью контроля знаний предусмотрены самостоятельные работы по основным разделам курса. Промежуточная аттестация состоит в контроле посещаемости, промежуточном тестировании и выполнения текущих домашних заданий. Приведены контрольные вопросы и тест для проведения итоговой аттестации.
Контрольные вопросы.
1. Постановка задачи исследования операций.
2. Примеры модулей исследования операций.
3. Критерий эффективности в детерминированных и вероятностных задачах.
4. Векторный критерий эффективности и способы его преобразования в скалярный.
5. Определение и примеры антагонистических игр.
6. Понятие седловой точки и условия ее существования в антагонистической игре.
7. Матричные игры. Основная теорема теории матричных игр.
8. Основные методы решения матричных игр.
9. Байесовский подход к решению статистических игр.
10. Минимаксный подход к решению статистических игр.
11. Статистические игры с экспериментом, их особенности.
12. Биматричные игры. Теорема о существовании ситуации равновесия в биматричной игре.
13. Примеры экономических и политических ситуаций, моделируемых с помощью биматричных игр.
14. Иерархические системы. Наибольший гарантированный результат Центра.
15. Методы управления иерархическими системами.
16. Задачи о потоках в сетях, их особенности.
17. Методы нахождения максимальных потоков.
18. Основные понятия теории массового обслуживания.
19. Методы исследования марковских систем массового обслуживания.
20. Основные законы распределения в теории надежности.
21. Статистическое моделирование случайных величин.
22. Основные принципы и этапы имитационного моделирования.
Тест для итоговой аттестации
|
|
|
1. Антагонистическая игра может быть задана:
а) множеством стратегий первого и второго игрока.
б) множеством стратегий обоих игроков и функцией выигрыша второго игрока.
2. Цена игры всегда равна верхней цене игры, если обе цены существуют:
а) да.
б) нет.
в) вопрос некорректен.
3. Максимум по x минимума по y и минимум по y максимума по x функции выигрыша первого игрока:
а) всегда равны друг другу.
б) всегда отличаются друг от друга.
в) могут быть и равны, и не равны.
4. Может ли в какой-то антагонистической игре сумма значений функции выигрыша обоих игроков положительна?
а) да.
б) нет.
в) ответ неоднозначен.
5. Пусть в антагонистической игре X =(1;2)- множество стратегий 1-го игрока, Y =(5;8)- множество стратегий 2-го игрока. Является ли пара (1;9) седловой точкой в этой игре:
а) всегда.
б) иногда.
в) никогда.
6. Если известно, что функция выигрыша 1-го игрока всегда больше 1, то значения этой функции в седловой точке могут принимать значения:
а) любые.
б) только положительные.
в) только не более числа 1.
7. Если в антагонистической игре на отрезке [0;1]*[0;1] функция выигрыша 1-го игрока F(x,y) равна C (x-y)2, то при отрицательном значении числа C:
а) седловых точек нет никогда.
б) седловые точки есть всегда.
в) седловые точки могут существовать, и не существовать.
8. Антагонистическая игра может быть задана:
а) множеством стратегий игроков и ценой игры.
б) множеством стратегий обоих игроков и функцией выигрыша первого игрока.
в) обязательно каким-то иным способом.
9. Верхняя цена игры больше верхней цены игры, если оба показателя существуют.
а) да.
б) не всегда.
в) никогда.
10. Смешанная стратегия - это:
а) число.
б) вектор.
в) матрица.
11.Пусть в антагонистической игре X=(1;2)- множество стратегий 1-го игрока, Y=(2;8)- множество стратегий 2-го игрока. Является ли пара (1;2) седловой точкой в этой игре:
а) всегда.
б) иногда.
в) никогда.
|
|
|
12. Седловая точка – это:
1) стратегия одного из игроков.
2) упорядоченная пара, в которой первая составляющая - стратегия первого игрока, вторая - стратегия второго игрока.
3) что-то иное.
13. Функция выигрыша первого игрока зависит:
а) от одной переменной.
б) от двух переменных.
в) от трех переменных.
14. Матричная игра – это частный случай антагонистической игры, при котором обязательно выполняется одно из требований:
а) один из игроков имеет бесконечное число стратегий.
б) оба игрока имеют бесконечно много стратегий.
в) сумма функций выигрыша игроков постоянна.
15. Пусть матричная игра задана матрицей, в которой все элементы одинаковы.
Цена игры существвует:
а) да.
б) нет.
в) нет однозначного ответа.
16. Оптимальная смешанная стратегия для матричной игры состоит из положительных чисел.
а) да.
б) нет.
в) нет однозначного ответа.
17. Цена игры существует для матричных игр в чистых стратегиях всегда.
а) да.
б) нет.
18. Чистая стратегия является частным случаем смешанной:
а) да.
б) нет.
в) не всегда.
19. Если в матрице все столбцы одинаковы и имеют вид (4 3 2 1), то какая стратегия оптимальна для 2-го игрока?
а) первая.
б) вторая.
в) любая из четырех.
20. Какое максимальное число седловых точек может быть в игре размерности 2*3 (матрица может содержать любые числа)
а) 2.
б) 3.
в) 5.
г) иное число.
21. В матричной игре размерности 2*2 имеется 5 седловых точек:
а) всегда.
б) иногда.
в) никогда.
22. Пусть в матричной игре одна из смешанных стратегий 1-го игрока имеет вид (0.5, 0.5), а одна из смешанных стратегий 2-го игрока имеет вид (0.5, 0.3, 0.1,0.1). Какова размерность этой матрицы?
а) 2*4.
б) 4*2.
в) другая размерность.
23. Принцип доминирования позволяет удалять из матрицы за один шаг:
а) целиком столбцы.
б) отдельные числа.
в) подматрицы меньших размеров.
24. В графическом методе решения игр 2*m непосредственно из графика можно найти:
а) оптимальную стратегию 1-го игрока.
б) оптимальную стратегию 2-го игрока.
в) и то, и другое.
25. График нижней огибающей для графического метода решения игр 2*m может быть:
а) гиперболой.
б) прямой.
в) параболой.
26. Чем можно задать матричную игру:
а) одной матрицей.
б) седловой точкой.
в) ценой игры.
27. Биматричная игра может быть определена:
|
|
|
а) двумя матрицами одинаковой размерности.
б) двумя произвольными матрицами.
в) одной матрицей.
28. В биматричной игре размерности 2*4 ситуаций равновесия бывает:
а) не более 2.
б) не более 6.
в) не более 8.
г) нет однозначного ответа.
29. Если в матрицах A и В в биматричной игре все элементы одинаковы, то ситуации равновесия есть:
а) всегда.
б) иногда.
в) никогда.
30. Седловая точка – это частный случай ситуации равновесия:
а) да.
б) нет.
в) вопрос некорректен
31. В биматричной игре элемент bij представляет собой:
а) выигрыш 2-го игрока при использовании им i-й стратегии, а 2-м – j-й стратегии.
б) оптимальную стратегию 1-го игрока при использовании противником i-й или j-й стратегии.
в) выигрыш 2-го игрока при использовании им j-й стратегии, а 1-м – i-й стратегии.
32. В биматричной игре элемент aij соответствует ситуации равновесия. Возможны следующие ситуации:
а) этот элемент строго больше всех в столбце.
б) этот элемент меньше всех в столбце.
в) в столбце есть элементы и больше, и меньше, чем этот элемент.
33. Биматричная игра может быть определена:
а) стратегиями игроков.
б) стратегиями игроков и функцией выигрыша 1-го игрока.
в) чем-то иным.
34. В биматричной игре размерности 2*N может быть ситуаций равновесия:
а) не более 2+N.
б) не более N.
в) не более 2*N.
35. Бывает ли в биматричной игре размерности 3*3 ровно 7 ситуации равновесия?
а) всегда.
б) иногда.
в) никогда.
36. Матричная игра – это частный случай биматричной, при котором всегда справедливо:
а) матрица А равна матрице В, взятой с обратным знаком.
б) матрица A не совпадает с матрицей В.
в) Произведение матриц А и В -единичная матрица..
37. В биматричной игре элемент bij представляет собой:
а) выигрыш 2-го игрока при использовании им j-й стратегии, а 1-м – i-й стратегии,
б) оптимальную стратегию 2-го игрока при использовании противником i-й или j-й стратегии/
в) что-то иное.
38. В биматричной игре элемент bij соответствует ситуации равновесия. Возможны следующие ситуации:
а) в столбце есть элементы, равные этому элементу.
б) этот элемент меньше некоторых в строке.
|
|
|
в) этот элемент меньше всех в строке.
Задачи для самостоятельного решения.
1. Дана задача принятия решения. В таблице - прибыль города при различных вариантах проведения праздника (тыс. руб.).
| Погода | Праздник на открытом воздухе | Праздник в театре |
| Солнечно (60 %) | ||
| Дождь (40 %) |
Установить, где следует проводить праздник по критериям Лапласа, Вальда и математического ожидания? Каким будет 
в критерии Гурвица, если предпочтение отдано театру?
Ответ: в театре, в театре, на открытом воздухе, 
.
2. Найти в антагонистической игре седловую точку, если она есть.
.
Ответ: седловой точки нет.
Ответ: (0,1).
3. Матрица А в матричной игре имеет вид 
.
Установить, при каких x и y в матрице есть седловые точки.
Ответ: при 
4. Матрица А в матричной игре имеет вид 
.
Установить, при каких x в матрице есть седловые точки.
Ответ: при любых значениях х седловых точек нет.
5. Задача о зимней эксплуатации лесовозной дороги.
Предположим, что при заготовке леса зимой есть выбор - делать или не делать предварительную расчистку дороги. При этом известны предполагаемые высоты снежного покрова и матрица доходов при применении той или иной стратегии. Заготовитель – игрок 1, природа – игрок 2.
| 1 \ 2 | 20 мм | 40 мм | 60 мм | 100 мм |
| Не делать | -1 | |||
| Делать |
Найти цену игры.
Ответ: v= 2.5.
6. Найти с помощью графического метода, предварительно вычеркнув доминируемый столбец или строку, решение матричной игры с
матрицей A = 
.
Ответ: 
7. Найти оптимальные стратегии игроков в игре с
матрицей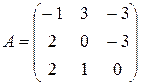 
.
Ответ: 
(1/3,2/3,0); 
(1/5,3/5,1/5).
8. Матрица А в биматричной игре имеет вид 
.
Установить, какой должна быть матрица B, чтобы игра имела чистые ситуации равновесия.
Ответ: должно выполняться хотя бы одно из трех условий:
a) 
максимум в первой строке; б) во второй строке есть элементы, не меньшие, чем 
; в) в третьей строке есть элементы, не меньшие, чем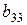 
.
9. Найти смешанные ситуации равновесия в игре с матрицами
A = 
, B = 
.
Ответ: (2/5,3/5); 
(2/3,1/3).
Рекомендации к самостоятельной работе студентов.
| Наименование основных тем или разделов | Самостоятельная работа студентов |
| 1. Предмет и модели исследования операций | /б) 3/, гл.1, п. 2 |
| 2.Многокритериальные задачи | /б) 10/, ч.1, п. 5-6. |
| 3. Антагонистические игры | /б) 1/, гл.2, п. 5 |
| 4. Матричные игры и методы их решения | /а) 2/, п. 5 |
| 5. Теория статистических решений | /б) 1/, гл.3, п. 1-2 |
| 6. Биматричные игры | /б) 10/, ч. 3, п.16 |
| 7. Принятие решений в иерархических системах | /б) 8/,гл. 2, п. 10 |
| 8. Задачи сетевого планирования | /б) 4/, гл. 1, п.3 |
| 9. Основные понятия теории массового обслуживания и теории надежности. | /б) 5/, гл. 1, п. 1.1, 1.2, 1.3. |
| 10. Введение в статистическое моделирование | /б) 7/, гл.1, п.1-2 |
|
|
|
Задания для промежуточной аттестации.
| № варианта | Величины, входящие в расчеты | № варианта | Величины, входящие в расчеты | ||||||
| s | t | u | v | s | t | u | v | ||
I. Подсчитать 
и найти седловые точки (если они есть) для игр со следующими матрицами:
1) 
;
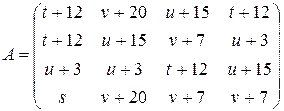2) 
;
3) 
.
Предположим, что элемент 
неизвестен. Как в зависимости от значения этого элемента меняется множество седловых точек?
II. Пусть Г =(X, Y, F) - антагонистическая игра, где X=Y= [- u,v ], 
Найти 
и седловые точки (если они есть).
III. Найти чистые ситуации равновесия в биматричной игре с матрицами
Предположим, что элементы 
неизвестны. Как в зависимости от значений этих элементов меняется множество ситуаций равновесия?
IV. Решить графическим методом матричную игру с матрицей A
.
Выполнить поиск решения той же игры методом Брауна-Робинсон (5 итераций), предположив, что на первом шаге каждый игрок выбирает стратегию 1. На каждом шаге найти 
К основным учебно-методическим средствам обеспечения самостоятельной работы студентов относятся ресурсы научной библиотеки СГУ, электронные методические материалы, указанные в п.7.
|
|
|
