 |
Математическая постановка задачи оптимизации
|
|
|
|
Принятие решений (выбор)
Будем представлять принятие решения как действие над множеством альтернатив, в результате которого получается подмножество выбранных альтернатив (обычно это одна альтернатива, что не обязательно, а иногда и невозможно).
Последствия выбора могут быть точно известны (выбор в условиях определенности ), иметь вероятностный характер, когда известны вероятности возможных исходов после сделанного выбора (выбор в условиях риска ), или иметь неоднозначный исход, не допускающий введения вероятностей (выбор в условиях неопределенности)
Три основных языка описания выбора:
- критериальный язык,
- язык бинарных отношений,
- язык функций выбора.
КРИТЕРИАЛЬНЫЙ ЯЗЫК ОПИСАНИЯ ВЫБОРА
Пусть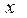 
— некоторая альтернатива из множества X. Считается, что для всех 
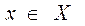может быть задана функция 
, которая называется критерием (критерием качества, целевой функцией, функцией предпочтения, функцией полезности и т.д.) и обладает тем свойством, что если альтернатива 
предпочтительнее альтернативы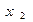 
(будем обозначать это 
), 
и обратно.
Если теперь сделать еще одно важное предположение, что выбор любой альтернативы приводит к однозначно известным последствиям (т.е. считать, что выбор осуществляется в условиях определенности) и заданный критерий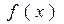 
численно выражает оценку этих последствий, то наилучшей альтернативой 
является, естественно, та, которая обладает наибольшим (или наименьшим) значением критерия:
. 
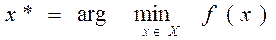(1)
Задачи (1), связанные с нахождением минимума или максимума критерия 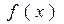, называются экстремальными или оптимизационными задачами.
Оптимизация (выбор) в экономическом анализе
а)Простейшая модель фирмы
|
|
|
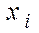– затраты 
- производственного ресурса, 
,в течение некоторого периода времени,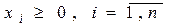 
.
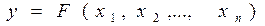– производственная функция, связывающая объем производимого продукта 
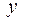с объемами используемых ресурсов;
– цена продукта,
– заданные цены ресурсов.
Предполагается, что ресурсы доступны, а продукт может быть продан в любом количестве.
Рациональное экономическое поведение – выбор объемов ресурсов и выпуска продукции на основе максимизации прибыли
(2)
- выручка от реализации продукции;
- затраты, связанные с производством продукта.
Задача: нахождение таких неотрицательных величин используемых объемов ресурсов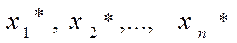 
, при которых
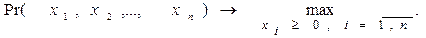(2а)
Математическая постановка задачи оптимизации
Рассмотренные выше задачи принято называть задачами статической оптимизации.
Основными понятиями статической оптимизации являются понятия целевой функции, управляющих переменных, допустимого множества и параметров задачи. Рассмотрим эти понятия.
Целевая функция – это функция, соответствующая критерию качества. ЦФ представляет собой функцию многих переменных, с помощью которой дается математическое изложение цели задачи. Целевая функция обычно представляется в виде
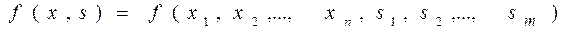, (3)
где 
– переменные задачи.
В задаче оптимизации принято различать два типа переменных – управляющие переменные и параметры задачи. Под управляющими переменными понимаются те переменные модели, изменение которых приводит к достижению цели, т.е. к достижению максимального (минимального) значения целевой функции. Наоборот, параметры задачи не могут быть использованы для увеличения значения целевой функции – они либо заданы, либо являются неопределенными (последнее значительно усложняет решение задачи оптимизации).
В примере управляющими переменными являются величины потребления ресурсов 
, а параметрами задачи являются цены ресурсов и продукта, то есть величины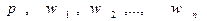 
.
|
|
|
Целевой функцией является прибыль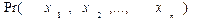 
.
В рамках данного курса будут рассматриваться исключительно так называемые детерминированные задачи оптимизации, то есть задачи с заданными значениями параметров.
.
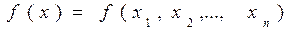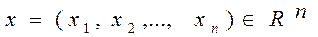
В общем случае, если вектор управляющих переменных х удовлетворяет ограничениям задачи, он называется допустимым, а множество всех допустимых векторов образует допустимое множество решений X. Допустимое множество является подмножеством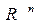 
.
Так как задача заключается в выборе вектора управляющих переменных из допустимого множества, то в любой нетривиальной задаче оно является непустым и содержит, по крайней мере, две различные точки (два решения). В этом случае можно сформулировать задачу минимизации (максимизации).
Задача минимизации состоит в поиске такого вектора управляющих переменных из допустимого множества 
, при котором целевая функция принимает минимальное значение:
или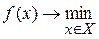 
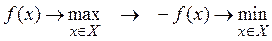
Определение. Точка 
называется точкой локального минимума функции 
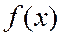на множестве 
, если 
и соответствующая 
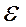-окрестность 
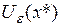точки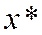 
такие, что f (х*) 
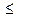f (х) при всех 
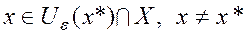(4)
Определение. Точка х*ÎX называется точкой строгого локального минимума функции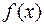 
на множестве 
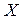, если 
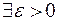и соответствующая 
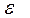-окрестность 
точки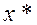 
такие, что f (х*) < f (х) при всех 
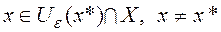. (5)
Глобальный минимум функции 
на множестве 
f (х*) ≤ f (х) при всех х Î X, 
Строгий глобальный минимум функции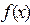 
на множестве 
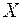f (х*) < f (х) при всех х Î X,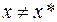 
Решение задачи сводится к поиску конечного числа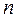 
переменных 
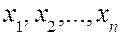на множестве 
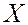, при которых ЦФ достигает минимального (экстремального) значения. Такие задачи называются конечномерными экстремальными или оптимизационными задачами.
Сделаем несколько терминологических замечаний.
Замечание 1. В теории и методах оптимизации часто используется понятие э кстремума. Экстремум – это обобщающее понятие для максимума и минимума, которое означает максимум в задачах максимизации и минимум в задачах минимизации.
Точка экстремума – это точка, в которой целевая функция достигает экстремума. Различают точки глобального экстремума и локального экстремума. Точка глобального экстремума всегда является также и точкой локального экстремума. Обратное неверно.
|
|
|
Экстремальное значение – это значение целевой функции в экстремальной точке.
Замечание 2. Задачу оптимизации с ограничениями на управляющие переменные называют задачей условной оптимизации, а максимум (минимум) в рассматриваемой задаче называют условным.
Замечание 3. Целевая функция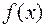 
часто называется критерием оптимизации, поскольку является критерием выбора того или иного вектора хÎX.
Замечание 4. Вектор управляющих переменных часто называют вектором решений или вектором управлений.
Виды экстремумов
1) максимум или минимум;
2) локальный или глобальный;
3) условный или безусловный;
4) строгий или нестрогий;
5) внутренний или граничный (краевой); Внутренний экстремум – это такой максимум или минимум, который достигается во внутренней точке множества 
. Граничный (краевой) экстремум достигается на границе множества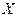 
.
|
|
|
