 |
Задача безусловной оптимизации (задача без ограничений)
|
|
|
|
(6)
Задача условной оптимизации (задача с ограничениями или задача математического программирования)
(7)
Задача безусловной оптимизации
Постановка и схема решения задачи
Данные: 
;
Модель: 
;
- управляющие переменные;
Задача безусловной оптимизации имеет вид:
(6)
Предполагается, что функция 
дважды непрерывно дифференцируема всюду на 
, т.е. в точке 
имеет градиент
и матрицу Гессе
.
Схема решения задачи оптимизации может выглядеть следующим образом:
1. Находятся все точки локальных минимумов;
2. Вычисляются значения функции 
во всех найденных точках и выбирается точка с наименьшим значением функции. Это и есть решение задачи.
Необходимые и достаточные условия наличия локального экстремума
Теорема 1 Необходимое условие наличия локального экстремума
Пусть 
- непрерывно дифференцируемая функция в точке 
. Если 
- точка локального минимума (максимума) функции 
, то
(7)
Точка 
, удовлетворяющая условию (7), называется стационарной точкой функции 
или задачи (1).
Для выявления искомой точки на множестве стационарных используется условие локальной оптимальности второго порядка
Теорема 2
Пусть 
- дважды непрерывно дифференцируемая функция в некоторой окрестности точки 
.Если 
- точка локального минимума функции 
, то матрица Гессе неотрицательно определена, т.е. 
,(8) где 
Теорема 3 Достаточное условие локальной оптимальности
Пусть - дважды непрерывно дифференцируемая функция в некоторой окрестности точки 
. Если 
удовлетворяет условию (2), а матрица Гессе положительно определена, т.е.
, (9)
то 
- точка строгого локального минимума функции 
Знакоопределенность матрицы. Критерий Сильвестра
|
|
|
Для установления знакоопределенности квадратной матрицы 
предлагается следующая схема:
1. Если знаки всех угловых миноров матрицы 
положительны, то она является положительно определенной 
;
2. Если знаки угловых миноров чередуются, начиная с минуса, то матрица 
отрицательно определена 
;
2.4. Одномерная минимизация
Для функции одной переменной 
необходимые условия локальной оптимальности определяется следующими соотношениями:
(1)
Достаточное условие 
Модель спроса на наличные деньги
Согласно этой модели определяются размеры необходимой суммы наличных денег. Предполагается, что годовая потребность (годовой спрос) в наличных деньгах субъекта, которые находятся на банковском счете под процент 
, известна - 
. При необходимости субъект посещает банк и снимает со счета определенную сумму денег - 
, которую он использует для покрытия своих расходов. Его запас наличности становится 
, а затем начинает уменьшаться с интенсивностью 
. Когда денежный запас исчерпан 
, следует новое обращение в банк и т.д. Графически эту процедуру можно представить следующим образом
Средний уровень денег на руках 
- комиссионные расходы, связанные с однократным заказом денег в банке
- число посещений банка в год
Годовые затраты на банковские операции 
Альтернативные потери от хранения денег «на руках» (недополучение банковского процента)
- формула Баумоля – Тобина
2.5. Алгоритмы многомерной оптимизации
(1)
Градиентные методы поиска
Методы используют информацию о градиенте целевой функции и относятся к методам первого порядка.
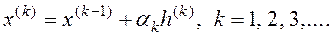(3)
дифференцируема на 
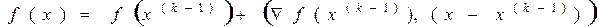(4)
(5)
Поскольку 
, то
(6)
(7)
Из свойства скалярного произведения
(8)
(9)
градиентные методы
,
(10)
Методы спуска
1. Простейший градиентный метод 
;
2. Метод наискорейшего спуска
|
|
|
(11)
Из (11) следует:
3. Градиентный метод с дроблением шага
3.1. 
часто 
;
3.2. 
к следующей итерации
Вычислительная процедура
1. 
,
2. 
,
3. 
,
4. 
5. Проверка условий останова: если выполняются 
;иначе к п. 2
Особенности методов:
- относятся к локальным методам оптимизации;
- используются для решения как одномерных, так и многомерных экстремальных задач;
- выпуклая ЦФ – метод сходится к точке минимума;
сильно выпуклая ЦФ - метод сходится к точке минимума с линейной скоростью;
невыпуклая ЦФ - метод сходится ко множеству стационарных точек
· градиентные методы относятся к методам спуска 
;
низкая скорость сходимости в окрестности точки минимума; метод чувствителен к ошибкам вычислений; градиентные методы целесообразно применять на начальном этапе оптимизационной процедуры.
Метод Ньютона
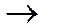
(1)
Процедура поиска
(2)
Из (1) имеем
, (3)
(3) в (2)
(4)- оптимизационный метод Ньютона
Особенности метода Ньютона
1. Трудоемкость, обусловленная вычислением и обращением матрицы Гессе на каждой итерации;
2. Выбор 
;
3. Метод Ньютона сходится к точке минимума произвольной ЦФ с квадратичной скоростью, если матрица Гессе 
положительно определена, а 
располагается «достаточно близко» к 
.
Метод Ньютона с регулировкой шага:
(5)
, 
,
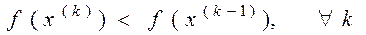Скорость сходимости – сверхлинейная;
квадратичная 
|
|
|
