 |
Решение обратной задачи линейной размерной цепи
|
|
|
|
Расчёт линейной размерной цепи и выбор посадок
Выполнил
студент группы ТСП-06 Мисавирова Э.Ф.
дата 15.05.09
подпись
Проверил
доцент кафедры ОМД Еремин А.В.
Магнитогорск 2009
Задание
Таблица 1 - Исходные данные
| Размер, мм | ||||||||
| А 1 | А 2 | А 3 | А 4 | А 5 | А 6 | А ∆ | D 1 | D 2 |
| 60+0, 19 | 21+0,13 | 10-0,09 | 20-0,13 | 40-0,16 | 10-0,09 | 1+0,35 | 60 | 80 |
Рисунок 1. - Сборочная единица: 1-корпус; 2 - большая шестерня; 3-малая шестерня; 4-втулка; 5-вал; 6-шпонка
На рис.1 представлена сборочная единица (фрагмент коробки передач), включающая разъёмный корпус 1, состоящий из двух половин, в каждую из которых неподвижно установлена втулка 4, выполняющая функции подшипника скольжения. Во втулках установлен вал 5 с возможностью свободного вращения. На валу неподвижно с применением шпонки 6 установлена большая шестерня 2 и с возможностью свободного вращения малая шестерня 3. Режим работы сборочной единицы лёгкий.
Даны номинальные и предельные отклонения (см. таблицу исходных данных) размеров деталей, входящих в размерную цепь: А 1; А 2; А 3; А 4; А 5; А 6; А Δ. Известны также номинальные внутренний D 1 и наружный D 2 диаметры втулок.
Выполнить следующее:
решить обратную задачу линейной размерной цепи;
решить прямую задачу линейной размерной цепи;
выбрать посадки при сопряжении вала со втулками, втулок с корпусом и вала с большой и малой шестернями;
графически построить поля допусков выбранных посадок и дать характеристику посадкам;
вычертить эскизы сборочной единицы и деталей, входящих в её состав.
Реферат
Выполнен расчёт линейной размерной цепи на полную взаимозаменяемость с использованием метода максимума-минимума. Решена обратная (проверочная), а затем прямая (проектировочная) задачи линейной размерной цепи.
|
|
|
На составляющие звенья размерной цепи назначены такие допуски, которые позволяют осуществить сборку сборочной единицы без всякой дополнительной обработки деталей при сохранении служебных функций сборочной единицы.
Выбраны посадки и даны их характеристики. Приведены эскизы сборочной единицы и эскизы рабочих чертежей деталей, входящих в сборочную единицу.
Содержание
Введение
1. Расчет размерной линейной цепи
1.1 Решение обратной задачи линейной размерной цепи
1.2 Решение прямой задачи линейной размерной цепи
2 Выбор посадок
2.1 Графическое построение полей допусков выбранных посадок и их характеристики
3 Эскизы сборочной единицы и деталей, входящих в её состав
Заключение
Библиографический список
Введение
Взаимозаменяемость - свойства независимо изготовленных деталей, узлов и сборочных единиц машин и изделий обеспечивать возможность беспригоночной сборки (замены) сопрягаемых деталей в сборочную единицу, а сборочной единицы в изделие без дополнительной обработки при соблюдении предъявляемых к ним технических требований и сохранении функционирования изделия с заданными эксплуатационными показателями.
Нормативной базой взаимозаменяемости является стандартизация.
Взаимозаменяемость лежит в основе важнейших принципов и форм организации современного производства.
Взаимозаменяемость позволяет организовать серийное и массовое производство изделий, а также выполнять сборку и замену (ремонт) деталей на основе кооперирования их изготовления.
В масштабах хозяйства страны это даёт большой экономический эффект.
Задачей курсовой работы является определение условий выполнения полной взаимозаменяемости сборочной единицы на основе расчёта измерений размерной цепи.
Расчет размерной линейной цепи
|
|
|
Решение обратной задачи линейной размерной цепи
Обратная задача линейной размерной цепи является проверочной, или ее еще называют задачей технолога. Сущность расчета заключается в проверке обеспечения заданной точности замыкающего звена при заданных предельных размерах составляющих звеньев.
Составляем схему размерной цепи в соответствии с конструктивным исполнением сборочной единицы.
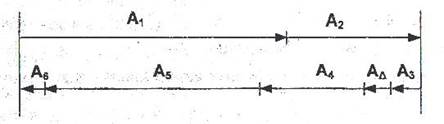
Рисунок 2 -Схема размерной цепи.
Из анализа размерной цепи следует:
А 1, А 2 - увеличивающие размеры;
А3, А4, А5, А6 - уменьшающие размеры;
А ∆ - замыкающее звено размерной цепи (зазор между фланцем втулки и торцом малой шестерни).
Из таблицы исходных данных:
А 1 = 60+0, 19, А 2 = 21+0,13, А3 = 10-0,09, А4 = 20-0,13, А5 = 40-0,16, А6 = 10-0,09, А ∆ = 1+0,35.
Для замыкающего звена заданные величины имеют следующие значения: номинальный размер [ А ∆] = 1,0мм; максимальный предельный размер [ А ∆ макс] = 1,35мм; минимальный предельный размер [ А ∆ мин] = 1,0мм, так как верхнее отклонение замыкающего звена Es (А ∆) = 0,35мм, а нижнее отклонение Ei (А ∆) = 0.
По исходным данным устанавливаем предельные отклонения составляющих звеньев.
Верхнее отклонение увеличивающих размеров:
Es (А 1) = 0, 19мм; Es (А 2) = 0,13мм;
Нижнее отклонение увеличивающих размеров:
Ei (А 1) = 0; Ei (А 2) = 0;
Верхнее отклонение уменьшающих размеров:
Es (А 3) = 0; Es (А 4) = 0;
Es (А 5) = 0; Es (А 6) = 0.
Нижнее отклонение уменьшающих размеров:
Ei (А 3) = - 0,09мм; Ei (А 4) = - 0,13мм;
Ei (А 5) = - 0,16мм; Ei (А 6) = - 0,09мм.
По исходным данным составляющих звеньев вычисляем предельные размеры замыкающего звена А ∆ макс, А ∆ мин.
Определяем номинальный размер замыкающего звена:
А ∆= 
А j - 
А j= (А 1+ А 2) - (А3 + А4+ А5+ А6) = (60+21) - (10+20+40+10) =1мм.
Расчетное значение номинального размера замыкающего звена совпадает с заданным, следовательно, номинальные размеры составляющих звеньев назначены верно и не требуют корректировки.
Определяем верхнее и нижнее отклонения замыкающего звена.
Es (А ∆) = Es (А j) - Ei (А j) = [ Es (А 1) + Es (А 2)] - [ Ei (А 3) + Ei (А 4) + Ei (А 5) + + Ei (А 6)] = (0, 19+0,13) - (-0,09 - 0,13 - 0,16 - 0,09) = 0,79мм.
Ei (А ∆) = Ei (А j) - Es (А j) = [ Ei (А 1) + Ei (А 2)] - [ Es (А 3) + Es (А 4) + Es (А 5) + + Es (А 6)] = 0.
Определяем предельные размеры замыкающего звена:
|
|
|
А ∆ макс = А ∆ + Es (А ∆) =1,0 + 0,79 = 1,79мм.
А ∆ мин = А ∆ + Ei (А ∆) = 1,0 + 0 = 1,0мм.
Проводим сравнение расчетных значений предельных размеров замыкающего звена с заданными значениями по следующим условиям:
А ∆ макс ≤ [ А ∆ макс]; 1,79>1,35;
А ∆ мин ≥ [ А ∆ мин]; 1,0 =1,0.
Первое условие не выполняется, поэтому сборка невозможна с обеспечением полной взаимозаменяемости, и необходимо провести корректировку допусков составляющих размеров, т.е. решить прямую задачу размерной цепи.
|
|
|
12 |
