 |
Структурная алгоритмическая схема системы автоматического управления, обеспечивающей нулевой статизм.
|
|
|
|
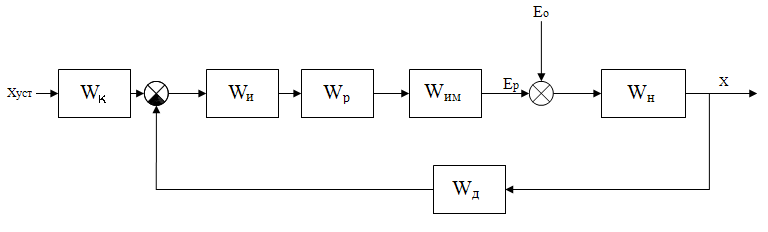
где WР – передаточная функция звена, эквивалентирующего регулятор
WИМ – передаточная функция звена, эквивалентирующего исполнительный механизм
WН – передаточная функция звена, эквивалентирующего нагрузку
WИ – передаточная функция идеального интегрирующего звена
WК – передаточная функция корректирующего звена
WД – передаточная функция звена, эквивалентирующего датчик текущего значения регулируемой переменной
Область устойчивости системы
g w:val="EN-US"/></w:rPr><m:t>РЅ</m:t></m:r></m:sub></m:sSub></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
W``Э – эквивалентная передаточная функция относительно ЭДС ЕО.
Возьмем передаточную функцию относительно ЕО и подставим все передаточные функции, входящие в нее.



После упрощения получаем выражение:

Зная характеристическое уравнение найдем область устойчивости
3 причины нарушения устойчивости:
1) аn=0
2) ao=0
3) Δn-1=0
где ao – коэффициент при высшей степени полинома
аn - свободный член полинома
Δn-1 – предпоследний определитель Гурвица
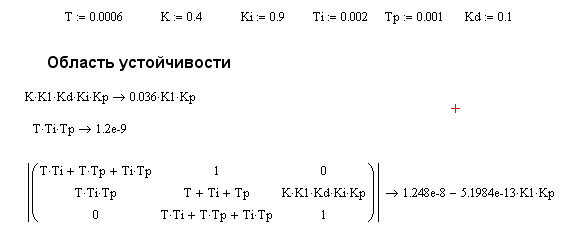
Полученные выражения приравниваем к нулю и таким образом получаем три уравнения связывающие коэффициенты Kр и K1.
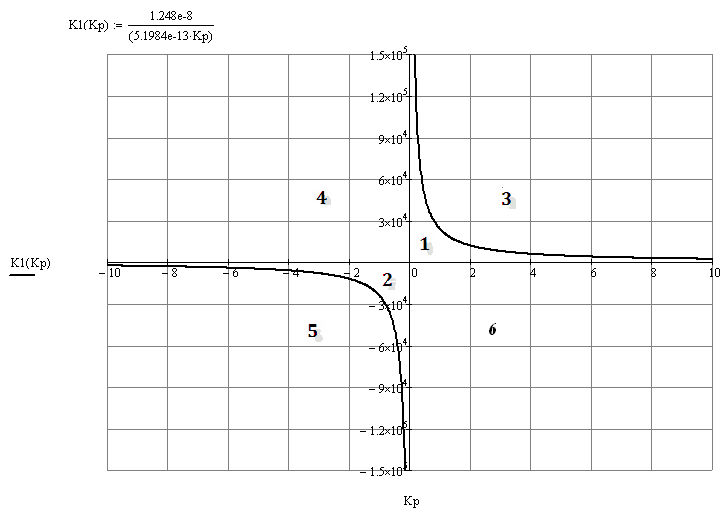
Таким образом получили 6 областей. Найдем в каких областях САУ устойчиво: для этого из каждой области возьмем по одной точке и воспользовавшись критерием устойчивости Гурвица проверим каждую область.
Критерий устойчивости Гурвица:
|
|
|
Необходимым и достаточным условием устойчивости является положительность определителя Гурвица и всех его диагональных миноров.
1область Кр=1, К1=1
Получаем следующие значения коэффициентов

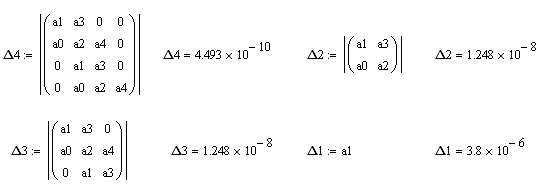
Все определители положительны, поэтому САУ в этой области устойчива.
Для проверки найдем корни уравнения:

Вещественные части всех корней получились отритцательными, что подтверждает устойчивость

2 область Кр=-1, К1=-1
Получаем следующие значения коэффициентов

Все определители положительны, поэтому САУ в этой области устойчива.
Для проверки найдем корни уравнения:
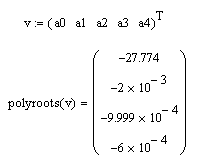
Вещественные части всех корней получились отритцательными, что подтверждает устойчивость
3 область Кр=2, К1=30000
Получаем следующие значения коэффициентов

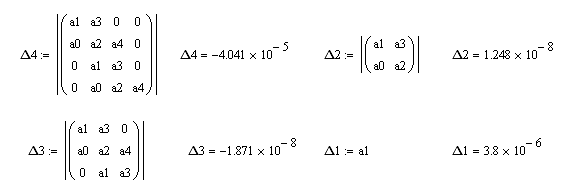
Не все определители положительны, поэтому система в этой области неустойчива
Корни уравнения:

Есть корень с положительной вещественной частью, что говорит о том, что система в данной области неустойчива.
4 область Кр=-1, К1=1
Получаем следующие значения коэффициентов

а4<0, Не все коэффициенты характеристического полинома одного знака, поэтому пользуясь необходимым условием устойчивости Стодола, можно сказать что в этой области система неустойчива.
5 область Кр=-2, К1=-30000
Получаем следующие значения коэффициентов


Не все определители положительны, поэтому система в этой области неустойчива
Корни уравнения:

Есть корень с положительной вещественной частью, что говорит о том, что система в данной области неустойчива.
6 область Кр=1, К1=-1
Получаем следующие значения коэффициентов

а4<0, Не все коэффициенты характеристического полинома одного знака, поэтому пользуясь необходимым условием устойчивости Стодола, можно сказать что в этой области система неустойчива.
|
|
|
Таким образом устойчивыми областями является первая и вторая.
|
|
|


