 |
Выполнение задания при использовании для динамического расчета балки системы с несколькими степенями свободы
|
|
|
|
Расчет на ПК с использованием программы SCAD
В варианте 1.1. задания 1 было рассмотрено решение задачи об определении максимального прогиба железобетонной балки с электродвигателем, расположенным по ее длине. Расчет выполнялся от двух статических и одного динамического загружений по расчетной схеме балки в виде системы с одной степенью свободы.
Рассмотрим решение этой же задачи с использованием расчетной схемы МКЭ, когда балка по длине пролета разделена на 4 равных конечных элемента типа 2. В этом случае при загружении узла 3 динамической нагрузкой получим расчетную схему в виде системы с тремя степенями свободы, которая может быть представлена в виде, приведенном на рис. 4.
Рис. 4
Результаты расчета:
------------------------------------------------------------------------------------------
| Р А С П Р Е Д Е Л Е Н И Е В Е С О В М А С С |
------------------------------------------------------------------------------------------
| 1 2 3 4 5 |
------------------------------------------------------------------------------------------
| 3 - (гарм-3) |
| Z 1.067 2.597 1.067 |
------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------|
|Загpу: N: COБCTB.: Ч A C T O T Ы : ПEPИOДЫ |
|: П/П: :-----------------------------:-------------- -|
|жение:: ЗHAЧEHИЯ: 1/C: ГЦ: C |
------------------------------------------------------------------------
| 3 1.009285 107.7001 17.1497 .05831 |
| 2.0017818 561.2033 89.36359 .0111902 |
|
|
|
| 3.0012916 774.1783 123.2768 .0081118 |
------------------------------------------------------------------------
Ая СФК
Ая СФК
Я СФК
------------------------------------------------------------------------------------------
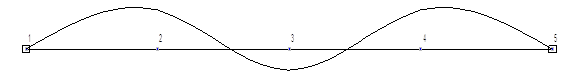
| И Н Е Р Ц И О Н Н Ы Е Н А Г Р У З К И |
------------------------------------------------------------------------------------------
| 1 2 3 4 5 |
------------------------------------------------------------------------------------------
| 3 - 1 (гарм-3) |
| Z .0665.8888.0665 |
| 3 - 2 |
| Z -.0152 -.1125 -.0152 |
------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------
| П Е Р Е М Е Щ Е Н И Я У З Л О В |
------------------------------------------------------------------------------------------
| 1 2 3 4 5 |
------------------------------------------------------------------------------------------
| 1 - (СВ) |
| Z -.445676 -.62551 -.445676 |
| 2 - (Вес двиг.) |
| Z -.245535 -.357142 -.245535 |
| 3 - 1 (гарм-3) |
| Z -.158161 -.228817 -.158161 |
| 3 - 2 |
|
|
|
| Z .021624.03117.021624 |
------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------
| У С И Л И Я /НАПРЯЖЕНИЯ/ В ЭЛЕМЕНТАХ |
------------------------------------------------------------------------------------------
| 2_ 1-1 1-2 2-1 2-2 3-1 3-2 4-1 4-2 |
| 1 1 2 2 3 3 4 4 |
| 2 2 3 3 4 4 5 5 |
------------------------------------------------------------------------------------------
| 1 - (СВ) |
| M 2.81367 2.81367 3.75156 3.75156 2.81367 2.81367 |
| 2 - (Вес двиг.) |
| M 1.33875 1.33875 2.6775 2.6775 1.33875 1.33875 |
| 3 - 1 (гарм-3) |
| M .894092.894092 1.6718 1.6718.894092.894092 |
| 3 - 2 |
| M -.125189 -.125189 -.223664 -.223664 -.125189 -.125189 |
| 3 - S1 |
| M .902814.902814 1.6867 1.6867.902814.902814 |
------------------------------------------------------------------------------------------
Рис. 5
Расчет вручную. Исходными данными для расчета вручную считаем определенные в результате модального анализа СЧ и СФК для рассматриваемой балки как системы с тремя степенями свободы.
Вычисление векторов инерционных сил в СФК
Вычисление для первой СФК (i=1)
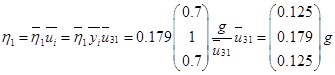
Вычисление для первой СФК (i=3)
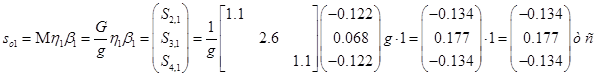
Результаты расчета сведем в таблицу 1.
Таблица 1
| 
| 
| 
| 
| 
|
| 1 | 0.179 |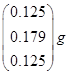 
| 
| 1.517 | 
|
| 2 | 0 | 
|
| 
| 
|
| 3 | -0.136 | 
| 
|
| 
|
2. Выполнение контроля разложения вектора 
по СФК
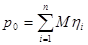
В данном случае проверка выполняется.
3. Вычисление перемещений и усилий в СФК в любом сечении 
балки
Вектору инерциональных нагрузок 
соответствует вектор прогибов балки 
и усилия 
в любом сечении 
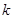. Для сокращения ручных вычислений ограничимся вычеслением прогиба и изгибающего момента только в среднем сечении балки. Результаты расчета сведем в таблицу 2.
Таблица 2
| 
| 
|
| 1 | 
| 
|
| 2 | 0 | 0 |
| 3 | 
| 
|
|
|
|
Сопоставление суммарного вектора инерционных нагрузок по всем СФК
Этот вектор во всех СФК (при 
) определяется при синусе равном 1.
тс.
В приведенной таблице результатов расчета инерционных сил в программе SCAD приводятся не векторы 
СФК, а векторы 
и 
. Тогда расчетный вектор вычислим по формуле:
тс.
Как видим, результаты практически совпали.
Вычисление расчетного изгибающего момента в среднем сечении балки
Суммирование амплитудных значений изгибающего момента, вычисленных в среднем сечении балки для всех трех СФК выполняется по формуле:
тс*м
В программе SCAD:
тс*м
Расчеты, выполненные в программе SCAD и вручную практически совпадают.
Сопоставления результатов расчета по двум расчетным схемам
Сопоставление результатов расчета рассматриваемой балки по определению её максимального прогиба и максимального изгибающего момента по рассмотренным 2 расчетным схемам показывает, что даже использование для динамического расчета расчетной схемы с одной степенью свободы дает удовлетворительные результаты.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Константинов И.А., Лалина И.И. Строительная механика. Расчет стержневых систем. Учеб. пособие. СПб.: Изд-во Политехн. ун-та. 2005. 155 с.
2. Константинов И.А. Строительная механика. Использование программы SCAD для расчета стержневых систем. Ч.I: Учеб. пособие. СПб.: Изд-во СПбГПУ, 2004. 81с.
3. Константинов И.А., Лалина И.И. Строительная механика. Использование программы SCAD для расчета стержневых систем. Ч.2: Учеб. пособие. СПб.:Изд-во Политехн. ун- та, 2005. 82с.
4. Лалин В.В., Константинов И.А., Лалина И.И.Динамика сооружений. Использование программы SCAD для решения задач динамики сооружений. Ч.1: Сайт каф. ЭиПГС, ФОДО,
2005. 92с.
|
|
|
