 |
Расчет по предельным состояниям второй группы
|
|
|
|
Определение геометрических характеристик
Геометрические характеристики приведенного сечения определяем по расчетному сечению (см. рис. 13).
Находим площадь приведенного сечения:
здесь 
отсюда
Статический момент площади приведенного сечения относительно нижней грани (см. рис. 13):
,
где 
Таким образом,
Момент инерции приведенного сечения относительно его центра тяжести вычислим по формуле:
где 
;
отсюда
Рассчитываем момент сопротивления приведенного сечения:
- относительно нижней грани
- относительно верхней грани
,
здесь 
Находим упругопластический момент сопротивления:
- относительно нижней грани
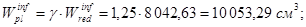
- относительно верхней грани
При 
коэффициент 
1,25.
Определяем радиусы инерции:
;
.
Определение потерь предварительного напряжения
Способ натяжения арматуры электротермический.
Находим первые потери:
Потери от релаксации напряжений в арматуре
.
Потери от температурного перепада в агрегатно-поточной технологии отсутствуют, поэтому 
.
Потери от деформации формы учитываются в расчете требуемого удлинения при электротермическом натяжении, поэтому 
.
Потери от деформации анкеров учитываются при расчете удлинения, поэтому 
.
Следовательно, 
Усилие предварительного обжатия с учетом первых потерь
Определяем вторые потери:
- от усадки бетона
;
- от ползучести бетона
,
где 
– коэффициент ползучести бетона, при классе бетона В20 и нормальной влажности 40–75% 
;
;
;
Отсюда
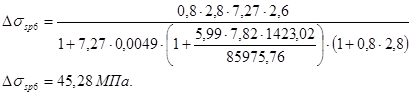
Суммарные потери
Потери напряжений округляем до 5 МПа. Тогда 
.
|
|
|
Усилие в арматуре с учетом всех потерь:
Расчет трещинообразования на стадии эксплуатации
Находим момент трещинообразования:
.
С учетом того, что 
получим:
.
Следовательно, от нормативных нагрузок трещины образуются.
Расчет по раскрытию нормальных трещин
Ширину раскрытия нормальных трещин определяем по формуле:
.
Рассчитаем ширину 
раскрытия трещин при действии постоянных и длительных нагрузок (от действия 
). При продолжительном действии нагрузки 
; для арматуры периодического профиля 
; для изгибаемых элементов 
; предварительно назначаем 
.
,
где 
, так как центр усилия совпадает с центром тяжести растянутой арматуры; 
;
, тогда
.
Определяем базовое расстояние между трещинами 
. Для этого найдем площадь растянутого бетона 
:
;
, поэтому принимаем 
; тогда площадь растянутого бетона
Отсюда
.
Поэтому принимаем 
.
Получаем:
.
Рассчитаем ширину 
раскрытия трещин от кратковременного действия полного момента 
. При непродолжительном действии нагрузки 
. Остальные коэффициенты и те же, что и для 
.
.
Получаем:
.
Рассчитаем ширину 
раскрытия трещин от кратковременного действия момента от постоянных и длительных нагрузок. При непродолжительном действии нагрузки 
. Остальные коэффициенты и 
те же, что и для 
; 
. Получаем:
.
Полную ширину раскрытия трещин (при непродолжительном раскрытии) рассчитываем по формуле:
Трещиностойкость обеспечена.
Расчет прогибов
При расчете жесткости необходимо определить прогиб для плит, загруженных равномерной нагрузкой и полную кривизну 
для элементов с трещинами.
Поскольку рассчитываем пустотную плиту, а деформации таких плит нормируются эстетическими требованиями, то полную кривизну определяем:
.
Так как 
, то кривизну от продолжительного действия постоянной и длительной нагрузки 
допускается определять:
|
|
|
Коэффициент 
находим в зависимости от 
, 
, 
:
;
;
,
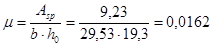где 
(принимаем 
);
(при продолжительном действии нагрузки 
), следовательно,
;
;
;
.
Таким образом, по полученным данным находим по т. 4,5 [5]: 
.
Кривизну, обусловленную остаточным выгибом вследствие усадки и ползучести бетона от усилия обжатия, определяем по формуле:
,
где 
; 
находим при
тогда
Отсюда
Теперь мы можем рассчитать кривизну 
:
.
Проверим, соблюдается ли условие
.
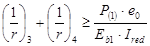Для этого вычислим следующее:
.
,
где 
.
Условие соблюдается:
.
Вычисляем полную кривизну:
;
и полный прогиб:
.
Так как 
, то жесткость плиты по эстетическим требованиям не обеспечена.
|
|
|
