Главная | Обратная связь | Поможем написать вашу работу!

ЛЕКЦИЯ 8. Примеры программ с использованием OpenGL

Имитация трехмерного ландшафта

Описываемая программа имитирует перемещение камеры над трехмерным ландшафтом. Для построения поверхности используется карта высот, хранящаяся в виде полутонового BMP-файла. Поверхность изображается как набор клеток со сторонами фиксированного размера, углы которых расположены на немного разной высоте. На клетки накладывается текстура, имитирующая травяную растительность. Камера перемещается на постоянной высоте над поверхностью.

Форма поверхности без наложения текстур показана на рис. 8.1. Прямоугольные клетки поверхности отображаются в виде двух треугольников (рис. 8.2), т.к. углы клетки чаще всего не лежат в одной плоскости.


Рис. 8.1. Поверхность, сформированная из треугольных граней.	Рис. 8.2. Разбиение квадратной клетки поверхности на два треугольника.

На каждый треугольник накладывается текстура травы (рис. 8.3).


Рис. 8.3. Изображение текстуры травы.	Рис. 8.4. Карта высот и связанная с этим изображением система координат.

Рельеф поверхности описывается с помощью функции, задающей высоту каждого угла каждой клетки. Эта функция задается с помощью полутонового изображения – карты высоты (рис. 8.4), каждый пиксел которой соответствует углу одной из клеток поверхности. Значения компонент изображения RGB лежат в диапазоне от 0 до 255, и именно эти значения принимаются за значения высоты в углах клеток.

Положение камеры задается в системе координат, связанной с картой высоты (рис 4). Параметры положения описываются следующей структурой:

struct CameraData {

double x, y; // Координаты камеры в системе координат

// изображения карты высот

double x_frac, y_frac; // Координаты камеры внутри клетки

// поверхности размером FLATSCALERxFLATSCALER

// Левый нижний угол этой клетки

// соответствует точке (int(x), int(y))

// на карте высот

double height; // Высота камеры над поверхностью

double mounth; // Высота поверхности в точке (x, y)

};

Первоначально камера располагается в центре карты высот. При изменении положения камеры в фоновой функции координата x изменяется так, чтобы камера перемещалась в положительном направлении оси OX. Перед рисованием ландшафта производится вычисление координат камеры внутри клетки и высоты поверхности в точке (x, y), т.к. эта точка не обязательно попадает в пиксел карты высот, а может располагаться "между пикселами". Для сокращения времени рисования отображаются не все клетки поверхности, а только те, которые попадают в видимый объем.

Задание 1.1

Текст программы находится в файле prg8_1.cpp, изображение текстуры травы хранится в файле grass.bmp, карта высот – в файле land.bmp. Cкомпилируйте программу, запустите ее и затем разберитесь в исходном тексте с помощью комментариев и приведенного выше описания.

Измените программу так, чтобы с помощью клавиш курсора можно было регулировать скорость перемещения и направление движения камеры.

2. Объемный "тетрис"

Прототипом описываемой программы является игра "BlockOut" (LDW Inc., 1989). В стакан в виде прямоугольного параллелепипеда равномерно падают блоки 8-ми типов. В каждый момент времени существует только один падающий блок. Стакан и блок состоят из единичных кубических ячеек. Блок можно перемещать параллельно дну стакана клавишами курсора и поворачивать относительно трех координатных осей буквенными клавишами Q, W, E. По нажатию пробела блок совершает быстрое падение на дно стакана. Заполненные уровни (слои ячеек) из стакана исчезают, а вышележащие слои при этом опускаются вниз.

Выберем стакан с квадратным дном размером 5х5 и высотой 12 ячеек. Расположим стакан в мировой системе координат так, как показано на рис. 8.5. При рисовании на всех стенках стакана, кроме открытой верхней стенки, рисуются тонкие вспомогательные линии для отображения ячеек (на рис. 8.5 эти линии показаны только на дне стакана). В программе содержимое стакана описывается трехмерным массивом:

int data[GLASS_H][GLASS_SZ][GLASS_SZ];

Первый индекс массива соответствует направлению оси Y, второй – оси X, третий – оси Z в системе координат стакана (рис. 8.5). Нулевое значение элемента массива соответствует пустой ячейке, единичное – заполненной.

Рис. 8.5. Система координат, связанная со стаканом (совпадает с мировой системой координат).

Падающий блок описывается трехмерным массивом ячеек 3х3х3. С этим массивом связана локальная система координат блока (рис. 8.6). Текущее положение блока внутри стакана указывается путем задания положения системы координат блока в системе координат стакана.

Рис. 8.6. Локальная система координат блока (показан массив, описывающий T-образный блок).

Таким образом, для описания падающего блока в программе предназначены две переменные – описание блока и его текущие координаты:

int fallingBlock[3][3][3]; // Ячейки блока [y][x][z]

int fallingCoords[3]; // Координаты хранятся в виде (y,x,z)

Возможные типы блоков показаны на рис. 8.7.

Рис. 8.7. Различные типы блоков для объемного "тетриса".

В начале программы выполняется регистрация нескольких обработчиков событий. Обработчик перемещения мыши при нажатой левой кнопке применяется для изменения положения камеры. Сначала камера направлена на центр стакана параллельно отрицательному направлению оси OZ. Камеру можно перемещать по дуге окружности постоянного радиуса вокруг центра стакана (рис. 8.8).

Рис. 8.8. Дуга окружности, по которой с помощью мыши можно перемещать камеру. Точка G_c – центр стакана, C₀ – начальное положение камеры.

Обработчики клавиш курсора позволяют перемещать блок на 1 ячейку параллельно осям системы координат стакана. Обработчик клавиши "пробел" выполняет падение блока на дно стакана. Буквенная клавиша 'Q' производит поворот блока на 90 градусов вокруг оси, параллельной оси OX и проходящей через центр блока. Клавиши 'W' и 'E' выполняют аналогичные повороты вокруг осей, параллельных осям OZ и OY.

Подробнее рассмотрим выполнение поворота блока. На рис. 8.9 приведены иллюстрации, поясняющие поворот блока вокруг оси, проходящей через центр массива ячеек параллельно оси OX. Трехмерный массив, описывающий блок, разбивается в направлении оси OX на 3 квадратные матрицы. Для поворота блока на 90 градусов надо выполнить транспонирование каждой матрицы (поменять местами строки и столбцы). На рис. 8.9 показано преобразование средней матрицы исходного массива для T-образного блока при двух последовательных поворотах.

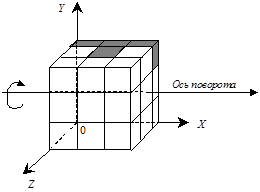
Рис. 8.9. Два поворота блока вокруг оси, параллельной оси OX.

При отсутствии событий от клавиатуры и мыши программа должна выполнять равномерное падение блока на дно стакана. Это делается с помощью фоновой функции. Скорость падения примерно равна 1 ячейка/сек. Если блок достигает дна стакана или останавливается, зацепившись за какие-либо заполненные ячейки, то программа выполняет удаление заполненных слоев ячеек и генерацию нового падающего блока.

void CALLBACK idle()

{

if (fBlockPresent)

{

static time_t prev_t;

if (time(NULL) - prev_t >= 1.0)

{

stepBlock();

prev_t = time(NULL);

}

else

{

deleteFilledLayers();

createNewBlock();

}

draw();

}

Задание 2.1

Cкомпилируйте программу prg8_2.cpp, запустите ее и затем разберитесь в исходном тексте с помощью комментариев и приведенного выше описания.

Измените функцию отображения содержимого стакана так, чтобы ячейки каждого слоя рисовались своим цветом. Цвета уровней не должны совпадать с цветами падающих блоков. Цвета уровней могут периодически повторяться, например, можно использовать всего 5-6 цветов. Для хранения значений цветов уровней заведите специальный массив.

Задание 2.2

Модифицируйте функцию генерации нового блока так, чтобы она создавала блоки 8-ми различных типов (рис. 8.7).

Задание 2.3

Добавьте в программу обработчик нажатия клавиши 'W' для поворота падающего блока вокруг оси, параллельной OZ.

Задание 2.4

Внесите в программу обработчики для пары клавиш, позволяющих приближать и удалять камеру от стакана.

Литература

1) McReynolds T., Blythe D. Advanced Graphics Programming Techniques Using OpenGL. SIGGRAPH `98 Course, 1998. (Конспекты учебного курса по неочевидным вопросам использования OpenGL для программистов, уже имеющих опыт работы с OpenGL). http://www.sgi.com/Technology/OpenGL/advanced_sig98.html

2) Neider J., Davis T., Woo M. OpenGL Programming Guide. Addison-Wesley, 1993. (Руководство по OpenGL, написанное авторами из компании Silicon Graphics – основного разработчика этой библиотеки).

3) Rogerson D. OpenGL I-VIII: Technical Articles. MSDN, December 1994–May 1995. (Технические статьи, описывающие различные аспекты использования OpenGL в программах для Windows.)

4) Коваленко В. OpenGL - что дальше? (Статья, описывающая некоторые недостатки OpenGL и устраняющей эти недостатки библиотеки OpenGL Optimizer). http://madli.ut.ee

5) Подобедов Р. Что такое OpenGL? (Статья с описанием основных характеристик OpenGL и некоторых конкурирующих библиотек). http://madli.ut.ee

6) Тарасов И. Библиотека OpenGL. 1999. (Электронный вариант книги-самоучителя) http:\\www.citforum.ru\programming\opengl\index.shtm

7) Фоли Д., Вэн Дэм А. Основы интерактивной машинной графики. в 2-х кн. М.: Мир, 1985 г. (Монография, посвященная алгоритмам двумерной и трехмерной компьютерной графики и структуре графических программ).

Учебно-методическое издание

А.А. Богуславский, С.М. Соколов

Основы программирования на языке Си++

В 4-х частях.

(для студентов физико-математических факультетов

педагогических институтов)

Компьютерная верстка Богуславский А.А.

Технический редактор Пономарева В.В.