 |
Методы выявления автокорреляции
|
|
|
|
Графический метод
По формальному признаку можно заподозрить автокорреляцию в модели, если t-статистика неправдоподобно высока. Анализ графической зависимости отклонений от наблюдаемой автокорреляции установлен при сравнительном графическом отклонении с известными функциями.
Построим корреляцию с помощью RESID модели VK и лагом этой же модели RESID (-2):
Рисунок 1. Корреляционное поле
В итоге мы видим распределение точек:
четверть - 12
четверть - 8
четверть - 10
четверть - 8.
По этим данным с полной уверенностью нельзя сказать есть ли корреляция, т.к. данные распределены достаточно равномерно, но всё же есть вероятность, из-за преобладания точек в 1 и 3 четвертях.
Метод Дарбина-Уотсона
Наиболее известным критерием обнаружения автокорреляции первого порядка является критерий Дарбина-Уотсона.
Статистика Дарбина-Уотсона является важнейшей характеристикой качества регрессионной модели.
Суть его состоит в вычислении статистики Дарбина-Уотсона и на основе ее величины - осуществлении выводов об автокорреляции:
Статистика Дарбина-Уотсона тесно связана с выборочным коэффициентом корреляции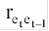 
:
Таким образом, 0 
DW 4 и его значения могут указать на наличие либо отсутствие автокорреляции.
Если выборочный коэффициент корреляции равен 0 (автокорреляция отсутствует), то DW = 2.
Если выборочный коэффициент корреляции равен 1 (положительная автокорреляция), то DW = 0.
Если выборочный коэффициент корреляции равен - 1 (отрицательная автокорреляция), то DW = 4.
Разработаны специальные таблицы критических точек статистики Дарбина-Уотсона, позволяющие при данном числе наблюдений n, количестве объясняющих переменных m и заданном уровне значимости 
определять границы приемлемости (критические точки) наблюдаемой статистики DW.
|
|
|
Для заданных n, m, в таблице указывается два числа: d 
- верхняя граница и d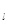 
- нижняя граница.
Выводы осуществляются по следующей схеме.
Если DW < d 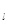, то это свидетельствует о положительной автокорреляции остатков.
Если DW > 4 - d 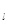, то это свидетельствует об отрицательной автокорреляции остатков,
При d < DW < 4 - d , гипотеза об отсутствии автокорреляции остатков принимается.
Если d 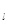< DW < d или 4 - d < DW < 4 - d 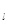, то гипотеза об отсутствии автокорреляции не может быть ни принята, ни отклонена.
Не обращаясь к таблице критических точек Дарбина-Уотсона, можно пользоваться "грубым" правилом и считать, что автокорреляция остатков отсутствует, если 1,5 < DW < 2,5. Для более надежного вывода следует обращаться к таблицам.
При наличии автокорреляции остатков полученное уравнение регрессии обычно считается неудовлетворительным.
Нужно отметить, что при использовании критерия Дарбина-Уотсона необходимо учитывать следующие ограничения:
1) Критерий DW применяется лишь для тех моделей, которые содержат свободный член.
2) Предполагается, что случайные отклонения определяются по следующей итерационной схеме: 
, называемой авторегрессионной схемой первого порядка АR (1). Здесь V 
- случайный член.
) Статистические данные должны иметь одинаковую периодичность, т.е. не должно быть пропусков в наблюдениях.
) Критерий Дарбина-Уотсона не применим для регрессионных моделей, содержащих в составе объясняющих переменных зависимую переменную с временным лагом в один период, т.е. для так называемых авторегрессионных моделей вида:
Для авторегрессионных моделей разработаны специальные тесты обнаружения автокорреляции, в частности h-статистика Дарбина, которая определяется по формуле:
|
|
|
где 
- оценка автокорреляции первого порядка,
D (g) - выборочная дисперсия коэффициента при лаговой переменной у 
,- число наблюдений.
При большом объеме выборки n и справедливости нулевой гипотезы Н 
: 
=0 статистика h имеет стандартизированное нормальное распределение (h ~ N (0, 1)). Поэтому по заданному уровню значимости определяется критическая точка 
из условия 
и сравнивается h с 
. Если 
, то нулевая гипотеза об отсутствии автокорреляции должна быть отклонена. В противном случае она не отклоняется,
Обычно значение рассчитывается по формуле 
, а D (g) равна квадрату стандартной ошибки оценки g коэффициента 
. Поэтому h легко вычисляется на основе данных оцененной регрессии.
Основная проблема с использованием этого теста заключается в невозможности вычисления h при nD (g) > 1.
Согласно данным, полученным в Eviews, наблюдаемая точка DW = 1.375019
Затем, опираясь на данные, что количество объясняющих переменных в уравнении регрессии m=4, a объем выборки n=40, находим критические точки по таблице распределения Дарбина-Уотсона:
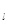= 1.285, d =1.721
Согласно полученным данным, нарисуем следующую схему:
Следовательно, гипотеза об отсутствии автокорреляции первого порядка не может быть ни принята, ни отклонена.
Метод Сведа-Эйзенхарта
В методе необходимо подсчитать количество положительных и отрицательных отклонений, а также выделить в ряду отклонений подрядов последовательных отношений имеющих один знак. Количество таких подрядов обозначить "к".
При использовании метода рядов последовательно определяются знаки отклонений е 
. Ряд определяется как непрерывная последовательность одинаковых знаков. Количество знаков в ряду называется длиной ряда.
Визуальное распределение знаков свидетельствует о неслучайном характере связей между отклонениями. Если рядов слишком мало по сравнению с количеством наблюдений n, то вполне вероятна положительная автокорреляция. Если же рядов слишком много, то вероятна отрицательная автокорреляция.
Для более детального анализа предлагается следующая процедура. Пусть:
· n - объем выборки;
· n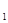 
- общее количество знаков "+" при n наблюдениях (количество положительных отклонений е );
|
|
|
· n 
- общее количество знаков " - " при n наблюдениях (количество отрицательных отклонений е );
· к - количество рядов.
При достаточно большом количестве наблюдений (n 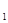|> 10, n 
> 10) и отсутствии автокорреляции мы имеем асимптотически нормальное распределение с
Тогда, если:
то гипотеза об отсутствии автокорреляции не отклоняется.
При небольшом числе наблюдений (n 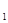|> 20, n > 20) Свед и Эйзенхарт разработали таблицы критических значений количества рядов при n наблюдениях.
Суть таблиц заключается в следующем.
На пересечении строки n 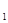и столбца n определяются нижнее к 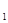и верхнее к 
значения при уровне значимости 5%.
Если к 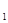< к < к 
, то говорят об отсутствии автокорреляции.
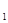Если к к , то говорят о положительной автокорреляции остатков.
Если к 
к , то говорят об отрицательной автокорреляции остатков,
Этот метод основан на определении знаков отклонений RESID (см. Приложение Б).
На примере нашей модели:
"+", 6"-", 7"+", 7"-", 2"+", 5"-", 2"+",2"-", 6"+" при 40 наблюдениях.
Рядом называется непрерывная последовательность одинаковых знаков, то есть количество рядов в данной модели k=11.
По таблице критических значений количества рядов при n наблюдениях определяем нижнее k1 = 2 и верхнее k2 = 9. Наша переменная k = 9 находится в промежутке k1 < k < k2, что говорит об отсутствии автокорреляции или о её слабом проявлении.
Заключение
В данной работе был произведен анализ построения эконометрической модели и исследования проблемы автокорреляции случайных отклонений с помощью теста Сведа-Эйзенхарта, статистики Дарбина-Уотсона и графического метода. Все эти подходы дополняют друг друга. Первоначальный анализ коррелограммы остатков позволяет определить наиболее вероятный порядок серийной корреляции, если она существует. Для критического уровня значимости α = 5% коэффициенты при экзогенных переменных являются статистически значимыми. В целом модель оказалась качественной, адекватной, в ней отсутствует мультиколлинеарность, ошибки распределены по нормальному закону. Ее недостатком является завышенная F-статистика.
|
|
|
|
|
|
