 |
Моделирование при помощи булева вычитания
|
|
|
|
Булевы операции вычитания наиболее широко используются при моделировании. Чаще всего они применяются для создания закруглений и углублений на первом из исходных объектов, а также выемок и сквозных отверстий в нем, и потому второй объект условно можно считать своеобразной стамеской или фрезой, которая создает желобок на первом объекте или выбирает какую-то его часть. В качестве «режущих инструментов» могут быть задействованы самые разные объекты, в частности объекты, полученные из криволинейных сплайнов путем лофтинга или вращения.
На первом этапе воспользуемся булевой операцией вычитания для формирования цилиндрического отверстия внутри шара. Создайте исходные объекты в виде шара и цилиндра (радиус сечения цилиндра должен быть меньше радиуса шара, а его длина — больше радиуса шара) и выровняйте их друг в отношении друга по осям X, Y и Z, применив операцию Align (Выровнять) (рис. 9). Проведите рендеринг и сразу же скорректируйте параметры объектов так, чтобы они оказались достаточно гладкими, особенно в области пересечения; если этого не сделать, то созданный булев объект тоже не будет иметь надлежащей гладкости. В данном случае видно (рис. 10), что степень гладкости требуется увеличить — это достигается путем повышения плотности объектов: увеличения количества сегментов и сторон сегментов и уменьшения размера сегментов (рис. 11). В то же время при работе со сложными моделями для ускорения процесса моделирования в ряде случаев лучше увеличивать плотность объектов, задействованных в качестве операндов, не перед созданием булевой операции, а после — в ходе редактирования операндов на уровне объектов.

Рис. 9. Шар и цилиндр
|
|
|

Рис. 10. Рендеринг исходных объектов

Рис. 11. Рендеринг объектов и их параметры после корректировки гладкости
Выделите цилиндр, установите режим создания булевых объектов, установите операцию Subtraction (B-A) (Вычитание B-A), для указания операнда B щелкните по кнопке Pick Operand B (Выбрать операнд B) и укажите сферу. Это приведет к удалению внутренней части сферы точно по размеру исходного цилиндра таким образом, что в сфере появится сквозное отверстие (рис. 12).

Рис. 12. Сфера с отверстием
Формируемые при помощи булева вычитания отверстия могут иметь самую разную форму, а результат зависит не только от размеров и формы объектов, но и от положения их в отношении друг друга, а также от того, какой из объектов был указан первым. Возьмите в качестве исходных объектов куб и шар и разместите их показанным на рис. 13 образом. Выделите куб, установите в режиме создания булевых объектов операцию Subtraction (A-B) и в качестве операнда B укажите сферу — результатом станет появление в ней соответствующего углубления (рис. 14), а потом сохраните результат (он нам позже потребуется). Отмените созданную булеву операцию и примените к исходным объектам булево вычитание Subtraction (A-B), но в качестве первого операнда укажите сферу — и вместо куба с углублением итогом операции окажется шар, в котором как бы вырезана одна из его четвертей (рис. 15). Стоит отметить, что для получения того же самого результата совсем не обязательно было менять местами операнды: с таким же успехом можно было вместо операции Subtraction (A-B) выбрать операцию Subtraction (B-A). Подобная взаимозамена операций Subtraction (A-B) и Subtraction (B-A) очень удобна, так как при неверном выборе операнда A не потребуется отменять операцию, а достаточно лишь переключиться с одной операции вычитания на другую.

Рис. 13. Куб и шар
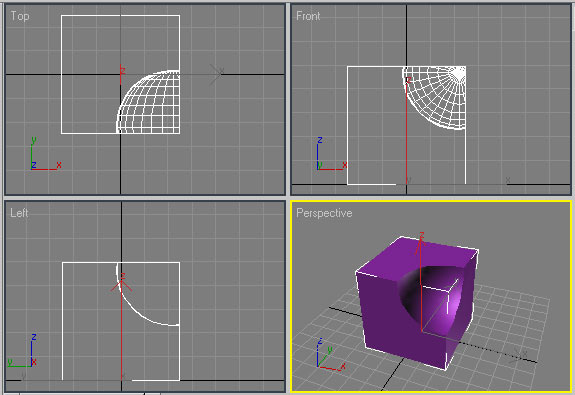
Рис. 14. Углубление в кубе

Рис. 15. Выемка фрагмента шара
Как было отмечено, форма получающейся выемки определяется вторым операндом. Попробуйте вместо шара создавать выемки и углубления другими объектами. Например, при применении объекта Hose (Шланг) (рис. 16) может быть получена резьбообразная выемка (рис. 17). Если же взять в качестве операнда B граненую призму Gengon (рис. 18), то выемка окажется многогранной (рис. 19), а при использовании веретена Spindle — скошенной (рис. 20 и 21) и т.п.
|
|
|
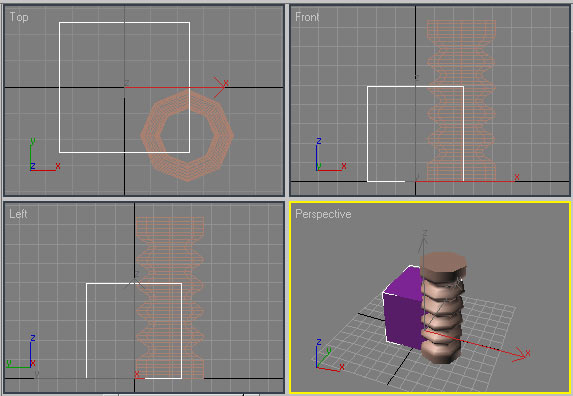
Рис. 16. Исходные объекты

Рис. 17. Куб с резьбовидной выемкой
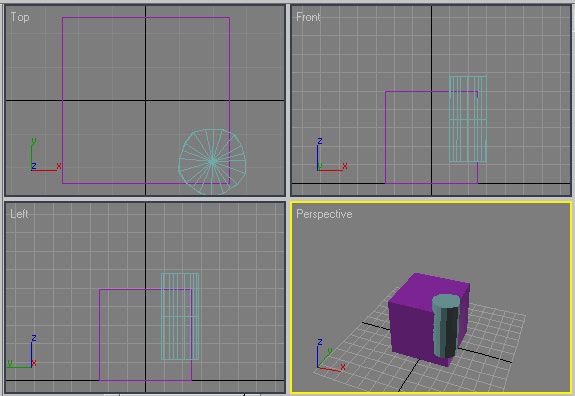
Рис. 18. Куб и шланг
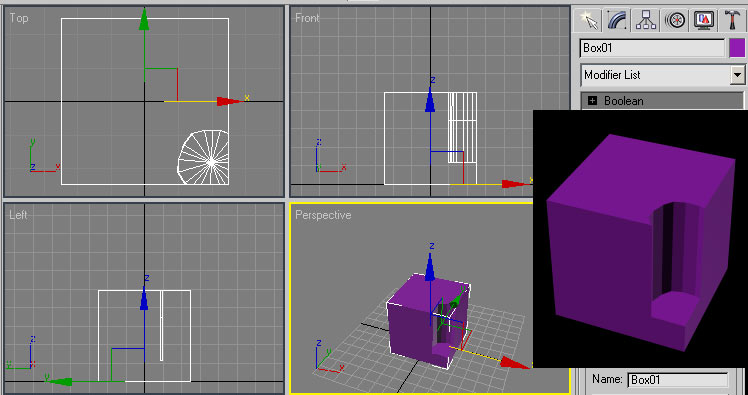
Рис. 19. Куб с граненой выемкой
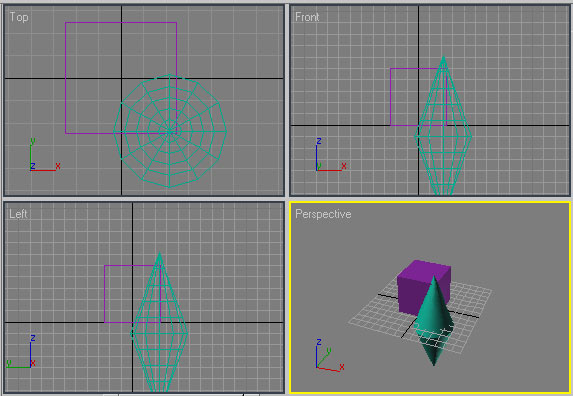
Рис. 20. Куб и веретено

Рис. 21. Куб со скошенной выемкой
Булева операция Intersection (Пересечение) является обратной к булевым операциям Subtraction (A-B)/Subtraction (B-A) (Вычитание (А-В)/Вычитание (В-А), так как получаемые с ее помощью булевы объекты представляют собой фрагменты операндов A и B, которые удаляются при операции булева вычитания, если ее провести в отношении тех же самых объектов. Возьмите в качестве исходных рассмотренные выше куб и шар, выберите куб в качестве операнда A, а затем проведите булеву операцию Intersection (Пересечение) — результатом будет получение четверти шара, которая ранее оказывалась вырезанной в ходе операции Subtraction (B-A) (рис. 22).
Рис. 22. Исходные объекты и булевы объекты при операциях Intersection и Subtraction (В-А)
Более интересные варианты поверхностей создаются при использовании в качестве операнда B скрученных объектов. Можно попробовать получить подобный объект на основе примитива Torus, в исходном состоянии имеющего такой вид, как на рис. 23, а после скручивания (параметр Twist) на 360° — как на рис. 24. Дополнительно создайте цилиндр, разместите объекты, как показано на рис. 25, и при выполнении булевой операции Subtraction (A-B) укажите цилиндр как операнд A — результат представлен на рис. 26.

Рис. 23. Исходный торус

Рис. 24. Торус после скручивания

Рис. 25. Цилиндр и скрученный торус

Рис. 26. Цилиндр с резьбой
|
|
|


