 |
Короткое замыкание в цепи с резистором и катушкой
|
|
|
|
Рис. 5.2
Исследуем электромагнитные процессы в цепи, изображенной на рис. 5.2, происходящие после замыкания ключа.
Рассчитаем установившийся режим в цепи до коммутации (до замыкания ключа) и определим из него независимое начальное условие — ток в катушке в момент t = 0-, непосредственно предшествующий коммутации
i(0-) = i(0+) = E / (Rвн + R).
Найдем установившийся ток i после коммутации. Так как во вновь образованном контуре из катушки L и резистора R нет источника, то iy = 0.
Для определения свободной составляющей тока запишем по второму закону Кирхгофа уравнение электрического состояния цепи после коммутации:
.
Характеристическое уравнение имеет вид:
pL + R = 0.
Общее решение уравнения для свободной составляющей:
iсв = A ept,
где: А – постоянная интегрирования;
p = - R/L, c-1 – корень характеристического уравнения.
Записав общий вид переходного тока катушки
i = iу + iсв = A ept,
приравниваем его значение i(0+) = A в точке t = 0+ к значению i(0-), найденному в п. 1. Получаем искомую константу
A = E / (Rвн + R) = I0.
Переходный ток i = iу + iсв при этом равен
,
где τ = L / R – постоянная времени цепи.
Постоянная времени – это время, в течение которого свободная составляющая процесса уменьшается в е = 2,72 раза по сравнению с начальным значением.
Рис. 5.3
График изменения переходного тока показан на рис. 5.3.
Определим э.д.с. самоиндукции катушки
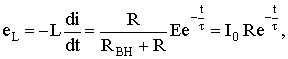t ≥ 0.
В момент коммутации эта э.д.с. равна напряжению на сопротивлении R, а в дальнейшем уменьшается по экспоненциальному закону. На основании изложенного можно сделать следующие выводы.
1. При коротком замыкании в рассматриваемой цепи ток в ней изменяется по экспоненциальному закону, уменьшаясь от начального значения до нуля.
|
|
|
2. Скорость изменения тока определяется постоянной времени цепи, которая равна индуктивности катушки, деленной на активное сопротивление цепи.
3. Практически можно считать, что переходный процесс заканчивается при t ≈ (3…5)τ, когда первоначальное значение тока уменьшается по модулю на порядок.
4. Напряжение на катушке в начальный момент времени равно напряжению на активном сопротивлении:
uL(0+) = I0R.
5. С энергетической точки зрения рассматриваемый переходный процесс характеризуется расходом энергии магнитного поля катушки на тепловые потери в резисторе. Следует отметить, что сопротивление резистора влияет не на количество выделенной теплоты W, а на начальное значение напряжения катушки и длительность процесса. В самом деле
.
Включение цепи с резистором и катушкой на постоянное напряжение
Рис. 5.4
Переходный ток в цепи, изображенной на рис. 5.4, представим в виде
i = iу + iсв.
1. До коммутации тока в катушке не было, следовательно,
iL(0-) = 0.
2. Установившаяся составляющая тока после коммутации
iу = U / R.
3. Свободная составляющая тока для цепи, описываемой дифференциальным уравнением первого порядка
iсв = A e-t/τ =A ept, p = - R / L.
4. По начальным условиям определим постоянную интегрирования А и свободную составляющую тока:
i(0) = iу(0) + iсв(0); i(0) = iу(0+) + iсв(0-);
или
0 = U / R + A; A = -U / R; iсв = -U / R · e-t/τ.
Переходный ток получается в виде
i = U / R (1 - e-t/τ).
Рис. 5.5
Напряжение на катушке
.
Кривые изменения токов i, iy, iсв и напряжения на катушке uL показаны на рис. 5.5.
При включении рассматриваемого контура под постоянное напряжение ток в нем нарастает от нуля до установившегося значения. Скорость нарастания тока
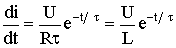
изменяется по экспоненте с отрицательным показателем. В момент t = 0 эта скорость максимальна и равна U / L [А/с], со временем она падает практически до нуля, процесс выходит на установившийся режим.
В первый после коммутации момент t = 0+ ток в цепи еще равен нулю, и напряжение на катушке максимально uL = U, далее оно экспоненциально снижается до нуля.
|
|
|
|
|
|
