 |
Тема 6. Графический метод.
|
|
|
|
График – это наглядное изображение статистический информации.
Выделяют основные виды графиков:
Гистограмма – это диаграмма, используемая для отображения данных из таблицы абсолютных частот в виде отдельных столбиков. Она используется для выявления типа распределения исследуемых данных.
Полигон – это линейный график, используемый для отображения данных относительных частот в виде ломанной линии.
Кумулянта - это линейный график, используемый для отображения данных накопленных частот в виде ломанной линии.
Секторная диаграмма – это круговая диаграмма в виде отдельных секторов, отражающих структурное изменение какого-либо явления.
Тема 7. Показатели вариации
Показатели вариации используются для измерения степени колеблемости отдельных значений признака от средней. Основные обобщающие показатели вариации: дисперсия, среднее квадратическое отклонение, коэффициент вариации.
Дисперсия признака представляет собой средний квадрат отклонений вариантов от их средней величины. В зависимости от исходных данных она вычисляется:
для несгруппированных данных по формуле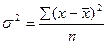 
,
для сгруппированных данных по формуле 
.
для сгруппированных данных по интервалу по формуле 
Расчеты дисперсии можно упростить, если использовать формулу 
, где 
- средний квадрат значений признака в совокупности: 
, а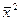 
- квадрат среднего значения признака в совокупности.
Среднее квадратическое отклонение измеряется в тех же единицах, что и варьирующий признак, показывает, на сколько в среднем отклоняются конкретные варианты признака от его среднего значения и исчисляется путем извлечения корня квадратного из дисперсии 
.
Коэффициент вариации определяется по формуле
|
|
|
.
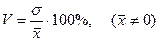Чем больше величина коэффициента вариации, тем больше разброс значений признака вокруг средней, тем менее однородна совокупность по составу. Если коэффициент вариации не превышает 30%, то совокупность считается однородной.
Тема 8. Выборочный метод в статистических исследованиях
Целью выборочного наблюдения является определение параметров генеральной совокупности (генеральной средней 
и генеральной доли 
) на основе параметров выборочной совокупности (выборочной средней 
и выборочной доли w). Разница между генеральными и выборочными параметрами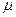 
называется ошибкой выборки. Её значение при собственно случайном и механическом отборе рассчитывается по формулам:
| Оцениваемый параметр | Повторный отбор | Бесповторный отбор |
| Средняя | 
| 
|
| Доля | 
|  
|
Предельная ошибка выборки 
определяет собой 
- кратную среднюю ошибку 
, где - коэффициент доверия, определяемый по таблице значений интегральной функции Лапласа при заданной доверительной вероятности:
| Доверительная вероятность | 0,683 | 0,950 | 0,954 | 0,990 | 0,997 |
| Коэффициент доверия | 1,00 | 1,96 | 2,00 | 2,58 | 3,00 |
Необходимая численность выборки, обеспечивающая требуемую точность расчета оценок генеральных параметров при собственно случайном и механическом отборе, определяется формулами:
| Оцениваемый параметр | Повторный отбор | Бесповторный отбор |
| Средняя | 
| 
|
| Доля |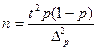 
| 
|
В приведенных формулах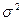 
- дисперсия признака в генеральной совокупности (или дисперсия выборочной совокупности 
, или дисперсия определенная другим возможным способом); 
- дисперсия доли в генеральной совокупности (или дисперсия доли в выборочной совокупности 
, или максимально возможная дисперсия альтернативного признака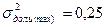 
); 
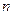- численность выборки, 
- численность генеральной совокупности.
|
|
|
