 |
Исследование точности и стабильности технологических процессов обработки
|
|
|
|
Содержание
| Лабораторная работа №1………………..………………..………………… | |
| Лабораторная работа №2………………..………………..………………… | |
| Лабораторная работа №3………………..………………..………………… | |
| Лабораторная работа №4………………..………………..………………… | |
| Лабораторная работа №5………………..………………..………………… | |
| Лабораторная работа №6………………..………………..………………… | |
| Лабораторная работа №7………………..………………..………………… | |
| Лабораторная работа №8………………..………………..………………… | |
| Лабораторная работа №9………………..………………..………………… |
Лабораторная работа №1
Исследование точности и стабильности технологических процессов обработки деталей методом большой выборки
Цель работы
Приобретение навыков исследования технологического процесса методом большой выборки.
Теоретические сведения
Методом большой выборки исследуются технологические процессы полностью устойчивые, т.е. те, у которых математическое ожидание и дисперсия исследуемого признака неизменны во времени. Большая выборка – выборка объемом N ≥ 50. Взяв выборку из 50 или более деталей, последовательно обработанных на какой-то операции механической обработки на налаженном оборудовании, производят статистический анализ относительно размера, формируемого на этой операции.
Основу статистического исследования составляет множество данных, полученных в результате измерений одного или нескольких размеров обрабатываемой детали х1,х2…хi, называемых конкретными реализациями случайной величины х.
Первым этапом исследования является графическое представление эмпирического распределения размеров обрабатываемой детали. Методика построения графического представления следующая.
|
|
|
1) Формирование ранжированного (в порядке возрастания) ряда из N исходных данных: х1,х2…хi;
2) Выявление наибольшего и наименьшего значений выборки: хmin, xmax;
3) Определение размаха варьирования выборки
4) Определение приближенного количества интервалов группирования
5) Определение величины интервала группирования ∆ х
6) Подсчет частот ni попадания случайных величин хi в интервалы группирования.
Для графического изображения эмпирического распределения размеров в выборке строится график – гистограмма.
Основные этапы исследования следующие:
- формируется интервальный ряд (хi;ni),
где хi;ni соответственно значение размера i-той детали и частость;
- Вычисляются основные характеристики: ха – математическое ожидание (среднее арифметическое) и S – выборное среднеквадратическое отклонение
Основные этапы исследования следующие:
- формируется интервальный ряд (хi;ni),
где хi;ni соответственно значение размера i-той детали и частость;
- Вычисляются основные характеристики: ха – математическое ожидание (среднее арифметическое) и S – выборное среднеквадратическое отклонение;
- вычисляются теоретические (выравнивающие) частоты nti в предположении нормального закона распределения:
- сравнивают визуально эмпирические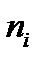 
и теоретические 
частоты построением гистограммы частот 
и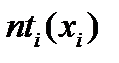 
на одном графике;
- производится проверка нулевой гипотезы, т.е. гипотезы о соответствии предполагаемого нормального распределения наблюдаемому по критериям Колмогорова и Пирсона
Исследование точности и стабильности технологических процессов обработки
Выполнить исследование точности и стабильности технологического процесса точения Ø20 
детали типа ролик на одношпиндеольном токарно-револьверном автомате.
Для выполнения такого исследования взята выборка последовательно обработанных 58 деталей. По результатам измерений наружного диаметра ролика сформирован интервальный ряд. Этот ряд имеет К=9 интервалов с шагом h=0.01 мм. Значения середин интервалов x- от 19.815 до 19.895 мм. Частоты интервалов (числа деталей, попавших в интервал) n следуют в порядке возрастания номера интервала 2,2,5,9,14,13,8,4,1. Значения середин интервалов х заданы дискретным аргументом от 19.815 с шагом 0.01, а также приведены частоты n, расчет среднего арифметического x, и среднего квадратичного отклонения S.
|
|
|
Выявляем наибольшее и наименьшее значение выборки: хmin, xmax
xmax= 23; хmin =1
Определяем размах варьирования выборки:
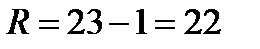
N>50 обработку эмпирических данных рекомендуется вести по значениям, сгруппированным в К непересекающихся интервалов.
Определяем приближенное количество интервалов группирования:
К = 1+ 3,3lgN
Определяем величину интервала группирования ∆ х:
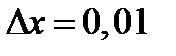
После этого строим гистограмму частот n и по виду ее делается вывод о предполагаемом теоретическом распределении, хорошо описывающем наблюдаемое, т.е. статистическое.
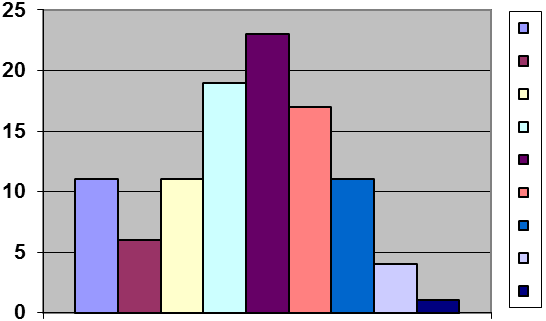
Рисунок 1.1 − Гистограмма частот
Основные этапы исследования следующие:
- формируем интервальный ряд (хi;ni),
где хi;ni соответственно значение размера i-той детали и частость;
- Вычисляем основные характеристики: ха – математическое ожидание (среднее арифметическое) и S – выборное среднеквадратическое отклонение;
,
- вычисляем теоретические (выравнивающие) частоты nti в предположении нормального закона распределения
где 
- функция плотности распределения случайной величины (размера);
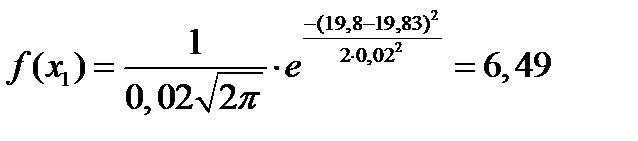
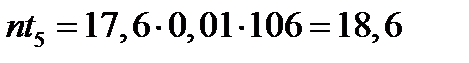
- сравниваем визуально эмпирические 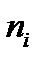и теоретические частоты построением гистограммы частот и 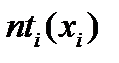на одном графике;
- производим проверку нулевой гипотезы, т.е. гипотезы о соответствии предполагаемого нормального распределения наблюдаемому по критериям Колмогорова и Пирсона
Критерий Колмогорова вычисляем следующим образом:
Расчетное значение критерия Колмогорова 
сравниваем с 
, взятым из таблиц квантилей распределения Колмогорова (Приложение 1), где Р – уровень значимости, который рекомендуется в пределах Р = 0,2…0,3. Если < , то нулевая гипотеза принимается.
|
|
|
Расчетное значение критерия Пирсона:
сравниваем с квантилями распределения Пирсона (Приложение 2), которые определяются в зависимости от Р – уровня значимости и числа степеней свободы f = K - 3. Если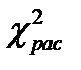 
< 
, то нулевая гипотеза принимается.
После этого проводится сравнение результатов наблюдения с требованиями чертежа. Допуск 
на размер по чертежу и достоверный диапазон рассеивания наблюдаемого размера (6×S) сравниваются вычислением коэффициента точности Кm:
Кm>1, то точность процесса не соответствует требованиям чертежа.
После этого оценивается точность настройки технологического процесса сравнением допустимой погрешности настройки 
и фактической 
:
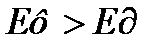, имеет место брак.
Для принятия решения об изменении технологического процесса с целью повышения точности обработки детали, вычисляется вероятность брака. Для этого находится диапазон размеров, которые выходят за поле допуска и вычисляется вероятность попадания размеров в этот диапазон (ХН…ХВ):
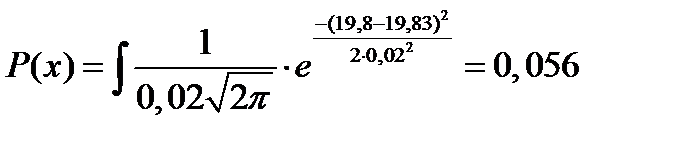
Вывод
В ходе данной лабораторной работы приобретены навыки исследования технологического процесса методом большой выборки. Ожидаемый диапазон размеров вне поля допуска составил 19,83…19,87. Вычисленная вероятность Р попадания в этот диапазон равна 0.16, т.е. ожидаемый брак составил 5,6% от деталей, протачиваемых на автомате, и чтобы отбросить брак нужно уменьшить Еф, за счет уменьшения поля допуска.
Лабораторная работа №2
Исследование точности и стабильности технологических процессов обработки детали методом малой выборки
Цель работы
Приобретение навыков исследования технологического процесса методом малой выборки.
Теоретические сведения
Малая или мгновенная выборка - это выборка, объем которой 3-7 деталей, отобранных для измерения и последовательно обработанных на исследуемой операции. За время изготовления такого небольшого количества деталей предполагается, что износ инструмента будет очень мал и не повлияет на размеры деталей в выборке. Поэтому поле рассеивания размеров деталей будет полностью определяться случайной и постоянной погрешностями.
|
|
|
Делая малые выборки через определенные промежутки времени, можно проследить не только за случайной и постоянной погрешностями в каждой выборке, но и за смещением среднего размера от выборки к выборке, т. е. за функциональной погрешностью.
Малые выборки берутся через равные промежутки времени или через равное количество деталей.
Если исследуется техпроцесс обработки наружного или внутреннего диаметров поверхности вращения, то измерения производятся таким образом, чтобы выявить со случайной и функциональной еще и постоянные погрешности. Последними чаще всего являются овальность и конусность. Овальность - обычно следствие радиального биения шпинделя станка, а конусность - непараллельности оси установки детали c направлением продольной подачи.
Измерения для выявления конусности производят в двух сечениях вдоль оси детали, а для выявления овальности - в одном сечении, но в различных радиальных направлениях.
В коротких деталях конусность чаще всего невелика, поэтому обращают внимание в основном на овальность. Идею метода малой выборки удобно рассмотреть применительно к обработке обточкой детали типа валика, показанного на рис. 2.1. Диаметр валика Х измеряется в двух сечениях I-I и II-II для выявления конусности.
Рисунок 2.1 − графики результатов измерений.
По оси абсцисс время t mm номер выборки, а по оси ординат - диаметры валика Х. Малые выборки берутся через равные промежутки времени, поэтому номера выборок находятся друг от друга на равном расстоянии. На графиках откладывают точки не каждого измерения, а только средние значения их в выборке соответственно для сечения I-I и II-II. Так, для первой выборки точка A соответствует среднему значению диаметра валика в первой выборке для сечений I-I, которые можно обозначить как 
, где первый индекс соответствует номеру выборки, а второй - номеру сечения. Для первой выборки из диаметров первого сечения рассчитывается среднее квадратическое отклонение: 
, где k - число деталей выборки, и строится достоверный диапазон рассеивания размеров, равный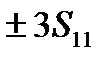 
, симметричный относительно .Затем аналогично выполняется построение для всех n-выборок. Кривая, соединяющая средние размеры 
называется линией скользящих средних сечения I-I. Такое же построение выполняется и для 2 сечения (II-II).Если предположить, что валик имеет конусность и размеры в сечении II-II больше размеров сечения I-I, то линия скользящих средних 
сечения II-II будет выше линии скользящих средних 
сечения I-I.
|
|
|
