Главная | Обратная связь | Поможем написать вашу работу!

Решение транспортной задачи

Основные шаги при решении транспортной задачи:

1. Найти начальный допустимый план.

2. Выбрать из небазисных переменных ту, которая будет вводиться в базис. Если все небазисные переменные удовлетворяют условиям оптимальности, то закончить решение, иначе к след. шагу.

3. Выбрать выводимую из базиса переменную, найти новое базисное решение. Вернуться к шагу 2.

Всякое неотрицательное решение систем линейных уравнений (2) и (3), определяемое матрицей , называется планом транспортной задачи. Опорным (базисным) планом Т-задачи называют любое ее допустимое, базисное решение.

Обычно исходные данные транспортной задачи записывают в виде таблицы.

Матрицу С называют матрицей транспортных затрат, матрицу X, удовлетворяющую условиям Т-задачи (2) и (3) называют планом перевозок, а переменные 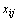- перевозками. План , при котором целевая функция минимальна, называется оптимальным.

Число переменных 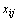в транспортной задаче с m пунктами отправления и n пунктами назначения равно m*n, а число уравнений в системах (2) и (3) равно m+n. Так как мы предполагаем, что выполняется условие (5), то число линейно независимых уравнений равно m+n–1. Следовательно, опорный план транспортной задачи может иметь не более m+n–1 отличных от нуля неизвестных.

Если в опорном плане число отличных от нуля компонент равно в точности m+n–1, то план является невырожденным, а если меньше – то вырожденным.

Как и для всякой задачи линейного программирования, оптимальный план транспортной задачи является и опорным планом.

Построение допустимого (опорного) плана в транспортной задаче

По аналогии с другими задачами линейного программирования решение транспортной задачи начинается с построения допустимого базисного плана. Существует несколько методов построения начальных опорных планов Т-задачи. Из них самый распространенный метод северо-западного угла и метод минимального элемента.

Наиболее простой способ его нахождения основывается на так называемом методе северо-западного угла. Суть метода состоит в последовательном распределении всех запасов, имеющихся в первом, втором и т. д. пунктах производства, по первому, второму и т. д. пунктам потребления. Каждый шаг распределения сводится к попытке полного исчерпания запасов в очередном пункте производства или к попытке полного удовлетворения потребностей в очередном пункте потребления. На каждом шаге q величины текущих нераспределенных запасов обозначаются а_i⁽^q), а текущих неудовлетворенных потребностей — b_j⁽^q ⁾. Построение допустимого начального плана, согласно методу северо-западного угла, начинается с левого верхнего угла транспортной таблицы, при этом полагаем а_i⁽⁰⁾= а_i, b_j⁽⁰⁾= b_j. Для очередной клетки, расположенной в строке i и столбце j, рассматриваются значения нераспределенного запаса в i -ом пункте производства и неудовлетворенной потребности j -ом пункте потребления, из них выбирается минимальное и назначается в качестве объема перевозки между данными пунктами: х_i,_j=min{а_i⁽^q), b_j⁽^q)}. После этого значения нераспределенного запаса и неудовлетворенной потребности в соответствующих пунктах уменьшаются на данную величину:

а_i⁽^q+1)= а_i⁽^q) - x_i_,_j, b_j⁽^q+1)= b_j⁽^q) - x_i_,_j

Очевидно, что на каждом шаге выполняется хотя бы одно из равенств: а_i⁽^q+1)= 0 или b_j⁽^q+1)= 0. Если справедливо первое, то это означает, что весь запас i-го пункта производства исчерпан и необходимо перейти к распределению запаса в пункте производства i+1, т. е. переместиться к следующей клетке вниз по столбцу. Если же b_j⁽^q+1) = 0, то значит, полностью удовлетворена потребность для j -го пункта, после чего следует переход на клетку, расположенную справа по строке. Вновь выбранная клетка становится текущей, и для нее повторяются все перечисленные операции.

Основываясь на условии баланса запасов и потребностей, нетрудно доказать, что за конечное число шагов мы получим допустимый план. В силу того же условия число шагов алгоритма не может быть больше, чем m+n-1, поэтому всегда останутся свободными (нулевыми) mn-(m+n-1) клеток. Следовательно, полученный план является базисным. Не исключено, что на некотором промежуточном шаге текущий нераспределенный запас оказывается равным текущей неудовлетворенной потребности (а_i⁽^q)=b_j⁽^q)). В этом случае переход к следующей клетке происходит в диагональном направлении (одновременно меняются текущие пункты производства и потребления), а это означает «потерю» одной ненулевой компоненты в плане или, другими словами, вырожденность построенного плана.

Особенностью допустимого плана, построенного методом северо-западного угла, является то, что целевая функция на нем принимает значение, как правило, далекое от оптимального. Это происходит потому, что при его построении никак не учитываются значения c_i_,_j. В связи с этим на практике для получения исходного плана используется другой способ — метод минимального элемента, в котором при распределении объемов перевозок в первую очередь занимаются клетки с наименьшими ценами.

Пример нахождения опорного плана

Поставщики	Потребители и их спрос	Мощность поставщиков

F=14 x₁₁ + 28 x₁₂ + 21 x₁₃ + 28 x₁₄ + 10 x₂₁ + 17 x ₂₂ + 15 x₂₃ + 24 x₂₄ + 14 x₃₁ + 30 x₃₂ +25 x₃₃ + 21 x₃₄

Первоначальный план получен по методу северо-западного угла. Задача сбалансированная (закрытая).

Таблица 1

Стоимость перевозок по данному плану составляет: 1681:

F=14 *27 + 28* 0 + 21*0 + 28*0 + 10 *6 + 17 *13 + 15*1 + 24 *0 + 14 *0 + 30 *0 +25*26 + 21 *17 =1681

⇐ Предыдущая 123 Следующая ⇒

Воспользуйтесь поиском по сайту: