проверка условий для получения «хороших» оценок МНК

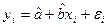Возможности применения регрессионного уравнения определяется «хорошими» свойствами оценок коэффициентов регрессии: несмещенностью, состоятельностью, эффективностью оценок. Вышеуказанные условия касаются случайной компоненты в регрессионном уравнении . Основными предположениями классической модели линейной регрессии являются следующие:

1) ,

2) , дисперсия постоянна.

3) .

Нарушение тех или иных условий проверяется на основе выдвижения соответствующих гипотез относительно 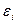. Оценочные значения 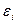определяются по формуле:

Для проверки условия 1 рассчитывается математическое ожидание - 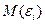по формуле:

.

Если данное выражение приблизительно равно нулю, то условие 1 выполняется.

Для проверки условия 2 рассчитывают величину F по формуле:

Далее по таблице распределения Фишера находим F_табл для степеней свободы и (n -количество наблюдений). Например, для 10 наблюдений и вероятности 95% F_табл = 6,39.

Если , то можно считать, что дисперсия постоянна (наблюдается гомоскедастичность). При более грубом подходе можно считать, что дисперсия постоянна, если 1/ F_табл<F_расч<F_табл. Если F_расч>F_табл, то дисперсия уменьшается, если 1/ F_табл>F_расч - дисперсия растет (наблюдается гетероскедастичность).

Нарушение условия 3 проявляется в том, что между ошибками разных наблюдений есть какая-то зависимость. Для проверки условия 3 рассчитывают критерий Дарбина-Уотсона по следующей формуле:

.

Нарушение условия независимости остатков между собой называется автокорреляцией остатков. По таблице распределения Дарбина-Уотсона определяется табличные значения d₁ и d₂ (приложение 3). Сравнивая D-W_расч с d₁ и d₂ можно проверить выполнение условия 3. В частности, если:

1) , то гипотеза об отсутствии автокорреляции отвергается;

2) 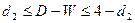, то гипотеза об отсутствии автокорреляции принимается;

3) , то принимается гипотеза о наличии отрицательной автокорреляции;

4) , то гипотезы не принимаются и не отвергаются (неопределенный случай).

Экономический смысл коэффициентов регрессии.

Необходимо на основе полученного регрессионного уравнения рассчитать на сколько изменится результат (значение переменной y) при изменении фактора (значения переменной x) на единицу. Данное изменение и является экономическим смыслом коэффициента регрессии (b).

Прогнозирование на основе полученной модели. Доверительный интервал прогноза.

После получения адекватного регрессионного уравнения прогнозирование осуществляется путем подстановки в регрессионное уравнение прогнозного значения независимой переменной (x), то есть прогнозное значение (у) определяется как функция:

y_{прогноз}=f(x_{прогноз}), т.е. как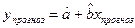

Надежность прогноза сводится к проблеме построения доверительного интервала прогноза. Построение доверительного интервала прогноза для однофакторного уравнения опирается на оценку дисперсии ошибки прогноза.

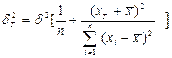
где – значение независимой переменной, для которого определяется прогноз;

- остаточная дисперсия регрессионного уравнения;

Используя необходимо построить доверительный интервал для истинного значения прогноза с заданной вероятностью p. Для этого рассчитывается величина t по формуле:

, которая подчиняется t- распределению с n-2 степенями свободы. Отсюда с заданной вероятностью величина t находится в интервале:

Отсюда интервал для истинного значения прогноза определяется как:

Выводы

Сформулируйте основные выводы проделанных расчетов: какую модель оценили, адекватна ли данная модель, какие показатели адекватности рассчитали и о чем они свидетельствуют, как можно использовать данную модель в экономическом анализе и прогнозе и т.д.

Приложение 1. F-распределение (распределение Фишера)

n1	n2
	18,51 98,5	19,0 99,0	19,16 99,17	19,25 99,25	19,3 99,3	19,33 99,33
	10,13 34,12	9,55 30,82	9,28 29,46	9,12 28,71	9,01 28,24	8,94 27,91
	7,71 21,2	6,94 18,0	6,59 16,69	6,39 15,98	6,26 15,52	6,16 15,21
	6,61 16,26	5,79 13,27	5,41 12,06	5,19 11,39	5,05 10,97	4,95 10,67
	5,99 13,74	5,14 10,92	4,76 9,78	4,53 9,15	4,39 8,75	4,28 8,47
	5,59 12,25	4,74 9,55	4,35 8,45	4,12 7,85	3,97 7,46	3,87 7,19
	5,32 11,26	4,46 8,63	4,07 7,59	3,84 7,01	3,69 6,63	3,58 6,37
	5,12 10,56	4,26 8,02	3,86 6,99	3,63 6,42	3,48 6,06	3,37 5,8
	4,96 10,04	4,1 7,56	3,71 6,55	3,48 5,99	3,33 5,64	3,22 5,39
	4,84 9,65	3,98 7,21	3,59 6,22	3,36 5,67	3,2 5,32	3,09 5,07
	4,75 9,33	3,89 6,93	3,49 5,95	3,26 5,41	3,11 5,06	3,0 4,82

Обычный шрифт для вероятности 95%, жирный - для 99%.

Приложение 2. t-распределение (распределение Стьюдента)

n	Вероятность
0,90	0,95	0,99
	6,314	12,706	63,657
	2,920	4,303	9,925
	2,353	3,182	5,841
	2,132	2,776	4,604
	2,015	2,571	4,032
	1,943	2,447	3,707
	1,895	2,365	3,499
	1,860	2,306	3,355
	1,833	2,262	3,250
	1,812	2,228	3,169
	1,782	2,179	3,055
	1,761	2,145	2,977

 

Приложение 3. D-W-распределение (распределение Дарбина-Уотсона)

N	k=1	k=2	k=3	k=4	k=5
d1	d2	d1	d2	d1	d2	d1	d2	d1	d2
	0,95	1,23	0,83	1,40	0,71	1,61	0,59	1,84	0,48	2,09
	1,08	1,28	0,99	1,41	0,89	1,55	0,79	1,70	0,70	1,87
	1,25	1,38	1,18	1,46	1,12	1,54	1,05	1,63	0,98	1,73
	1,42	1,50	1,38	1,54	1,34	1,59	1,30	1,64	1,26	1,69
	1,59	1,63	1,57	1,65	1,55	1,67	1,53	1,70	1,51	1,72

k – количество факторов, n – количество наблюдений.

Список рекомендуемой литературы:

1. Саяпова А.Р. Экономико-математические методы: Уч. пособие / БашГУ. –Уфа, 1995. 118 с.

2. Эконометрика: Учебник / Под. ред. Елисеевой И.И. – М.: Финансы и статистика, 2002. – 344 с.

3. Эконометрика: Учебник для вузов / Под ред. Кремера Н.Ш. – М.: ЮНИТИ-ДАНА, 2002. – 311 с.

4. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс: Уч. пособие. – М.: Дело, 1998 – 248 с.

5. Экономико-математические методы и прикладные модели: Уч. пособие / Под. ред. Федосеева В.В. – М.: ЮНИТИ, 1999. – 391 с.

 

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: